ABAQUS 中的一些约定

目录

• 自由度notation
  • Axisymmetric elements
  • Activation of degrees of freedom
  • Internal variables in Abaqus/Standard
• Coordinate systems
• Symbols used in Abaqus for units
• Time measures
• Convention used for stress and strain components
  • Nonisotropic material behavior
  • Zero-valued stress components
  • Shear strains
• 参考资料

自由度notation

除轴对称元件和电磁元件外,自由度通常表示为:

1 ---> x-displacement
2 ---> y-displacement
3 ---> z-displacement
4 ---> Rotation about the x-axis, in radians
5 ---> Rotation about the y-axis, in radians
6 ---> Rotation about the z-axis, in radians
7 ---> Warping amplitude (for open-section beam elements)
8 ---> Pore pressure, hydrostatic fluid pressure, or acoustic pressure
9 ---> Electric potential
10 ---> Connector material flow (units of length)
11 ---> Temperature (or normalized concentration in mass diffusion analysis)
12 ---> Second temperature (for shells or beams)
13 ---> Third temperature (for shells or beams)
14 ---> Etc.

Here the x-, y-, and z-directions coincide with the global X-, Y-, and Z-directions, respectively; however, if a local transformation is defined at a node (see Transformed coordinate systems), they coincide with the local directions defined by the transformation.

A maximum of 20 temperature values (degrees of freedom 11 through 30) can be defined for shell or beam elements in Abaqus/Standard.

Axisymmetric elements

轴对称单元的位移和转动自由度表示为:

1 ---> r-displacement
2 ---> z-displacement
5 ---> Rotation about the z-axis (for axisymmetric elements with twist), in radians
6 ---> Rotation in the r–z plane (for axisymmetric shells), in radians

这里的r和z方向分别与全局的X和y方向重合;然而,如果在节点上定义了局部转换(请参阅转换坐标系统),则它们与转换定义的局部方向一致.

Activation of degrees of freedom

Abaqus/Standard and Abaqus/Explicit activate only those degrees of freedom needed at a node. Thus, some of the degrees of freedom listed above may not be used at all nodes in a model, because each element type uses only those degrees of freedom that are relevant. For example, two-dimensional solid (continuum) stress/displacement elements use only degrees of freedom 1 and 2. The degrees of freedom actually used at any node are the envelope of those needed in each element that shares the node.

Internal variables in Abaqus/Standard

In addition to the degrees of freedom listed above, Abaqus/Standard uses internal variables (such as Lagrange multipliers to impose constraints) for some elements. Normally you need not be concerned with these variables, but they may appear in error and warning messages and are checked for satisfaction of nonlinear constraints during iteration. Internal variables are always associated with internal nodes, which have negative numbers to distinguish them from user-defined nodes.

Coordinate systems

Abaqus中默认的基本坐标系是右手直角笛卡尔坐标系.也可以自定义其他坐标系,但必须满足右手定则.

参见:坐标系说明

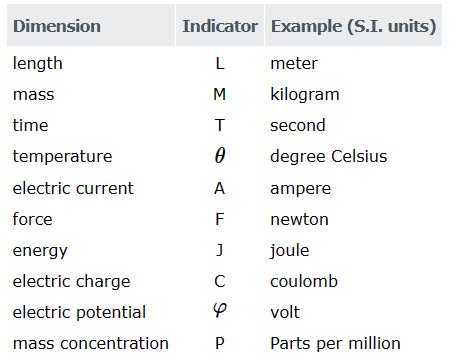
Symbols used in Abaqus for units

Time measures

Abaqus有两个时间:

• 分析步长时间
• 总时间.

除某些 linear perturbation procedures外,分析步时间从每一step的开始算.总时间从0开始,是所有 general analysis steps 累积的总时间( including restart steps).在线性扰动步骤中,总时间不累积.

Convention used for stress and strain components

在定义材料属性时,Abaqus中应力和应变分量的约定是排序:

σ11 --> Direct stress in the 1-direction
σ22 --> Direct stress in the 2-direction
σ33 --> Direct stress in the 3-direction
τ12 --> Shear stress in the 1–2 plane
τ13 --> Shear stress in the 1–3 plane
τ23 --> Shear stress in the 2–3 plane

例如,对于一个fully anisotropic, linear elasticity matrix:

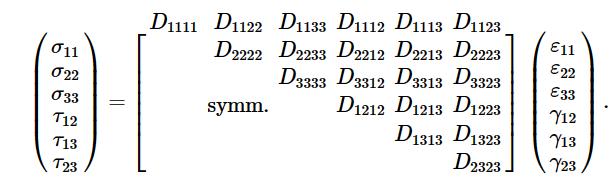
1-、2-和3-方向取决于所选择的元素类型.对于实体元素,这些方向的默认值是全局空间方向.对于壳和膜元素,默认的1-和2-方向是壳或膜表面的局部方向,as defined in About the element library.

在这两种情况下,1-、2-和3-方向都可以改变,as described in Orientations.

For geometrically nonlinear analysis with solid elements, the default (global) directions do not rotate with the material. However, user-defined orientations do rotate with the material.

Abaqus/Explicit stores the stress and strain components internally in a different order: σ11, σ22, σ33, τ12, τ23, τ13.

For geometrically nonlinear analysis, the internally stored components rotate with the material, regardless of whether or not a user-defined orientation is used. This distinction is important when a user subroutine (such as VUMAT) is used.

Nonisotropic material behavior

When nonisotropic material behavior is defined in continuum elements, a user-defined orientation is necessary for the anisotropic behavior to be associated with material directions. See State storage for a description of how material directions rotate.

Zero-valued stress components

Stress components that are always zero are omitted from storage. For example, in plane stress Abaqus stores only the two direct components and one shear component of stress and strain in the plane where the stress values are nonzero.

Shear strains

Abaqus always reports shear strain as engineering shear strain, γ :
γij = εij +εji .

---

参考资料

• 转换坐标系统; Transformed coordinate systems
• Boundary conditions # Prescribing boundary conditions in a time-harmonic eddy current analysis
• Boundary conditions