Abaqus压电材料分析

目录

• 1. ABAQUS压电材料定义【快速版】
• 2. 压电材料的主要特性参数
• 3. Abaqus 压电分析
  • 1 电响应
  • 2 initial condition & BCs
  • 4 Load
  • 5 Material options & Elements
  • outputs
• 4 压电夹层结构的abaqus建模
• 5. 压电Damper原理
• 6. 压电的文献笔记
  • 文献一:
    • 摘要:
    • 主要工作:
    • 研究方法:
    • 研究流程:
    • 结论:
  • 文献二:
    • 摘要:
    • 主要工作:
    • 研究方法:
    • 研究流程:
    • 结论:
  • <压电层合板等效单层Mindlin理论及其应用>
    • 摘要提取:
    • 论文中心精炼:
    • 论文做了什么工作?
    • 研究方法:
    • 研究流程:
    • 验证案例:
    • 条件设定:
    • 验证结论:
• 7. 压电夹层在螺旋桨中的阻尼计算(能量计算)设想20240908
  • 四类压电方程

1. ABAQUS压电材料定义【快速版】

• 压电本构方程:

压电材料行为定义所需:

• 密度(optional)
• 线弹性-刚度矩阵(S_ijkl or D_ijkl)
• Piezoelectric-压电应变常数矩阵
• Dielectric(electric permittivity)-介电常数矩阵

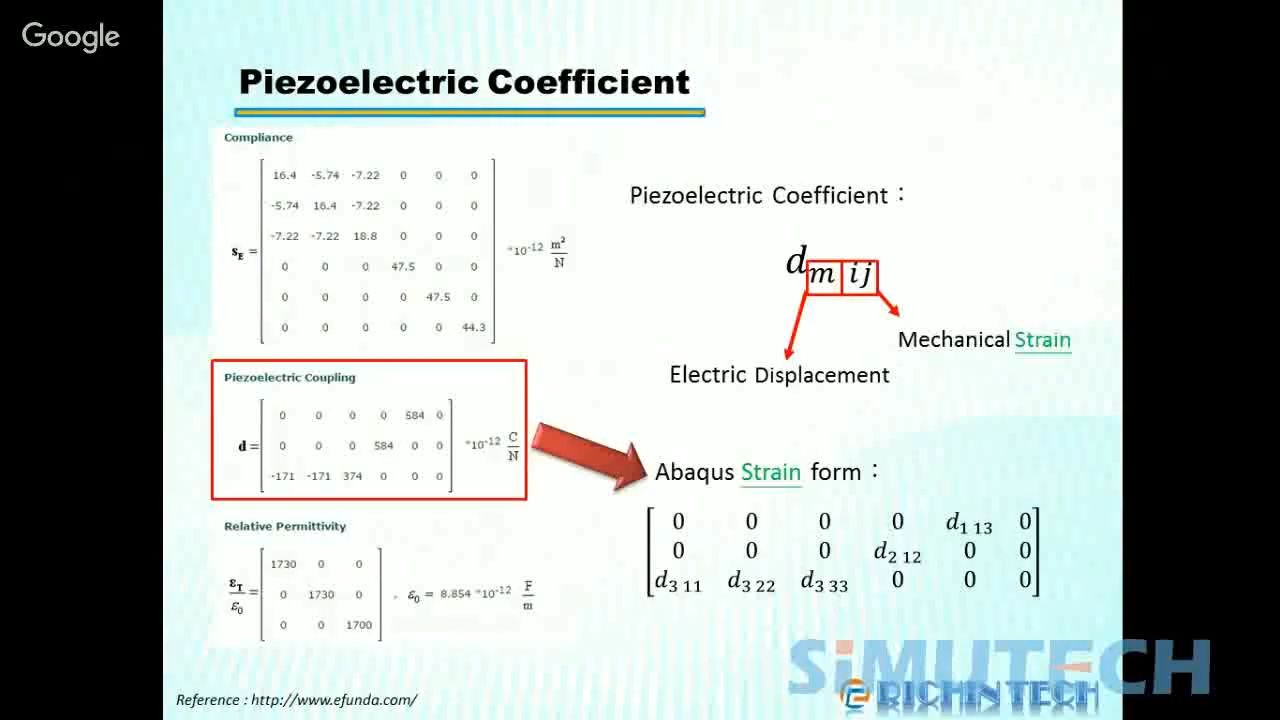
其中压电应变常数矩阵和介电常数矩阵的独立变量为:

1. d31=d32,d33,d24=d15
2. \(\epsilon11=\epsilon22,\epsilon33\)

• 定义压电材料的材料方向

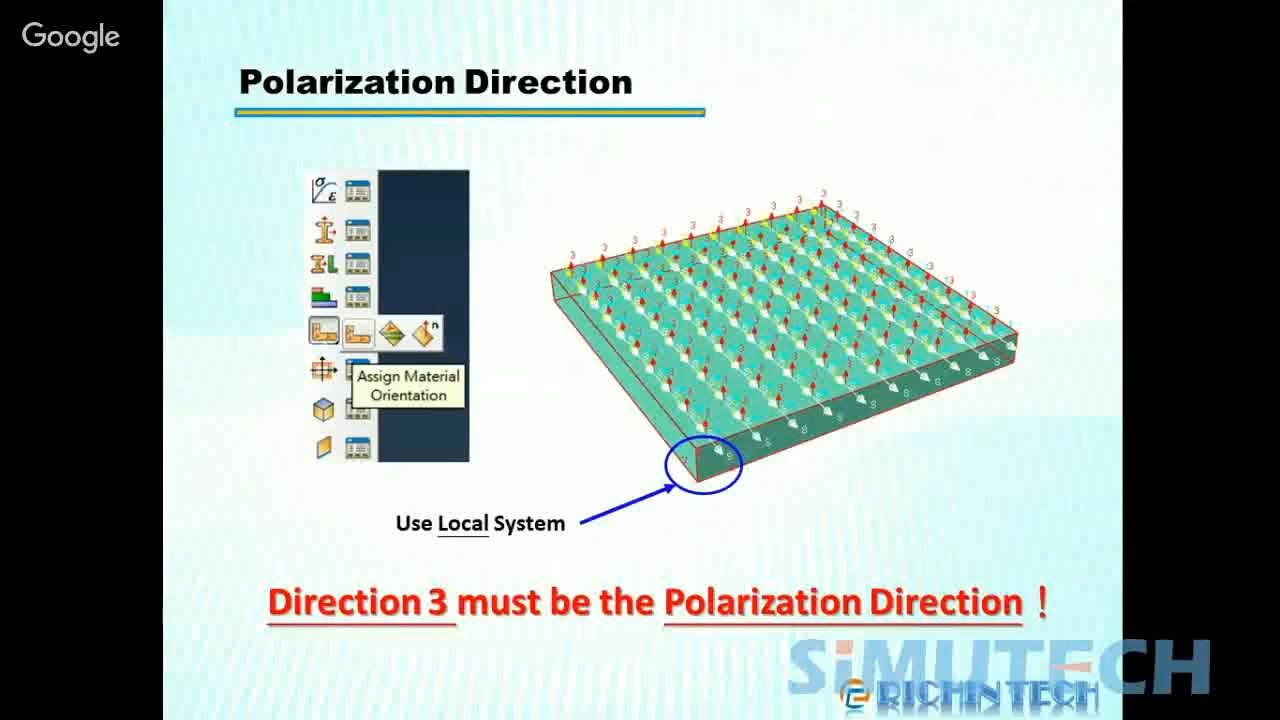
由于压电材料具有极化方向,因此需要创建一个局部坐标系,赋予material orientation 时,必须确保3-方向为极化方向

• 单元类型和输出

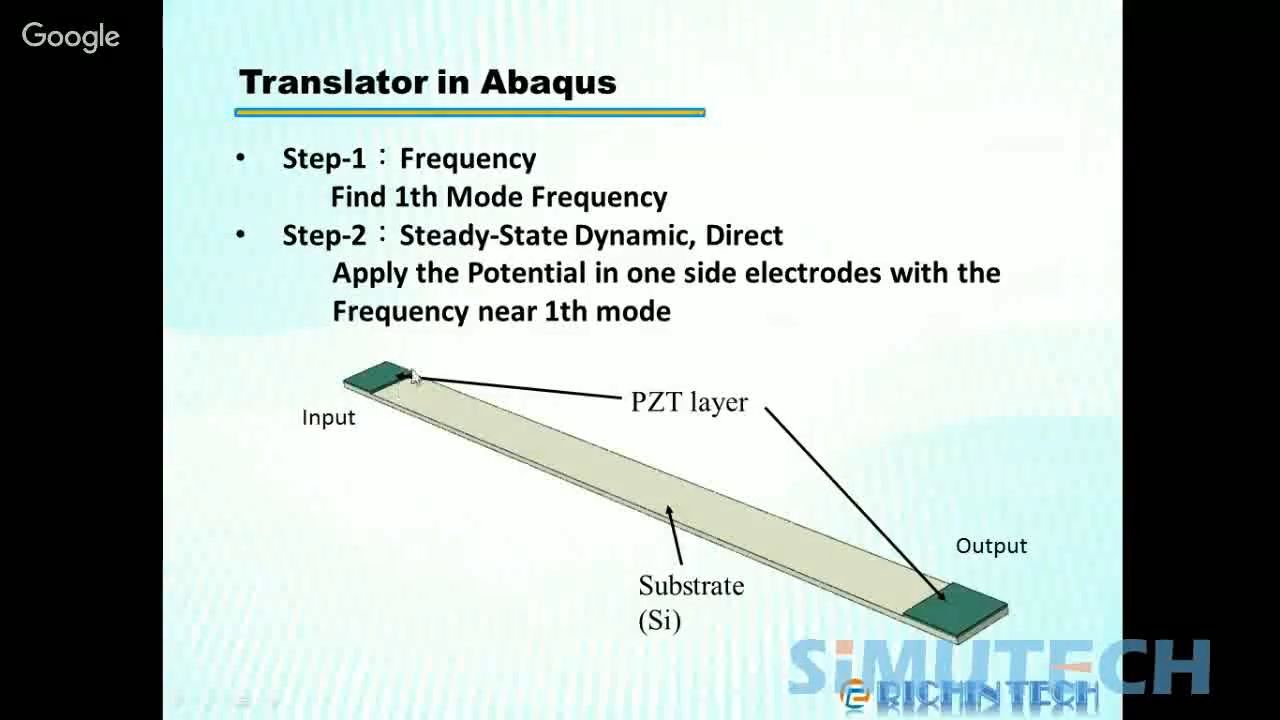
常用的单元类类型:

• HEX: C3D8E,C3D20(R)E
• TET: C3D4E,C3D10E

节点自由度:1 2 3 9(电压)

EX1:

施加应力,产生电位移和电场强度,该强度在内部会产生应变来抵抗加载.

EX2

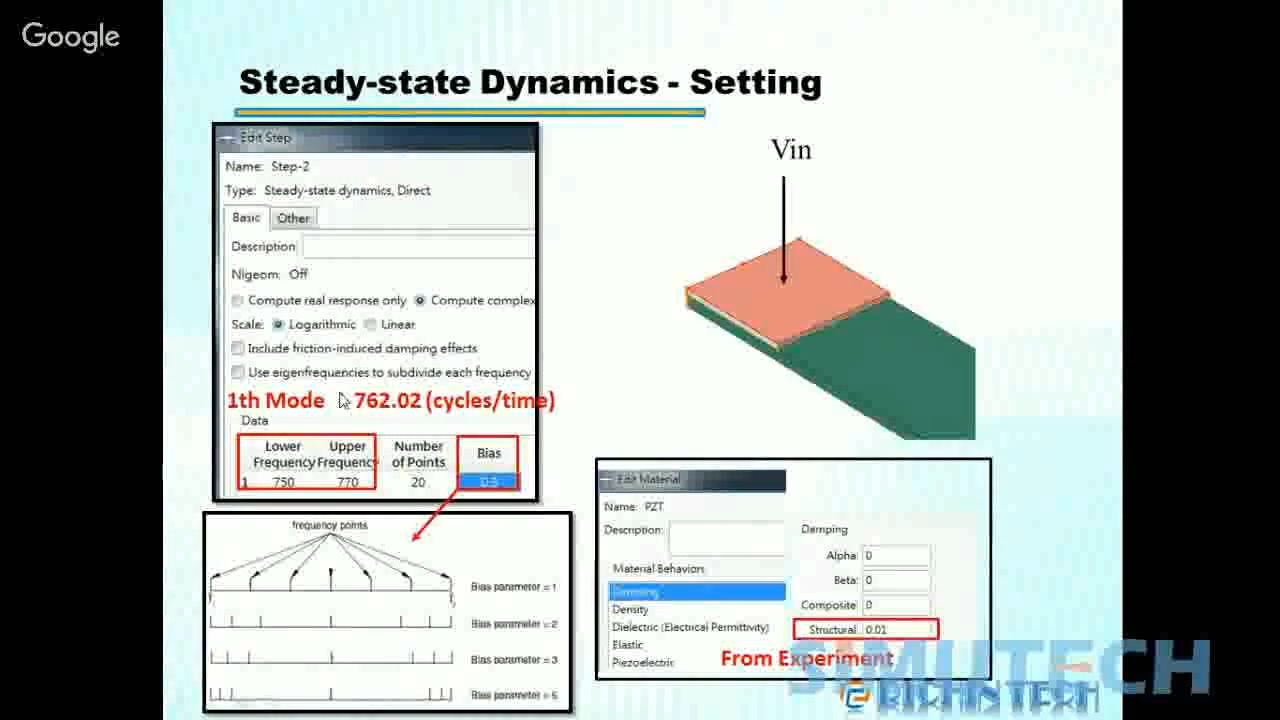
2. 压电材料的主要特性参数

• 压电常数: 压电常数是衡量材料压电效应强弱的参数,它直接关系到压电输出的灵敏度.
• 弹性常数: 压电材料的弹性常数、刚度决定着压电器件的固有频率和动态特性.
• 介电常数: 对于一定形状、尺寸的压电元件,其固有电容与介电常数有关;而固有电容又影响着压电传感器的频率下限.
• 机械耦合系数: 在压电效应中,其值等于转换输出能量(如电能)与输入的能量(如机械能)之比的平方根;它是衡量压电材料机电能量转换效率的一个重要参数.
• 电阻压电材料的绝缘电阻: 将减少电荷泄漏,从而改善压电传感器的低频特性.
• 居里点: 压电材料开始丧失压电特性的温度称为居里点.

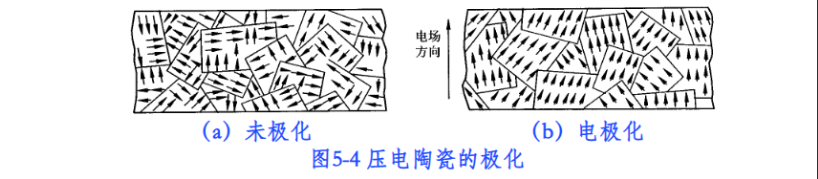
当陶瓷材料受到外力作用时,电畴的界限发生移动,电畴发生偏转,从而引起剩余极化强度的变化,因而在垂直于极化方向的平面上将出现极化电荷的变化.这种因受力而产生的由机械效应转变为电效应,将机械能转变为电能的现象,就是压电陶瓷的正压电效应.电荷量的大小与外力成正比关系:

\[\begin{gather} Q=d_{33}F \\ d_{33}:压电常数 \\ F=作用力 \end{gather} \]

3. Abaqus 压电分析

参考自:abaqus帮助文档-压电分析

Coupled piezoelectric problems:

• are those in which an electric potential gradient causes straining, while stress causes an electric potential gradient in the material;
• are solved using an eigenfrequency extraction, modal dynamic, static, dynamic, or steady-state dynamic procedure;
• require the use of piezoelectric elements and piezoelectric material properties;
• can be performed for continuum problems in one, two, and three dimensions; and
• can be used in both linear and nonlinear analysis (however, in nonlinear analysis the piezoelectric part of the constitutive behavior is assumed to be linear).

压电分析可以通过以下程序进行:

• Static Stress Analysis

• Implicit Dynamic Analysis Using Direct Integration

• Direct-Solution Steady-State Dynamic Analysis

• Natural Frequency Extraction

• Transient Modal Dynamic Analysis

• Mode-Based Steady-State Dynamic Analysis

• Subspace-Based Steady-State Dynamic Analysis

1 电响应

压电材料的电学响应=介电效应+压电效应:

\[\begin{array}{c} {{q_{i}=e_{i j k}^{\varphi}\varepsilon_{j k}+D_{i j}^{\varphi}}E_{j}} \end{array} \]

• \(q_i=[q1,q2, q3]^{T}\):电位移(i-direction)
• \(\varphi\):电势
• \(e^{\varphi}_{ijk}\):压电应力耦合矩阵
• \(\epsilon_{ij}\):应变分量
• \(D^{\varphi(\epsilon)}_{ij}\):介电常数矩阵
• \(E_{j}=-\frac{\partial \varphi}{\partial x_i}\):电势梯度,即电场强度

2 initial condition & BCs

关于电变量的initial condition 不能指定.

abaqus的节点自由度9为电势(electric potential).在eigenfrequency Extract step中,如果用到了压电单元,则必须至少约束住一个节点的电势自由度.

用于消除单元算子的奇异性

4 Load

可用于压电分析的Loads:

1. Mechanical Loads
   1. 集中节点力
   2. 分布压力
   3. 体积力
2. Electrical Loads
   1. 集中电荷
   2. 分布面电荷
   3. 体电荷

Loading in Mode-Based and Subspace-Based Procedures:

1. 电荷负载只能与eigenfrequency Extract step的residual mode 结合使用.电势自由度因为无相关质量,在计算过程中相关自由度会被消除.

The residual modes represent the static response corresponding to the electrical charge loads, which will adequately represent the potential degree of freedom in the eigenspace.

5 Material options & Elements

• Material options

1. 压电耦合矩阵、介电耦合矩阵可以联合定义"压电的电响应行为";
2. 力学行为部分只能包括线弹性;
3. 对于压电材料可以定义压电阻尼(*PIEZOELECTRIC DAMPING),它不同于材料阻尼(*Damping):
   1. 与刚度成比例的粘性阻尼 : *PIEZOELECTRIC DAMPING, BETA
   2. 与刚度成比例的结构阻尼 : PIEZOELECTRIC DAMPING, STRUCTURAL

Piezoelectric damping is not supported in Abaqus/CAE.

• Elements

Piezoelectric elements must be used in a piezoelectric analysis. The electric potential, \(\varphi\), is degree of freedom 9 at each node of these elements.

In addition, regular stress/displacement elements can be used in parts of the model where piezoelectric effects do not need to be considered.

outputs

• 积分点var
  • EENER:静电能密度
  • EPG=\(- \frac{\partial \varphi}{\partial x_i}\):电势梯度向量的负值
  • EFLX:电通量(位移)矢量,q_i,i=1 2 3
• whole elem var:
  • CHRGS:分布电荷值
  • ELCTE:单元内的总静电能.$\int_{V}EENER dV $
• nodal var:
  • EPOT:节点的电势值
  • CECHG:集中节点电荷
  • RCHG:反应的节点电荷

4 压电夹层结构的abaqus建模

物理结构:

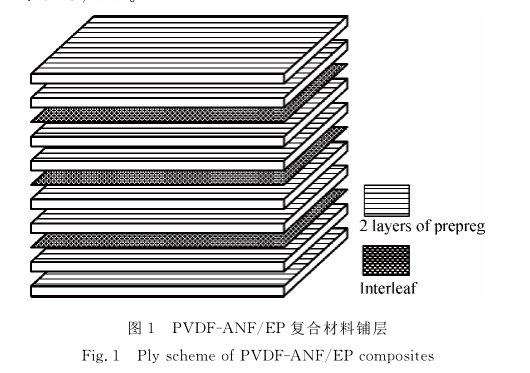
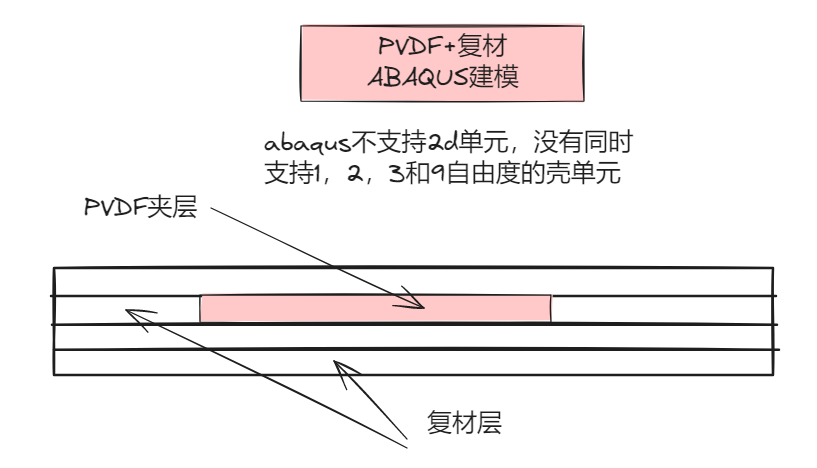
有限元建模:

5. 压电Damper原理

Piezoelectric Composite Materials - ScienceDirect

当振动传递到压电材料时,振动能量通过压电效应转化为电能,产生交流电压.所产生的电能\(U_E\)可以用机电耦合系数k和机械能\(U_m\)表示:

\[U_\mathrm{E}=U_\mathrm{M}\times k^2 \]

• 电路处于开路或者短路

电能又会重新转换为振动能(不存在能量损耗)

• 接上电阻

部分电能以电阻焦耳热的形式耗散,可以迅速抑制振动.

graph LR A[振动能]--压电效应-->B[交流电流产生] B---->C[电阻发热] B--随着应变变小而有部分电能转换回应变能-->A

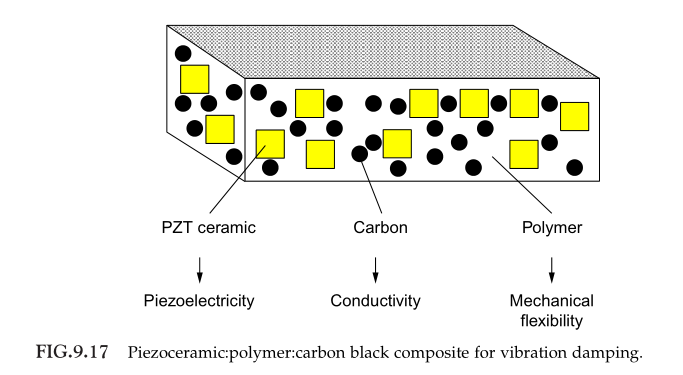
下图是用于减震的｛压电陶瓷-聚合物-炭黑｝复合材料

上图来源:A new vibration damping CFRP material with interlayers of dispersed piezoelectric ceramic particles - ScienceDirect

6. 压电的文献笔记

文献一:

摘要:

本文利用双向压电-机械耦合理论来研究具有表面粘贴压电致动器和传感器的复合材料层合板的多场相互作用.采用高阶电位场以准确描述压电层中电位的非均匀分布,并使用高阶层合板理论来描述复合材料层合板和压电层的位移场,以准确模拟在中等厚度结构中显著的横向剪切变形.开发了有限元层合板模型,用以实现理论,并研究了致动和传感效应.

主要工作:

• 建立双向压电-机械耦合理论
• 开发有限元层合板模型
• 研究压电材料的致动和传感效果

研究方法:

• 使用高阶电位场和位移场理论
• 基于耦合场的变分原理获取控制方程
• 利用有限元技术实现理论

研究流程:

1. 引入高阶电位场和位移场假设
2. 根据变分原理建立控制方程
3. 通过有限元方法求解控制方程
4. 分析耦合效应对结构变形、应力分布和电信号预测的影响
5. 比较耦合模型与非耦合模型的结果

结论:

• 双向耦合效应显著影响结构变形、应力分布和电信号的预测
• 压电层与板结构的厚度比是控制耦合效应重要性的一个关键参数
• 耦合理论能够准确模拟厚压电层的特性
• 非耦合模型在预测电荷积累和电场分布方面存在偏差

文献二:

摘要:

本文提出了一种简单的有限元公式,用于分析带有层状压电层的复合板.基于经典层合板理论和电磁耦合激励,利用变分原理,为基于均匀化数值积分和沙漏稳定的Mindlin板元素制定了运动方程.

主要工作:

• 提出一种用于分析带有压电层的层合板的简化有限元公式
• 利用经典层合板理论和变分原理制定运动方程
  - 使用四节点、24自由度的矩形壳元素进行离散化

研究方法:

• 基于经典层合板理论
• 引入电磁耦合激励
• 使用变分原理
• 应用数值积分和沙漏稳定技术

研究流程:

1. 选择四节点、双线性位移Mindlin板元素
2. 利用Hamilton原理推导层合板的运动方程
3. 引入沙漏稳定技术处理数值积分问题
4. 通过实验和文献中的分析结果验证有限元公式的性能

结论:

• 提出的有限元模型与实验数据和文献中的固体元素公式结果吻合良好
• 基于一点积分Mindlin板公式的有限元模型比固体元素模型更简单、计算效率更高
• 该模型在模拟问题时使用的自由度数量显著减少,降低了计算内存和时间需求

<压电层合板等效单层Mindlin理论及其应用>

Equivalent single‐layer Mindlin theory of laminated piezoelectric plates and application - Lian - 2024 - ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik - Wiley Online Library

摘要提取:

本文基于Mindlin一阶剪切变形理论,提出了一种等效单层(ESL)板理论来分析层状压电板(LPPs)的电-力耦合问题.主要特点包括:

• (i) 假设电势沿厚度方向是多项式函数,确保其在界面的连续性;
• (ii) 电位移在界面连续,符合层压板界面连续性条件.

得到了LPPs变形和电势的理论解.通过与三维有限元方法(FEM)得到的双层和四层LPPs结果的比较,验证了理论解的有效性和准确性.数值结果讨论了不同级数展开的影响,并强调了高阶展开的必要性.同时,讨论了三维FEM的适用范围.期望这种新的分析方法能为压电器件的优化设计提供指导.

![[240727-PVDF &阻尼&有限元建模-3.png]]

论文中心精炼:

论文的中心是提出并验证一种新的理论模型_等效单层Mindlin理论,用于分析层状压电板的电-力耦合问题,特别是针对微/纳尺度的层状压电板.

论文推导的等效公式,针对含多种压电材料的多层结构进行等效

论文做了什么工作?

• 提出了基于Mindlin一阶剪切变形理论的等效单层(ESL)板理论.
• 建立了电势沿厚度方向的多项式函数表达,确保电势在层间界面的连续性.
• 推导出了电位移的连续性条件,满足层压板的界面连续性要求.
• 获得了LPPs的变形和电势的理论解.
• 通过与三维有限元方法(FEM)结果的比较,验证了新理论的有效性和准确性.

论文推导了LPPs的等效本构方程:

\[\sigma_{ij}=\bar{c}_{ijkl}\varepsilon_{kl}-\alpha\bar{e}_{ijk}E_{k}\quad D_{i}=\alpha\bar{e}_{ikl}\varepsilon_{kl}+\bar{\kappa}_{ik}E_{k},\\ \]

式中:

\[\begin{gathered} \bar{c}_{ijkl} =c_{ijkl}-c_{ij33}c_{33kl}/c_{3333}, \\ \bar{e}_{kij} =e_{kij}-e_{k33}c_{33ij}/c_{3333}, \\ \bar{\kappa}_{ij} =\kappa_{ij}-e_{i33}e_{j33}/c_{3333}. \end{gathered}\]

研究方法:

• 利用Mindlin一阶剪切变形理论,构建了ESL理论框架.
• 采用多项式函数来描述电势沿厚度方向的分布.
• 引入了电位移的连续性条件,确保了理论模型满足物理实际.
• 通过数学推导,建立了电-力耦合的控制方程.
• 使用三维有限元方法(FEM)作为参考解,对新理论进行验证.

研究流程:

1. 理论构建:基于Mindlin理论,提出ESL板理论.
2. 函数假设:假设电势为沿厚度方向的多项式函数.
3. 推导控制方程:建立电-力耦合的动力学和静电力学方程.
4. 求解方程:求解得到LPPs的变形和电势分布.
5. 结果验证:与三维FEM结果进行比较,验证理论解的准确性.
6. 参数影响分析:研究不同参数(如厚度-宽度比、材料组合)对电势分布的影响.
7. 结论提炼:根据研究结果,得出结论并讨论新理论的应用前景.

论文中包含了验证案例,具体如下:

验证案例:

1. 双层压电复合板:由PZT-5H/PZT4两种不同材料的均匀各向同性压电层组成,具有相同的厚度,沿z轴方向极化.板的尺寸和厚度具体为L1 = 3 µm, L2 = 3 µm, hI = 100 nm(I = 1, 2),厚度与宽度的比为h/L1 = 1/15.材料属性在表1中列出.假设板的上表面受到均匀分布的载荷q0.

2. 四层压电复合板:由PZT-4/PZT-5H/PZT7/PZT8材料组成,每种材料层的厚度相同,为hI = 100 nm(I = 1, 2, 3, 4),极化方向同样沿z轴.板的尺寸为L1 = 7.5 µm, L2 = 7.5 µm.同样受到均匀分布的载荷q0.

条件设定:

• 两种案例中,板的边界条件均为固定四周,即在边缘x = 0和L1,y = 0和L2处,分别设置了u(0)1, u(1)1, w, D(0)x和u(0)2, u(1)2, w, D(0)y的边界条件.
• 板的角落x = L1和y = 0处,设置了电势φ(0)的边界条件.
• 板的上下表面没有电极,因此引入了自然边界条件Dz = 0.

验证结论:

• 对于双层和四层压电复合板,ESL理论的结果与三维有限元方法(FEM)的结果进行了比较,显示出良好的一致性,特别是在板的中心区域.
• 在双层板案例中,电势的计算结果显示在板的中心位置变化最小,最大差异达到10%,这归因于挠度的低阶展开.
• 在四层板案例中,电势的ESL理论结果与三维FEM结果在板的上下表面非常接近,但在中间层的一致性较差,这可能归因于电势幂级数展开中的高阶项的贡献.
• 当板的厚度-宽度比hI/L1减小时,本文理论与三维FEM结果之间的差异增加.特别是对于hI/L1 = 1/80,甚至更薄的板,三维FEM结果出现不收敛,而ESL理论方法仍然适用并有效.
• 材料组合对电势分布有一定影响,不同材料组合下沿厚度方向的电势分布存在显著差异.

7. 压电夹层在螺旋桨中的阻尼计算(能量计算)设想20240908

用应变能法计算含有压电夹层的螺旋桨的阻尼因子,使用下面的公式:

来自https://doi.org/10.1016/j.compscitech.2006.08.022

对上述公式做一个分解:

\[\begin{align} \eta_{all} & = \frac{\eta_p E_p+\eta_c E_c}{E_p+E_c} \\ & = \eta_p \frac{ E_p +E_c -E_c}{E_p+E_c}+\frac{ \eta_c E_c}{E_p+E_c}\\ & = \eta_p+\frac{E_c}{E_p +E_c}(\eta_c-\eta_p)\\ \end{align} \]

其中:p,c,all分别表示pvdf,composite ,整体结构

如果取\(E_p\)为自变量,那么:

\[\begin{align} \eta_c > \eta_p , if \ E_p \Uparrow ,then \ \ \eta_{all} \Downarrow ;\\ \eta_c < \eta_p , if \ E_p \Uparrow ,then \ \ \eta_{all} \Uparrow ;\\ \end{align} \]

四类压电方程

---

• 压电陶瓷的压电系数 .
• https://zhidao.baidu.com/question/398538303.html .
• https://baike.baidu.com/item/压电系数/1670306 .
• https://baike.baidu.com/item/压电常数/9054614 .
• https://www.eefocus.com/baike/1517341.html#:~:text=压电系数的计算方法通常是将压电效应分析为线性矩阵表示，其中行向量对应于应变张量，列向量对应于,电场强度 张量，并将此矩阵乘以应变张量，从而得到电场强度张量。 .