【刚度矩阵推导】2d frame 单元
2d frame 单元是x-y平面上的单元,每个节点上有2个平移自由度的和一个转动自由度.局部坐标系下,单元位移向量为:
\( u=[ u_1 ,u_2 ,u_3, u_4, u_5, u_6]^{T} \)
其局部坐标系下的刚度矩阵可以由2d truss单元和2d bornoulli-beam单元的刚度矩阵组合而成.
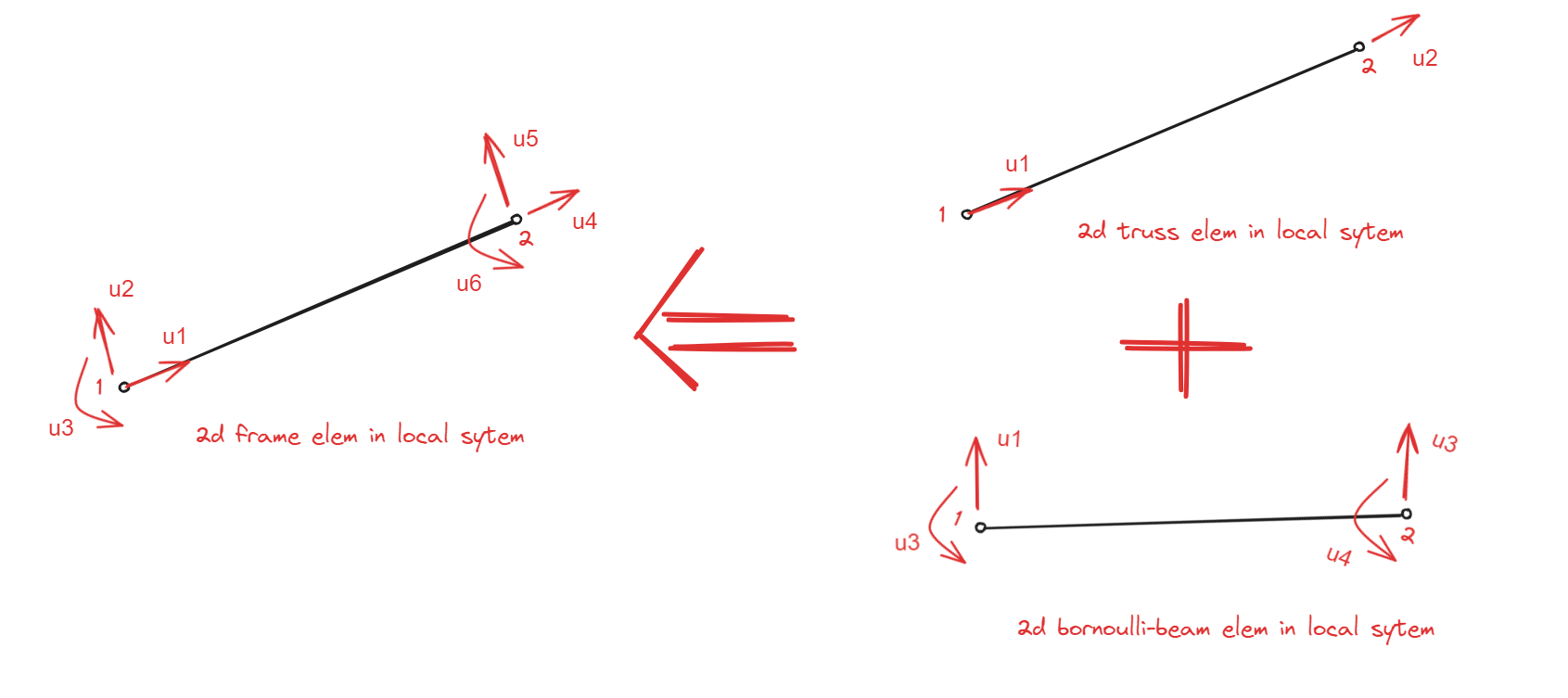
使用matlab进行推导:
% ! bornoulli-beam element stiffness matrix in local system
clc
clear
syms E Iz L A
a=0.5*L;
k_e_bornoulli_beam_stiffness=E*Iz/(2*a^3)*[3 3*a -3 3*a ;3*a 4*a*a -3*a 2*a*a; -3 -3*a 3 -3*a;3*a 2*a*a -3*a 4*a*a ];
disp('k_e_bornoulli_beam_stiffness:')
simplify(k_e_bornoulli_beam_stiffness)
% todo : 2d truss element stiffness matrix in local system
k_e_2d_truss_stiffness=(E*A/L)*[1 -1; -1 1];
% todo : elem's dof
frame_2d_stiffness=sym(zeros(6,6));
frame_2d_stiffness([1,4],[1,4])=k_e_2d_truss_stiffness;
frame_2d_stiffness([2,3,5,6],[2,3,5,6])=k_e_bornoulli_beam_stiffness;
disp('frame_2d_stiffness:')
simplify(frame_2d_stiffness)
<!-- 输出结果 -->
k_e_bornoulli_beam_stiffness:
[ (12*E*Iz)/L^3, (6*E*Iz)/L^2, -(12*E*Iz)/L^3, (6*E*Iz)/L^2]
[ (6*E*Iz)/L^2, (4*E*Iz)/L, -(6*E*Iz)/L^2, (2*E*Iz)/L]
[-(12*E*Iz)/L^3, -(6*E*Iz)/L^2, (12*E*Iz)/L^3, -(6*E*Iz)/L^2]
[ (6*E*Iz)/L^2, (2*E*Iz)/L, -(6*E*Iz)/L^2, (4*E*Iz)/L]
frame_2d_stiffness:
[ (A*E)/L, 0, 0, -(A*E)/L, 0, 0]
[ 0, (12*E*Iz)/L^3, (6*E*Iz)/L^2, 0, -(12*E*Iz)/L^3, (6*E*Iz)/L^2]
[ 0, (6*E*Iz)/L^2, (4*E*Iz)/L, 0, -(6*E*Iz)/L^2, (2*E*Iz)/L]
[-(A*E)/L, 0, 0, (A*E)/L, 0, 0]
[ 0, -(12*E*Iz)/L^3, -(6*E*Iz)/L^2, 0, (12*E*Iz)/L^3, -(6*E*Iz)/L^2]
[ 0, (6*E*Iz)/L^2, (2*E*Iz)/L, 0, -(6*E*Iz)/L^2, (4*E*Iz)/L]
本文来自博客园,作者:FE-有限元鹰,转载请注明原文链接:https://www.cnblogs.com/aksoam/p/18159778


 浙公网安备 33010602011771号
浙公网安备 33010602011771号