有限元方法[Matlab]-笔记
![有限元方法[Matlab]-笔记](https://img2024.cnblogs.com/blog/2026433/202408/2026433-20240805095548845-1104772374.png)
《 MATLAB Codes for Finite Element Analysis - Solids and Structures (Ferreira) 》 的学习笔记
<< MATLAB Codes for Finite Element Analysis - Solids and Structures (Ferreira) >> 笔记
目录
第一章:matlab基础
略
第二章: 离散系统
笔记、例题
Matlab代码
problem1.m
% MATLAB codes for Finite Element Analysis
% Problem 1: 3 springs problem
% clear memory
clear ;
% ? define vars
P=10; % N
ki=[1;1;1;1];
% elementNodes: connections at elements
elementNodes=[1 2;
2 3;
2 4];
% numberElements: number of Elements
numberElements=size(elementNodes,1);
% numberNodes: number of nodes
numberNodes=4;
% for structure:
% displacements: displacement vector N x 1
% force : force vector N x 1
% stiffness: stiffness matrix N x N
displacements=zeros(numberNodes,1); %#ok<PREALL>
force=zeros(numberNodes,1);
stiffness=zeros(numberNodes);
% applied load at node 2
force(2)=P;
% computation of the system stiffness matrix
for e=1:numberElements
% elementDof: element degrees of freedom (Dof)
elementDof=elementNodes(e,:) ;
stiffness(elementDof,elementDof)=...
stiffness(elementDof,elementDof)+ki(e)*[1 -1;-1 1];
end
% boundary conditions and solution
% prescribed dofs
prescribedDof=[1;3;4];
% free Dof : activeDof
% setdiff() 函数-->求两个数组的差集
% C = setdiff(A,B) 返回 A 中存在但 B 中不存在的数据,不包含重复项.C 是有序的.
activeDof=setdiff((1:numberNodes)',prescribedDof);
% solution
% !KU=F --> U=K\F
displacements=stiffness(activeDof,activeDof)\force(activeDof);
% positioning all displacements
displacements1=zeros(numberNodes,1);
displacements1(activeDof)=displacements;
% output displacements/reactions
outputDisplacementsReactions(displacements1,stiffness,numberNodes,prescribedDof)
outputDisplacementsReactions.m
function outputDisplacementsReactions(displacements,stiffness,GDof,prescribedDof)
% output of displacements and reactions in
% tabular form
% GDof: total number of degrees of freedom of the problem
% displacements
disp('Displacements')
%displacements=displacements1;
jj=1:GDof; % format
[jj' displacements]
% reactions
F=stiffness*displacements;
reactions=F(prescribedDof);
disp('reactions')
[prescribedDof reactions]
end
第三章:1D 杆单元
笔记
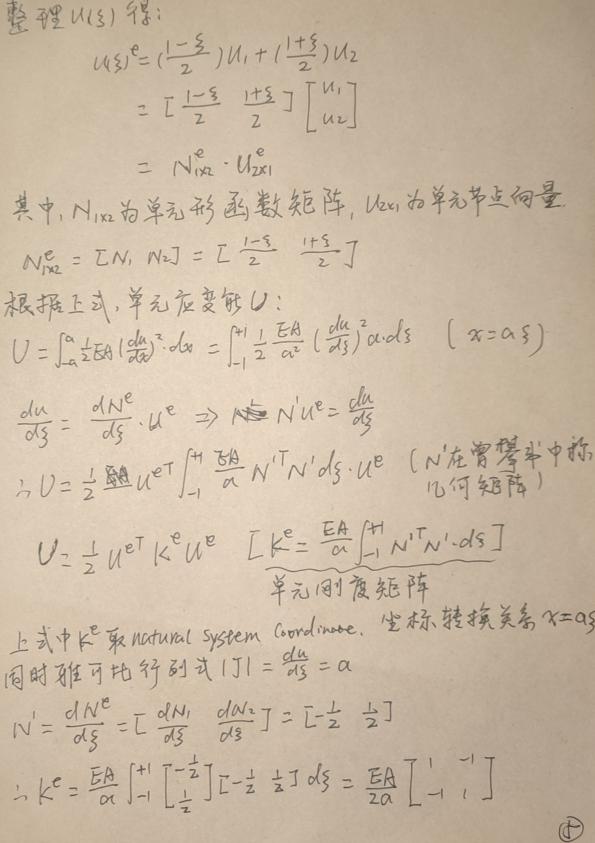
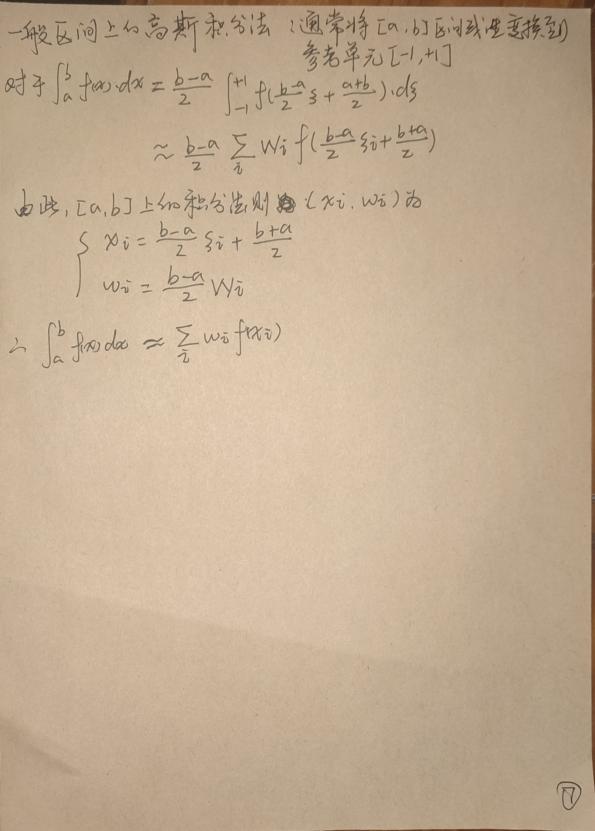
例题1
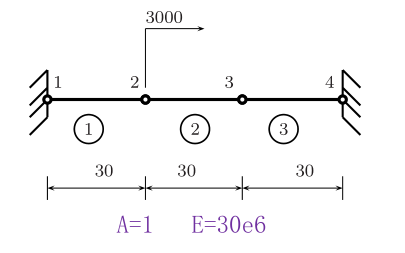
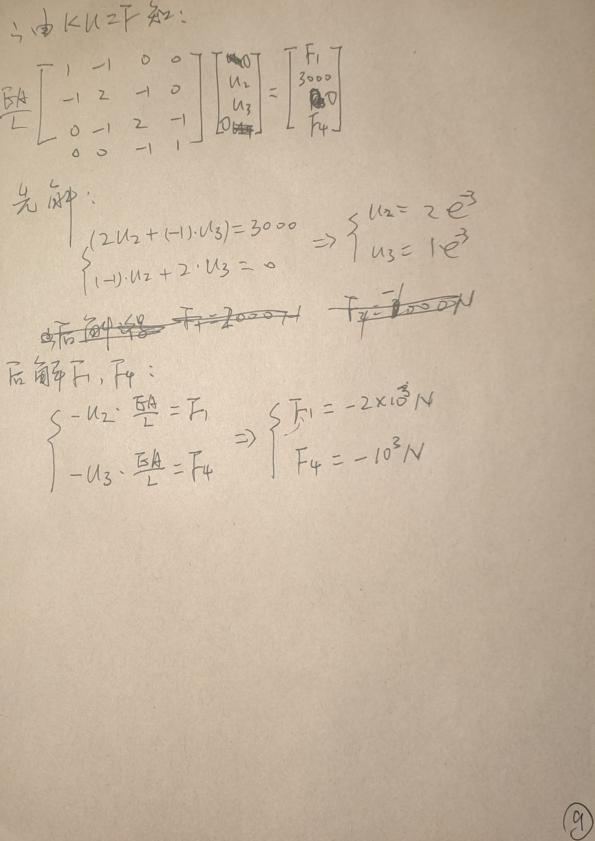
matlab 代码
problem2.m
% antonio ferreira 2008
% clear memory
clear all
% E; modulus of elasticity
% A: area of cross section
% L: length of bar
E = 30e6;A=1;EA=E*A; L = 90;
% generation of coordinates and connectivities
% numberElements: number of elements
numberElements=3;
% generation equal spaced coordinates
nodeCoordinates=linspace(0,L,numberElements+1);
xx=nodeCoordinates;
% numberNodes: number of nodes
numberNodes=size(nodeCoordinates,2);
% elementNodes: connections at elements
ii=1:numberElements;
elementNodes(:,1)=ii;
elementNodes(:,2)=ii+1;
% for structure:
% displacements: displacement vector
% force : force vector
% stiffness: stiffness matrix
displacements=zeros(numberNodes,1); %#ok<PREALL>
force=zeros(numberNodes,1);
stiffness=zeros(numberNodes,numberNodes);
% applied load at node 2
force(2)=3000.0;
% computation of the system stiffness matrix
for e=1:numberElements;
% elementDof: element degrees of freedom (Dof)
elementDof=elementNodes(e,:) ;
nn=length(elementDof);
length_element=nodeCoordinates(elementDof(2))...
-nodeCoordinates(elementDof(1));
detJacobian=length_element/2;invJacobian=1/detJacobian;
% central Gauss point (xi=0, weight W=2)
[shape,naturalDerivatives]=shapeFunctionL2(0.0);
Xderivatives=naturalDerivatives*invJacobian;
% B matrix
B=zeros(1,nn); B(1:nn) = Xderivatives(:);
stiffness(elementDof,elementDof)=stiffness(elementDof,elementDof)+B'*B*2*detJacobian*EA;
end
% boundary conditions and solution
% prescribed dofs
fixedDof=find(xx==min(nodeCoordinates(:)) | xx==max(nodeCoordinates(:)))';
prescribedDof=[fixedDof]
% free Dof : activeDof
activeDof=setdiff([1:numberNodes]',[prescribedDof]);
% solution
GDof=numberNodes;
displacements=solution(GDof,prescribedDof,stiffness,force);
% output displacements/reactions
outputDisplacementsReactions(displacements,stiffness,numberNodes,prescribedDof)
disp(stiffness)
disp(force)
disp(displacements)
solution.m
function displacements=solution(GDof,prescribedDof,stiffness,force)
% function to find solution in terms of global displacements
activeDof=setdiff([1:GDof]', ...
[prescribedDof]);
U=stiffness(activeDof,activeDof)\force(activeDof);
displacements=zeros(GDof,1);
displacements(activeDof)=U;
end
shapeFunctionL2.m
function [shape,naturalDerivatives]=shapeFunctionL2(xi)
% shape function and derivatives for L2 elements
% shape : Shape functions
% naturalDerivatives: derivatives w.r.t. xi
% xi: natural coordinates (-1 ... +1)
shape=([1-xi,1+xi]/2)';
naturalDerivatives=[-1;1]/2;
end
例题2
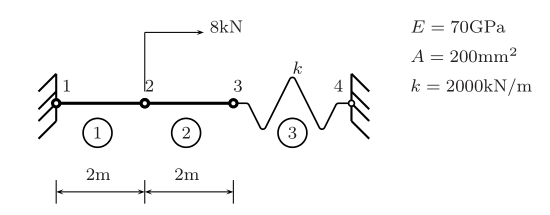
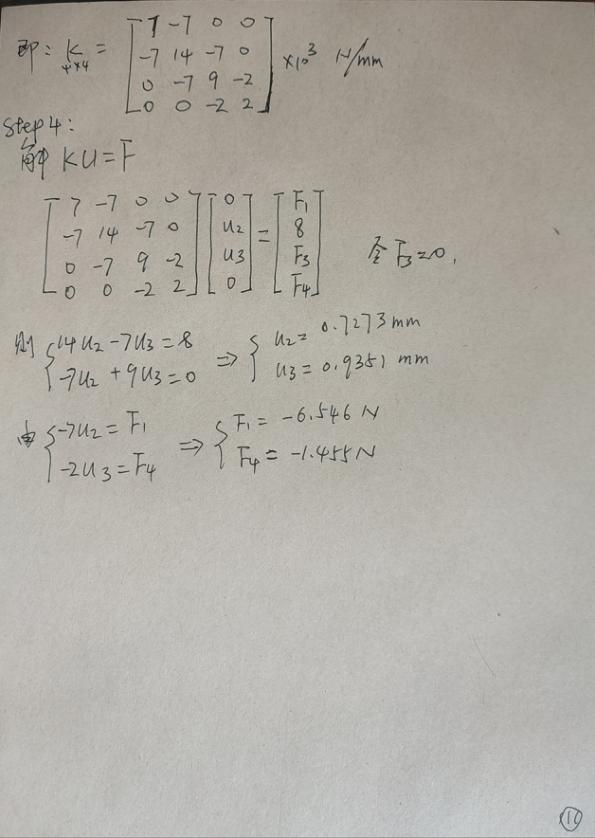
matlab 代码
problem3Structure.m
% MATLAB codes for Finite Element Analysis
% antonio ferreira 2008
% clear memory
clear all
% p1 : structure
p1=struct();
% E; modulus of elasticity
% A: area of cross section
% L: length of bar
% k: spring stiffness
E=70000;
A=200;
k=2000;
% generation of coordinates and connectivities
% numberElements: number of elements
p1.numberElements=3;
p1.numberNodes=4;
p1.elementNodes=[1 2; 2 3; 3 4];
p1.nodeCoordinates=[0 2000 4000 4000];
p1.xx=p1.nodeCoordinates;
% GDof: total degrees of freedom
p1.GDof=p1.numberNodes;
% for structure:
% displacements: displacement vector
% force : force vector
% stiffness: stiffness matrix
p1.displacements=zeros(p1.GDof,1);
p1.force=zeros(p1.GDof,1);
p1.stiffness=zeros(p1.GDof);
% applied load at node 2
p1.force(2)=8000.0;
% computation of the system stiffness matrix
for e=1:p1.numberElements;
% elementDof: element degrees of freedom (Dof)
elementDof=p1.elementNodes(e,:) ;
L=p1.nodeCoordinates(elementDof(2))-p1.nodeCoordinates(elementDof(1));
if e<3
ea(e)=E*A/L;
else
ea(e)=k;
end
p1.stiffness(elementDof,elementDof)=p1.stiffness(elementDof,elementDof)+ea(e)*[1 -1;-1 1];
end
% prescribed dofs
p1.prescribedDof=[1;4];
% solution
p1.displacements=solutionStructure(p1);
% output displacements/reactions
outputDisplacementsReactionsStructure(p1)
% Displacements
% ans =
% 1.0000 0
% 2.0000 3.3333
% 3.0000 0
% 4.0000 0
% reactions
% ans =
% 1.0000 -3.3333
% 3.0000 -3.3333
% 4.0000 -3.3333
outputDisplacementsReactionsStructure.m
function outputDisplacementsReactionsStructure(p)
% output of displacements and reactions in
% tabular form
% GDof: total number of degrees of freedom of
% the problem
% displacements
disp('Displacements')
jj=1:p.GDof;
[jj' p.displacements]
% reactions
F=p.stiffness*p.displacements;
reactions=F(p.prescribedDof);
disp('reactions')
[p.prescribedDof reactions]
shapeFunctionL2Structure.m
function shapeL2=shapeFunctionL2Structure(xi)
% shape function and derivatives for L2 elements
% shape : Shape functions
% naturalDerivatives: derivatives w.r.t. xi
% xi: natural coordinates (-1 ... +1)
shapeL2=struct()
shapeL2.shape=([1-xi,1+xi]/2)';
shapeL2.naturalDerivatives=[-1;1]/2;
end % end function shapeFunctionL2
solutionStructure.m
function displacements = solutionStructure(p)
% function to find solution in terms of global displacements
activeDof=setdiff([1:p.GDof]', [p.prescribedDof]);
U=p.stiffness(activeDof,activeDof)\p.force(activeDof);
displacements=zeros(p.GDof,1);
displacements(activeDof)=U;
end
第四章 2D桁架分析
笔记:单元刚度矩阵推导
例题1
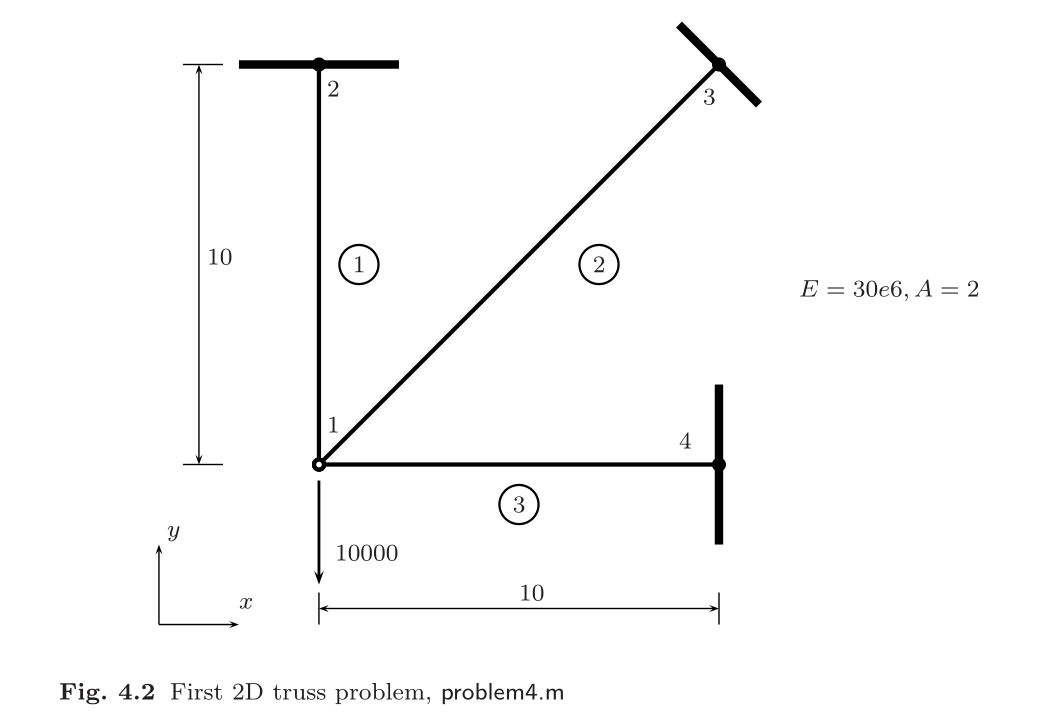
模型参数:
- 杨氏模量E=30e6 Pa ,泊松比 \(\mu\) =0.3
- A=2 m^2
- L=10 m
- P=10000 N
手算过程
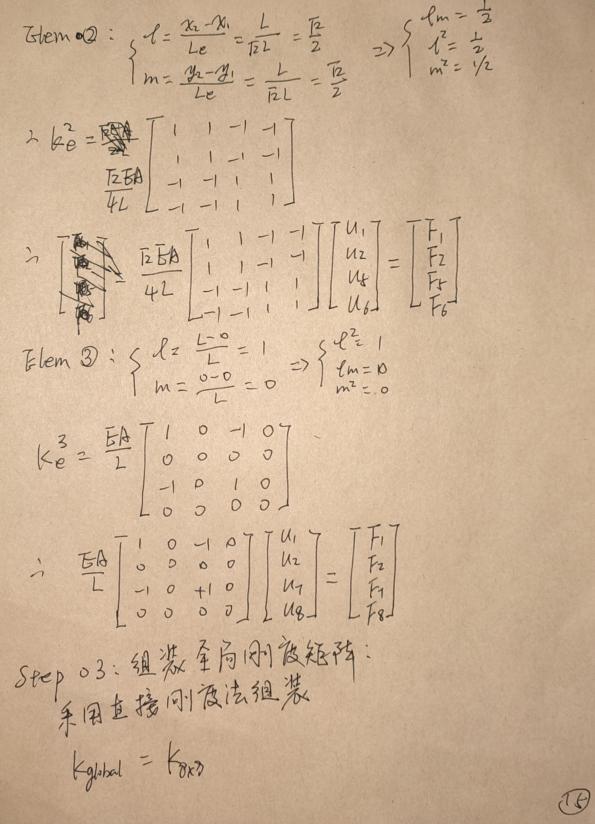
Abaqus 模拟结果
inp文件在码云repo中
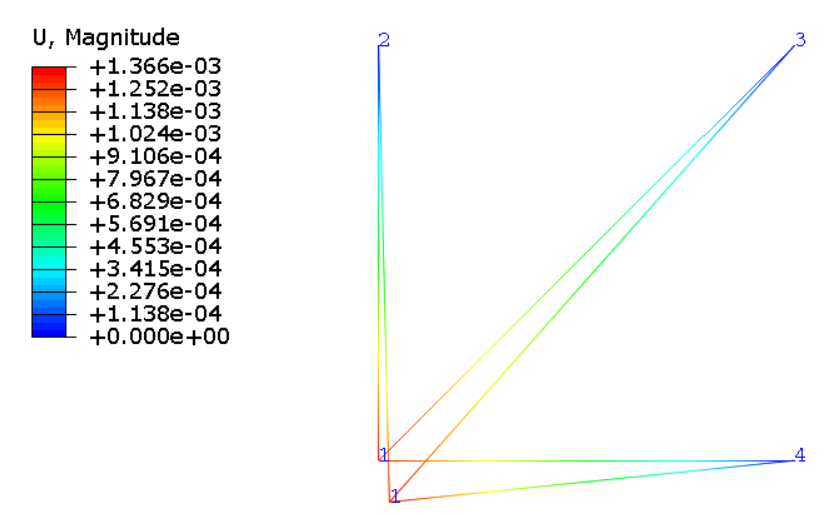
U and RF result :
********************************************************************************
Probe Values Report, written on Tue Apr 16 21:43:02 2024
Source
-------
ODB: C:/Users/Administrator/Documents/learnFEM/Matlb Fea Codes repo/fea-codes-of-matlab/chapter04/problem4/abaqus/Job-2.odb
Step: Step-1
Frame: Increment 1: Step Time = 1.000
Variable: U, U1
Probe values reported at nodes
Part Instance Node ID Orig. Coords Def. Coords
X Y Z X Y Z
-------------------------------------------------------------------------------------------------------------------------
PART-1-1 1 0. 0. 0. 345.178E-06 -1.32149E-03 0.
PART-1-1 2 0. 10. 0. 0. 10. 0.
PART-1-1 3 10. 10. 0. 10. 10. 0.
PART-1-1 4 10. 0. 0. 10. 0. 0.
Part Instance Node ID Attached elem U, U1 U, U2 RF, RF1 RF, RF2
--------------------------------------------------------------------------------------------------------------
PART-1-1 1 3 345.178E-06 -1.32149E-03 0. 0.
PART-1-1 2 1 0. -7.92893E-33 0. 7.92893E+03
PART-1-1 3 2 -2.07107E-33 -2.07107E-33 2.07107E+03 2.07107E+03
PART-1-1 4 3 2.07107E-33 0. -2.07107E+03 -0.
可以看出,手算和abaqus的U结果完全一致.
matlab 代码
problem4.m
% ! problem4.m --> based on <<MATLAB codes for Finite Element Analysis>>
clear ;
clc
format default
p=struct();
% define model parameters
p.E = 30e6;
p.A = 2;
p.L = 10;
p.P = -10000;
% define elems and nodes
p.nodes=[0 0 ; % node's coordinates (x,y)
0 p.L ;
p.L p.L ;
p.L 0 ];
p.elems=[1 2 ;
1 3 ;
1 4];
p.node_num=size(p.nodes,1);
p.elem_num=size(p.elems,1);
p.node_Coord_x=p.nodes(:,1);
p.node_Coord_y=p.nodes(:,2);
% define problem's dimension : 1D/2D/3D;
% = each node's dof
p.problem_dimension=size(p.nodes,2);
% global degree of freedom number
p.global_dof_num=2*p.node_num;
% define global Nodal displacement colum vector
p.displacements=zeros(p.global_dof_num,1);
p.node_forces=zeros(p.global_dof_num,1);
% define boundary conditions
% fixed dof
p.fix_dof=[3 4 5 6 7 8]';
% load dof and amplitude
p.load_dof=2;
% initial global stiffness matrix
p.global_stiffness_matrix=zeros(p.global_dof_num);
% compute all ElemStiffnessMatrix and assembly stiff matrix
elem_global_dof_num=2*size(p.elems,2);
p.elemStiffs=zeros(elem_global_dof_num,elem_global_dof_num,p.elem_num);
for i=1:p.elem_num
connectivity=p.elems(i,:);
% elem's all dof : a 2d truss node has 2 node,each node have 2 dof,
% i-th node --> U_(2*i-1) and U_(2*i) dof(displacement of node)
elem_dof=[connectivity(1)*2-1 connectivity(1)*2 ...
connectivity(2)*2-1 connectivity(2)*2];
node1_x=p.node_Coord_x(connectivity(1));
node1_y=p.node_Coord_y(connectivity(1));
node2_x=p.node_Coord_x(connectivity(2));
node2_y=p.node_Coord_y(connectivity(2));
elem_length=sqrt((node1_x-node2_x).^2+(node1_y-node2_y).^2);
l=(node2_x-node1_x)/elem_length;
m=(node2_y-node1_y)/elem_length;
k_e=(p.E*p.A/elem_length)*...
[l*l l*m -l*l -l*m;
l*m m*m -l*m -m*m;
-l*l -l*m l*l l*m;
-l*m -m*m l*m m*m];
p.elemStiffs(:,:,i)=k_e;
% assemble stiffness matrix
p.global_stiffness_matrix(elem_dof,elem_dof)=...
p.global_stiffness_matrix(elem_dof,elem_dof)+k_e;
end
% apply boundary condition
p.displacements(p.fix_dof)=0;
p.node_forces(p.load_dof)=p.P;
% solution KU=F
p = solutionStruct(p);
% show compute result
disp('displacements of dofs :')
disp([(1:p.global_dof_num)', p.displacements])
disp('forces of dofs :')
disp([(1:p.global_dof_num)',p.node_forces])
figure
axis equal
% plot undeformed mesh
draw_2Dtruss_mesh(p.nodes,p)
% plot deformed mesh
deformed_node_coordinate=cal_deformed_nodes(p,500.0);
draw_2Dtruss_mesh(deformed_node_coordinate,p)
title('位移变形')
grid on
function new_p=solutionStruct(p)
% free dof in structure
free_dof=setdiff((1:p.global_dof_num)',p.fix_dof);
% solute the equation :KU=F --> U=K\F
U=p.global_stiffness_matrix(free_dof,free_dof)\p.node_forces(free_dof);
p.displacements(free_dof)=U;
% displacements=zeros(p.global_dof_num,1);
p.node_forces=p.global_stiffness_matrix*p.displacements;
new_p=p;
end
function deformed_node_coordinate=cal_deformed_nodes(p,scale)
% initial
deformed_node_coordinate=p.nodes;
if p.problem_dimension==2
index1=1:2:p.global_dof_num;
index2=2:2:p.global_dof_num;
deformed_node_coordinate(:,1)=deformed_node_coordinate(:,1)+p.displacements(index1)*scale;
deformed_node_coordinate(:,2)=deformed_node_coordinate(:,2)+p.displacements(index2)*scale;
elseif p.problem_dimension==3
index1=1:3:p.global_dof_num;
index2=2:3:p.global_dof_num;
index3=3:3:p.global_dof_num;
deformed_node_coordinate(:,1)=deformed_node_coordinate(:,1)+p.displacements(index1);
deformed_node_coordinate(:,2)=deformed_node_coordinate(:,2)+p.displacements(index2);
deformed_node_coordinate(:,3)=deformed_node_coordinate(:,3)+p.displacements(index3);
end
end
function draw_2Dtruss_mesh(nodes,p)
xy=zeros(size(p.elems,2)*p.elem_num,p.problem_dimension);
cur1=1;
cur2=0;
for i =1:p.elem_num
connectivity=p.elems(i,:);
attach_node_num=size(connectivity,2);
cur1=cur2+1;
cur2=cur2+attach_node_num;
coord=zeros(attach_node_num,p.problem_dimension);
for j=1:size(connectivity,2)
coord(j,:)=nodes(connectivity(j),:);
end
xy(cur1:cur2,:)=coord;
end
line(xy(:,1),xy(:,2),"Marker","o","LineWidth",1,"Color",rand(1,3))
end
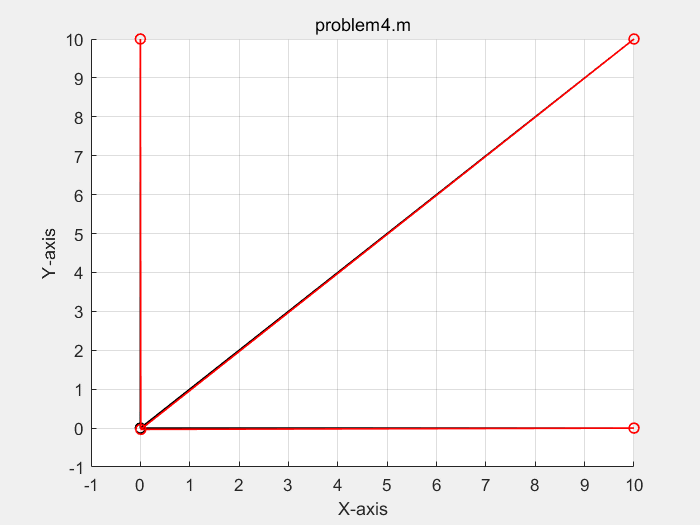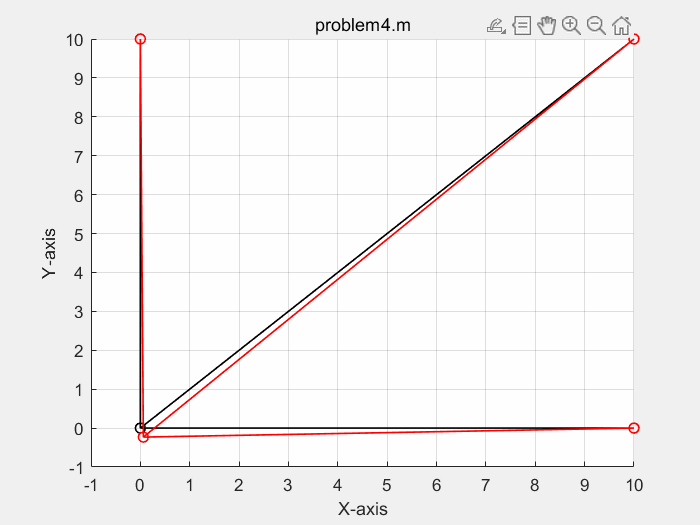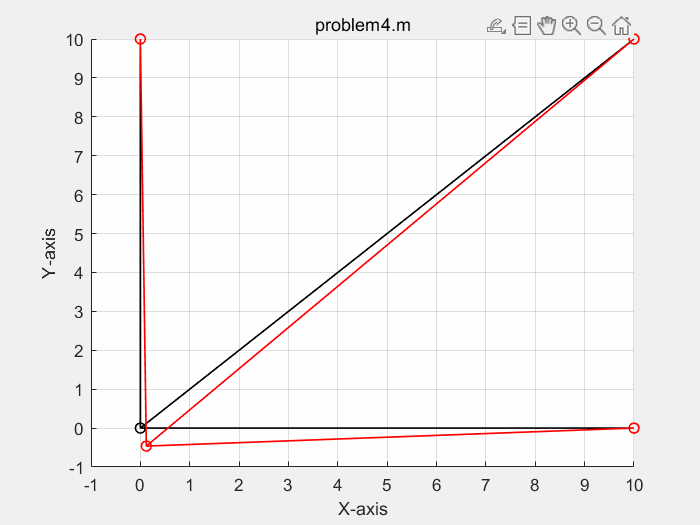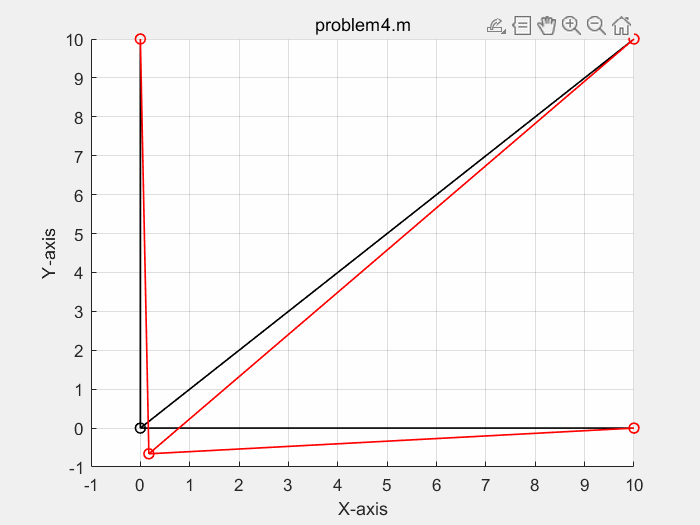
三种方式,计算结果一致
例题2
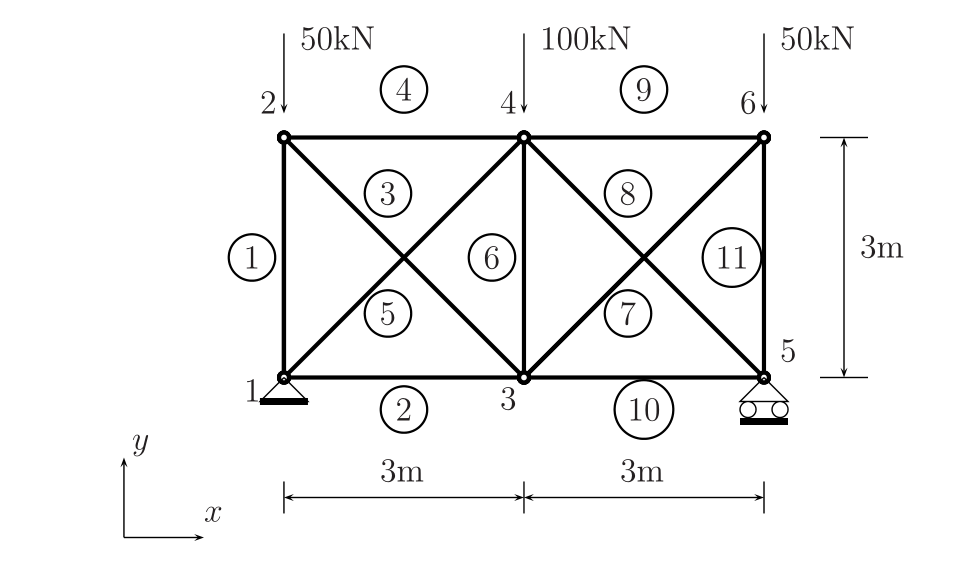
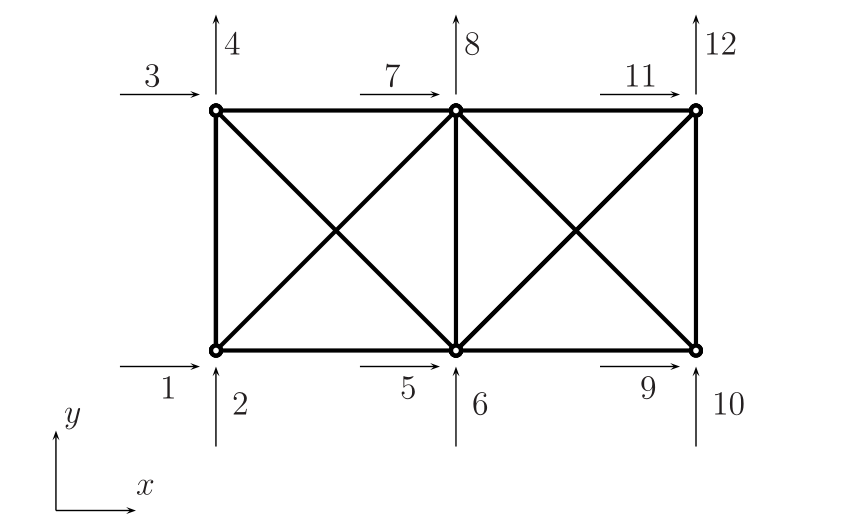
模型参数:
- 杨氏模量E = 70 GPa,泊松比 \(\mu\) = 0.3
- 桁架横截面积 A = \(3e^{-4} m^2\)
- L = 3 m
Abaqus 结果
待补充...
matlab 计算
基于problem4.m 代码,作如下修改即可:
% define model parameters
% unit:SI(m)
p.E = 70e9;
p.A = 3e-4;
p.L = 3;
p.P = 1000*[-50;-100;-50];
disp('单位制:SI(m)')
% define elems and nodes
p.nodes=[0 0 ; % node's coordinates (x,y)
0 p.L ;
p.L 0 ;
p.L p.L ;
2*p.L 0 ;
2*p.L p.L];
p.elems=[1 2 ;
1 3;
2 3;
2 4;
1 4;
3 4;
3 6;
4 5;
4 6;
3 5;
5 6];
......
% define boundary conditions
% fixed dof
p.fix_dof=[1 2 10]';
% load dof and amplitude
p.load_dof=[4 8 12]';
......
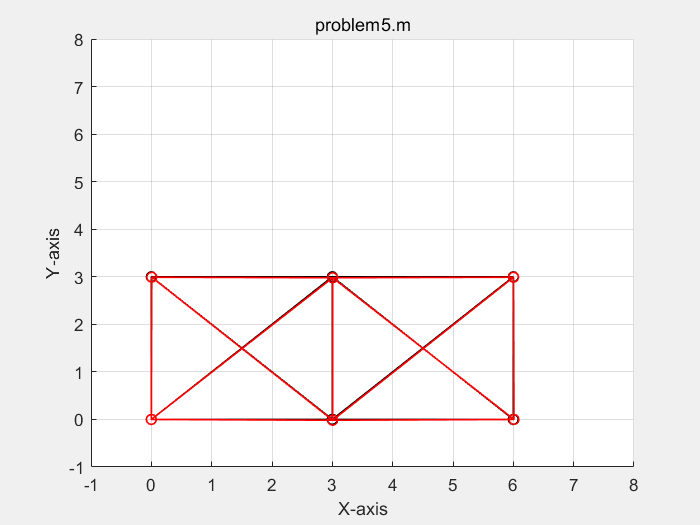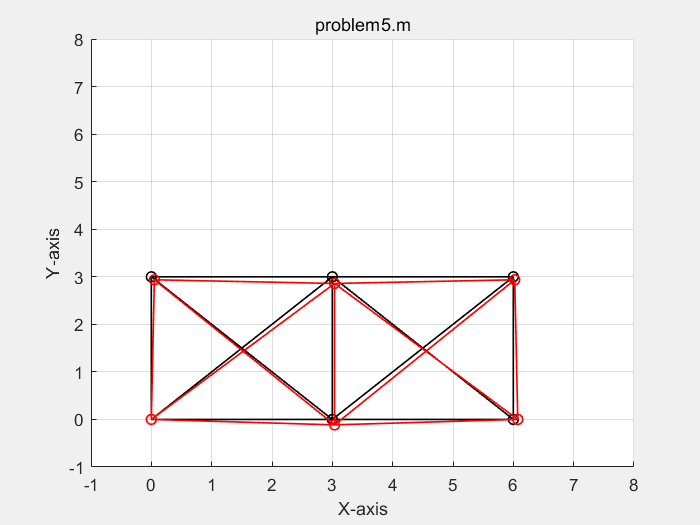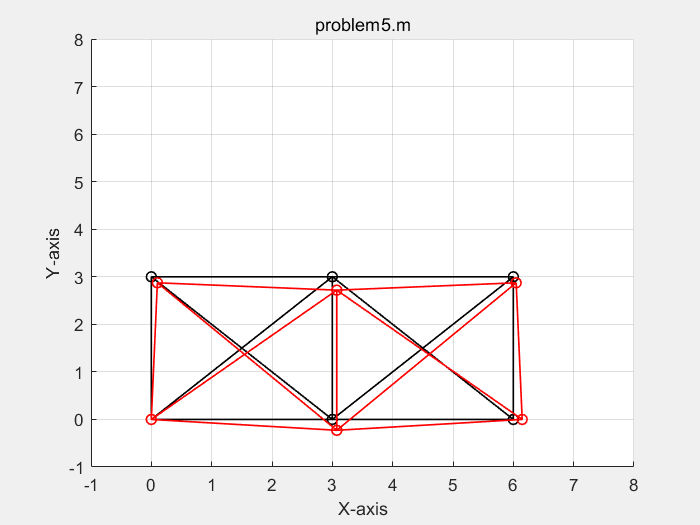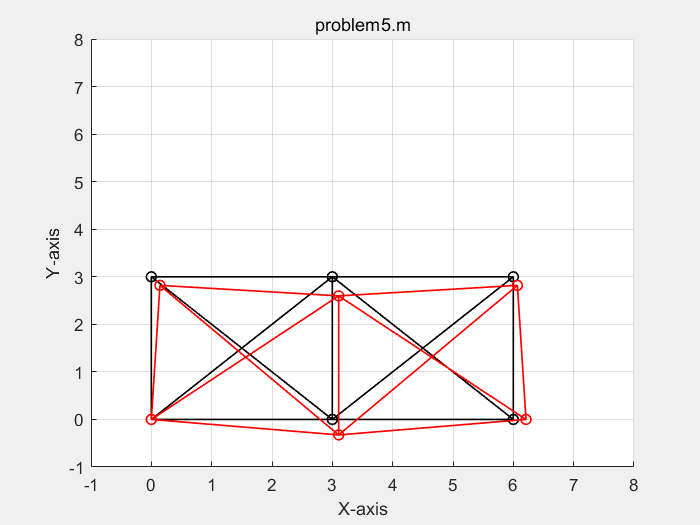
单位制:SI(m)
displacements of dofs :
1.0000 0
2.0000 0
3.0000 0.0071
4.0000 -0.0090
5.0000 0.0052
6.0000 -0.0163
7.0000 0.0052
8.0000 -0.0201
9.0000 0.0105
10.0000 0
11.0000 0.0034
12.0000 -0.0090
forces of dofs :
1.0e+05 *
0.0000 0.0000
0.0000 1.0000
0.0000 0.0000
0.0000 -0.5000
0.0001 -0.0000
0.0001 -0.0000
0.0001 -0.0000
0.0001 -1.0000
0.0001 0.0000
0.0001 1.0000
0.0001 0
0.0001 -0.5000
第五章 3D 桁架分析
笔记 - 3d truss 单元刚度矩阵
例题 1
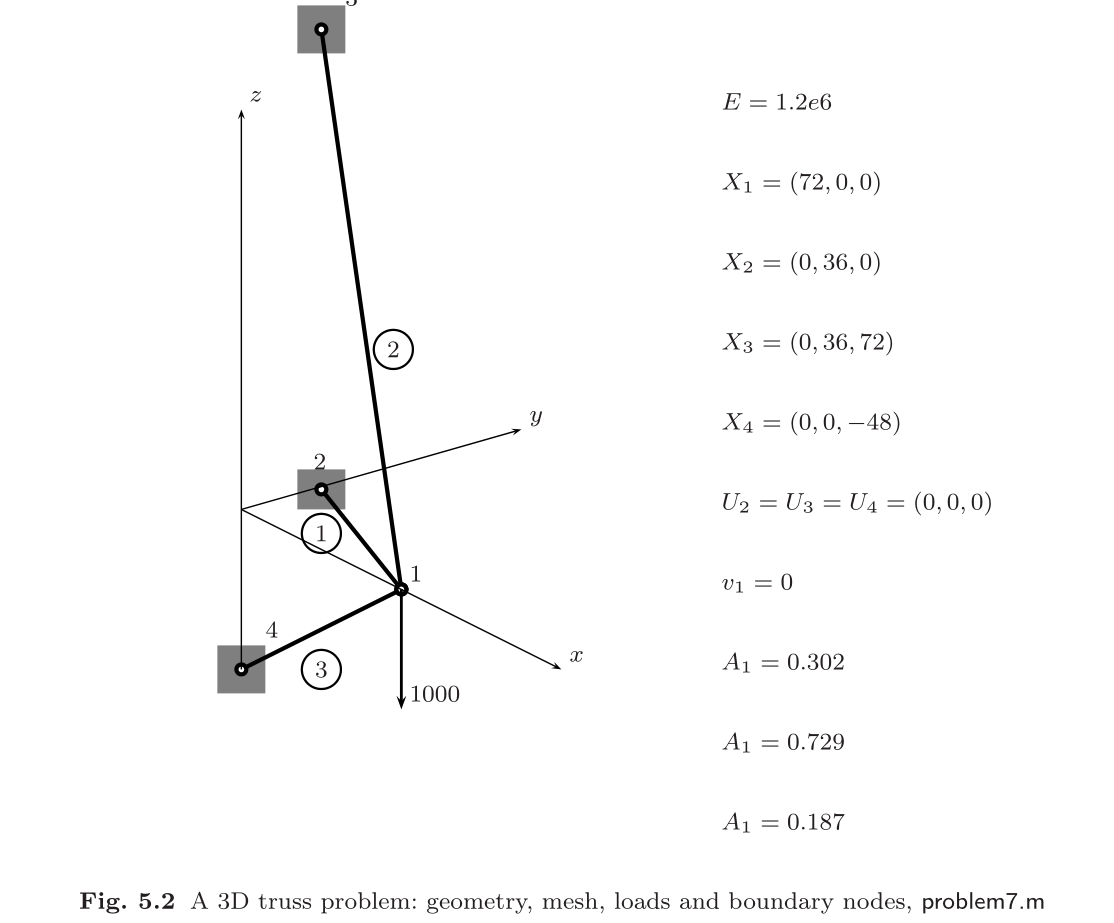
matlab 计算
- problem7.m 代码
% ! problem7.m --> based on <<MATLAB codes for Finite Element Analysis>>
clear ;
clc
format default
p=struct();
% define model parameters
% unit:SI(m)
p.E = 1.2e6;
p.A = [0.302 0.729 0.187]';
p.P = -1000;
disp('单位制:SI(m)')
% define elems and nodes
p.nodes=[72 0 0 ; % node's coordinates (x,y,z)
0 36 0;
0 36 72;
0 0 -48];
p.elems=[1 2 ;
1 3;
1 4];
p.node_num=size(p.nodes,1);
p.elem_num=size(p.elems,1);
p.node_Coord_x=p.nodes(:,1);
p.node_Coord_y=p.nodes(:,2);
p.node_Coord_z=p.nodes(:,3);
% define problem's dimension : 1D/2D/3D;
% = each node's dof
p.problem_dimension=size(p.nodes,2);
% global degree of freedom number
p.global_dof_num=p.problem_dimension*p.node_num;
% define global Nodal displacement colum vector
p.displacements=zeros(p.global_dof_num,1);
p.node_forces=zeros(p.global_dof_num,1);
% define boundary conditions
% fixed dof
p.fix_dof=[2 4 5 6 7 8 9 10 11 12]';
% load dof and amplitude
p.load_dof=3;
% initial global stiffness matrix
p.global_stiffness_matrix=zeros(p.global_dof_num);
% compute all ElemStiffnessMatrix and assembly stiff matrix
elem_global_dof_num=p.problem_dimension*size(p.elems,2);
p.elemStiffs=zeros(elem_global_dof_num,elem_global_dof_num,p.elem_num);
for i=1:p.elem_num
connectivity=p.elems(i,:);
% elem's all dof : a 3d truss node has 2 node,each node have 3 dof,
% i-th node --> U_(3*i-2) / U_(3*i-1) / U_(3*i) dof(displacement of node)
elem_dof=[connectivity(1)*3-2 connectivity(1)*3-1 connectivity(1)*3 ...
connectivity(2)*3-2 connectivity(2)*3-1 connectivity(2)*3];
node1_x=p.node_Coord_x(connectivity(1));
node1_y=p.node_Coord_y(connectivity(1));
node1_z=p.node_Coord_z(connectivity(1));
node2_x=p.node_Coord_x(connectivity(2));
node2_y=p.node_Coord_y(connectivity(2));
node2_z=p.node_Coord_z(connectivity(2));
elem_length=sqrt((node1_x-node2_x).^2+(node1_y-node2_y).^2+(node1_z-node2_z).^2);
Cx=(node2_x-node1_x)/elem_length;
Cy=(node2_y-node1_y)/elem_length;
Cz=(node2_z-node1_z)/elem_length;
T=[Cx*Cx Cx*Cy Cx*Cz;
Cx*Cy Cy*Cy Cy*Cz;
Cx*Cz Cy*Cz Cz*Cz];
k_e=(p.E*p.A(i)/elem_length)*[T -T;-T T];
p.elemStiffs(:,:,i)=k_e;
% assemble stiffness matrix
p.global_stiffness_matrix(elem_dof,elem_dof)=...
p.global_stiffness_matrix(elem_dof,elem_dof)+k_e;
end
% apply boundary condition
p.displacements(p.fix_dof)=0;
p.node_forces(p.load_dof)=p.P;
% solution KU=F
p = solutionStruct(p);
% calculate stress
p.stress=zeros(p.elem_num,1);
for i=1:p.elem_num
connectivity=p.elems(i,:);
% elem's all dof : a 3d truss node has 2 node,each node have 3 dof,
% i-th node --> U_(3*i-2) / U_(3*i-1) / U_(3*i) dof(displacement of node)
elem_dof=[connectivity(1)*3-2 connectivity(1)*3-1 connectivity(1)*3 ...
connectivity(2)*3-2 connectivity(2)*3-1 connectivity(2)*3];
node1_x=p.node_Coord_x(connectivity(1));
node1_y=p.node_Coord_y(connectivity(1));
node1_z=p.node_Coord_z(connectivity(1));
node2_x=p.node_Coord_x(connectivity(2));
node2_y=p.node_Coord_y(connectivity(2));
node2_z=p.node_Coord_z(connectivity(2));
elem_length=sqrt((node1_x-node2_x).^2+(node1_y-node2_y).^2+(node1_z-node2_z).^2);
Cx=(node2_x-node1_x)/elem_length;
Cy=(node2_y-node1_y)/elem_length;
Cz=(node2_z-node1_z)/elem_length;
p.stress(i)=(p.E/elem_length)*[-Cx -Cy -Cz Cx Cy Cz]*p.displacements(elem_dof);
end
% show compute result
disp('displacements of dofs :')
disp([(1:p.global_dof_num)', p.displacements])
disp('forces of dofs :')
disp([(1:p.global_dof_num)',p.node_forces])
disp('3d truss elem stress :')
disp([(1:p.elem_num)',p.stress])
figure
axis equal
% plot undeformed mesh
draw_3Dtruss_mesh(p.nodes,p)
% plot deformed mesh
deformed_node_coordinate=cal_deformed_nodes(p,50.0);
draw_3Dtruss_mesh(deformed_node_coordinate,p)
title('位移变形')
grid on
function draw_3Dtruss_mesh(nodes,p)
xy=zeros(size(p.elems,2)*p.elem_num,p.problem_dimension);
cur1=1;
cur2=0;
for i =1:p.elem_num
connectivity=p.elems(i,:);
attach_node_num=size(connectivity,2);
cur1=cur2+1;
cur2=cur2+attach_node_num;
coord=zeros(attach_node_num,p.problem_dimension);
for j=1:size(connectivity,2)
coord(j,:)=nodes(connectivity(j),:);
end
xy(cur1:cur2,:)=coord;
end
line(xy(:,1),xy(:,2),xy(:,3),"Marker","o","LineWidth",1,"Color",rand(1,3))
end
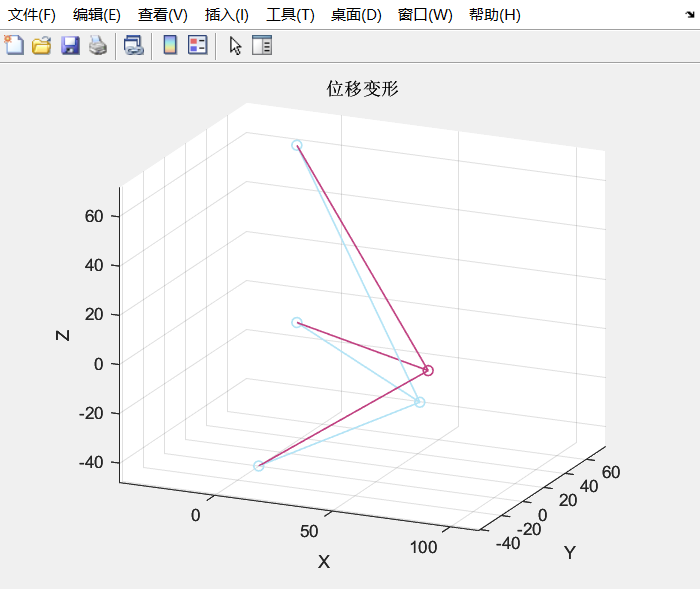
- 计算结果
单位制:SI(m)
displacements of dofs :
1.0000 -0.0711
2.0000 0
3.0000 -0.2662
4.0000 0
5.0000 0
6.0000 0
7.0000 0
8.0000 0
9.0000 0
10.0000 0
11.0000 0
12.0000 0
forces of dofs :
1.0e+03 *
0.0010 0
0.0020 -0.2232
0.0030 -1.0000
0.0040 0.2561
0.0050 -0.1281
0.0060 0
0.0070 -0.7024
0.0080 0.3512
0.0090 0.7024
0.0100 0.4463
0.0110 0
0.0120 0.2976
3d truss elem stress :
1.0e+03 *
0.0010 -0.9482
0.0020 1.4454
0.0030 -2.8685
例题2
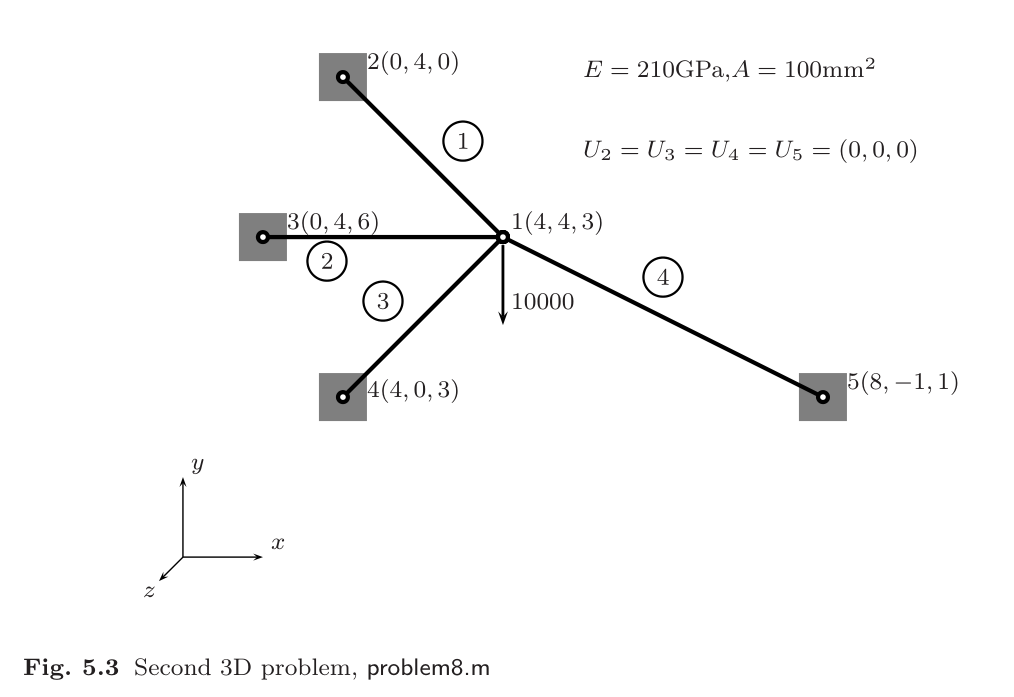
模型参数:
- E = 210000 Mpa,\(\mu\)=0.3
- A = 100 mm^2
- P =-10000 N
Abaqus 结果
waiting...
Matlab 计算
- problem8.m
基于problem7.m,修改参数,即可.
% define model parameters
% unit:SI(mm)
p.E = 210000;
p.A = 100;
p.P = -10000;
disp('单位制:SI(mm)')
% define elems and nodes
p.nodes=[4 4 3 ; % node's coordinates (x,y,z)
0 4 0;
0 4 6;
4 0 3;
8 -1 1];
p.elems=[1 2 ;
1 3;
1 4;
1 5];
......
% define boundary conditions
% fixed dof
p.fix_dof=[4:15]';
% load dof and amplitude
p.load_dof=2;
......
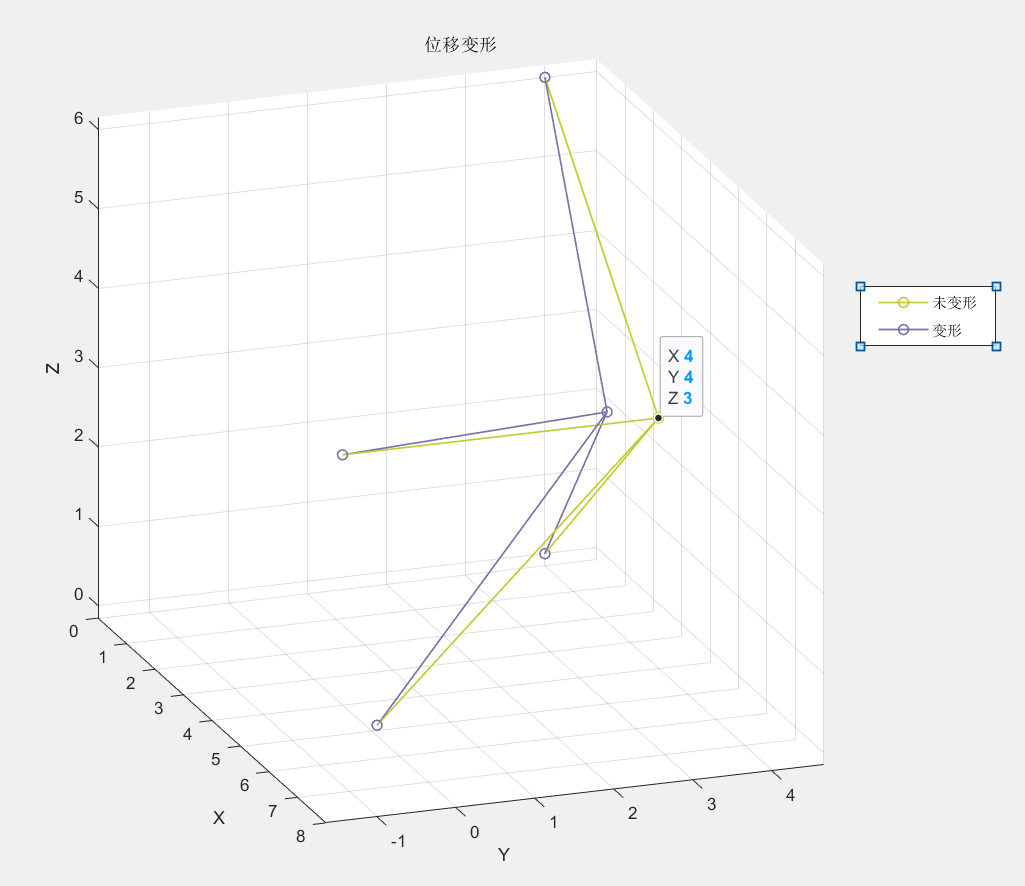
- 计算结果
单位制:SI(mm)
displacements of dofs :
1.0000 -0.0003
2.0000 -0.0015
3.0000 0.0003
forces of dofs :
1.0e+04 *
0.0004 0.0271
0.0005 0
0.0006 0.0203
0.0007 0.1355
0.0008 0
0.0009 -0.1016
0.0010 0
0.0011 0.7968
0.0012 0
0.0013 -0.1626
0.0014 0.2032
0.0015 0.0813
3d truss elem stress :
1.0000 -3.3865
2.0000 -16.9326
3.0000 -79.6809
4.0000 -27.2610
deformed nodes:
3.8791 3.3929 3.1075
0 4.0000 0
0 4.0000 6.0000
4.0000 0 3.0000
8.0000 -1.0000 1.0000
第六章 2D 欧拉-伯努利梁分析
单元刚度矩阵推导
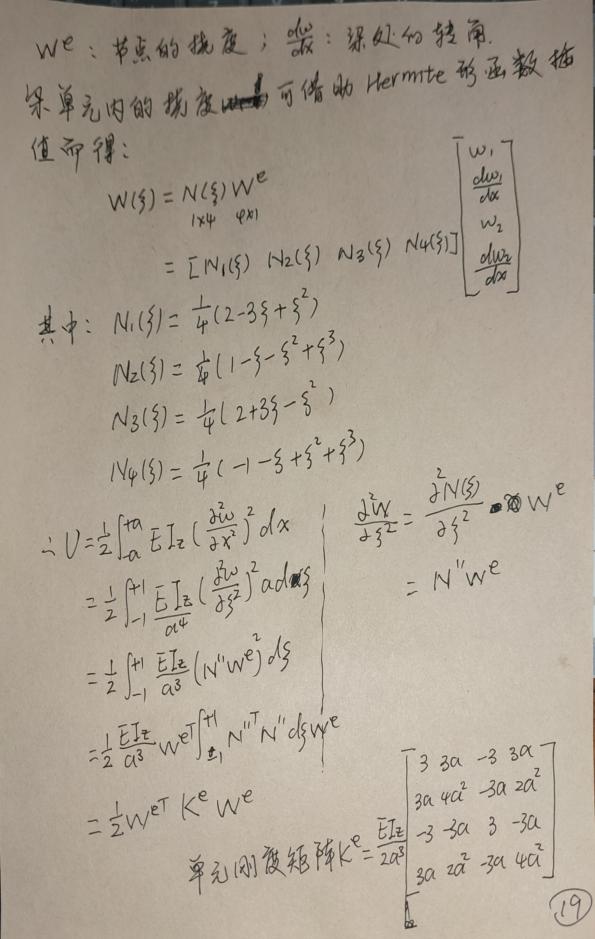
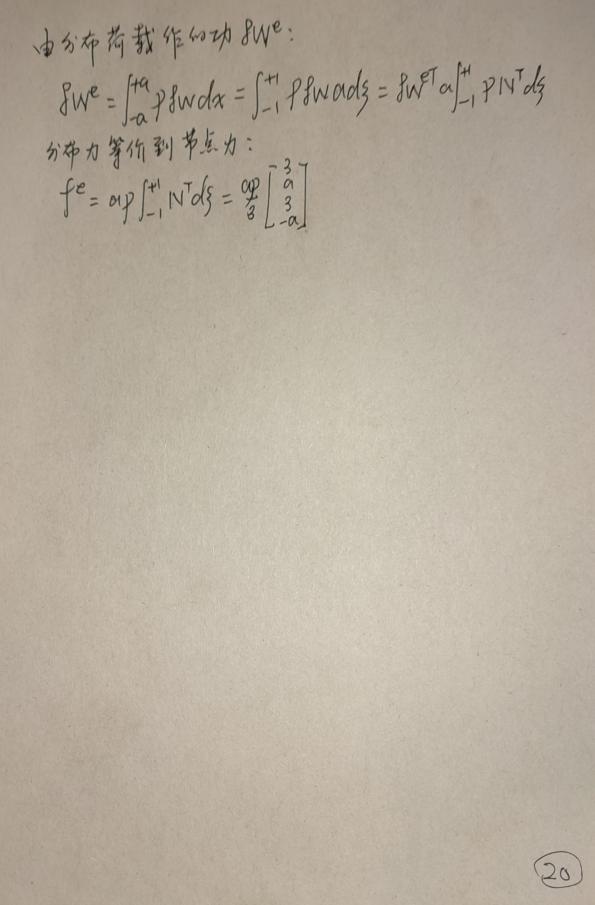
例题 1
consider a simply-supported and clamped Bernoulli beam in bending, under uniform load
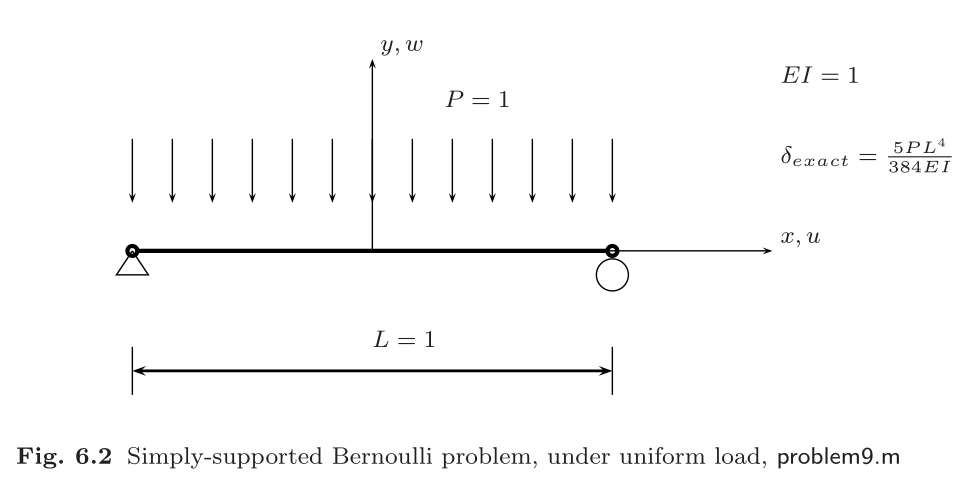
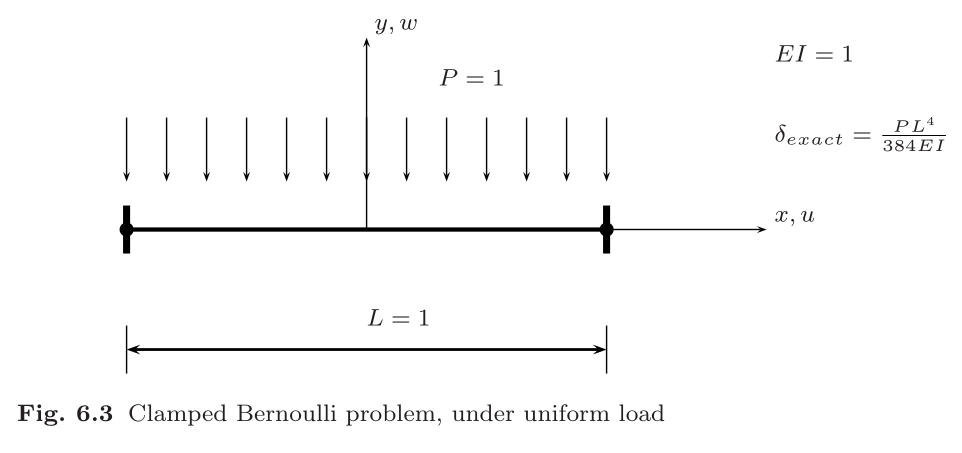
Abaqus 计算
Matlab 计算
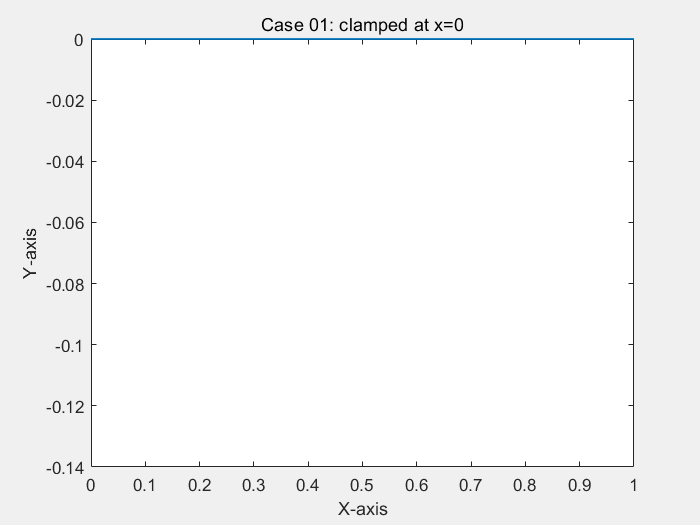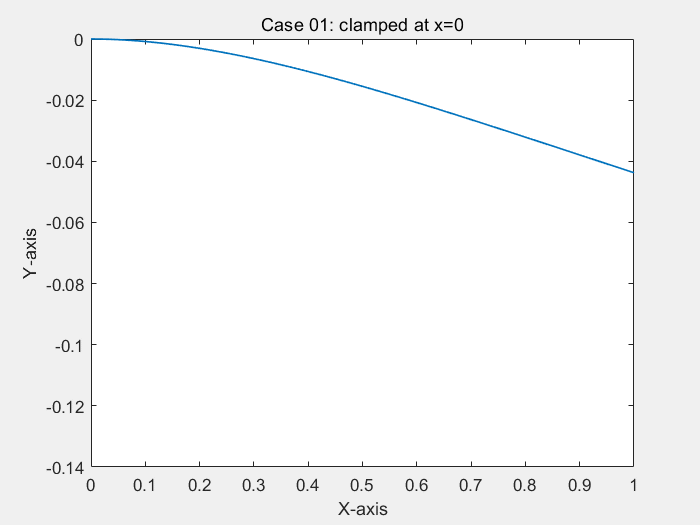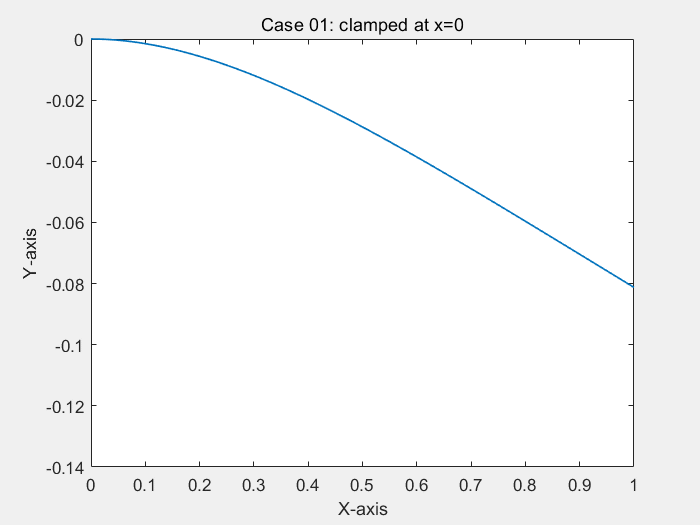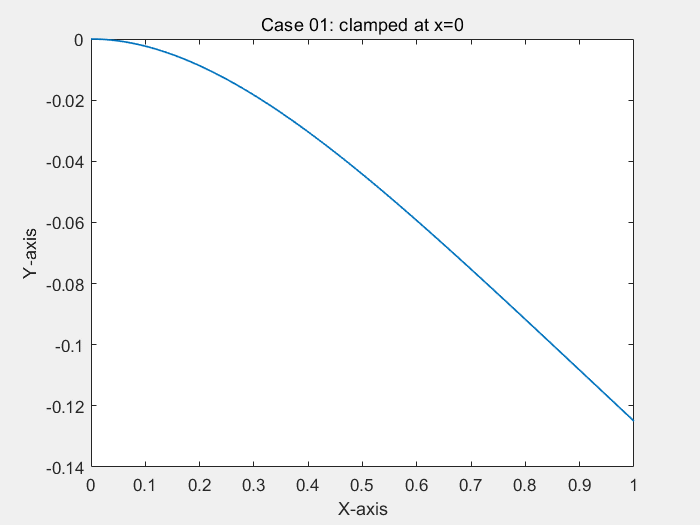
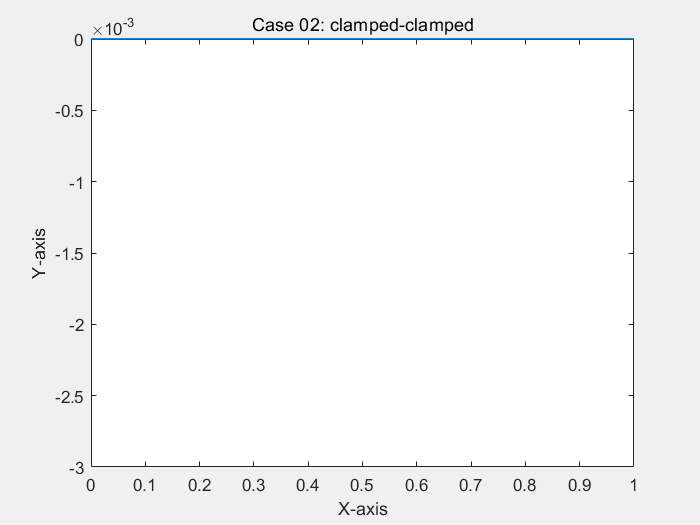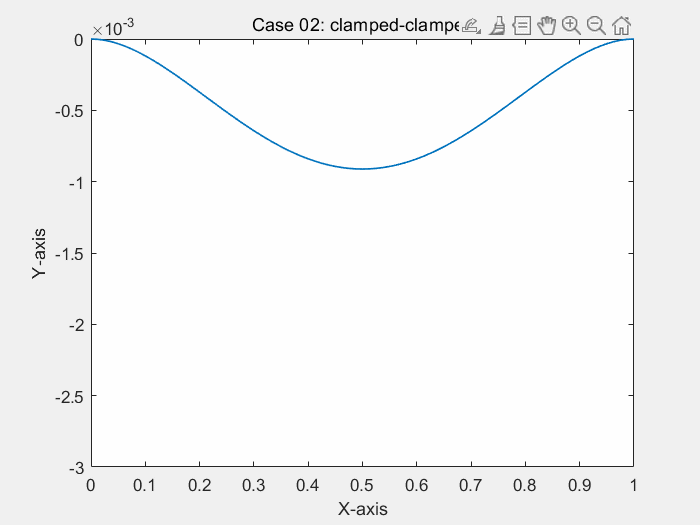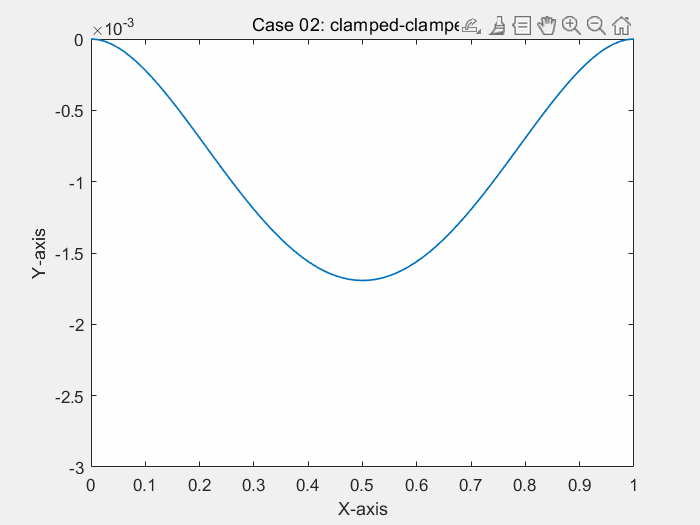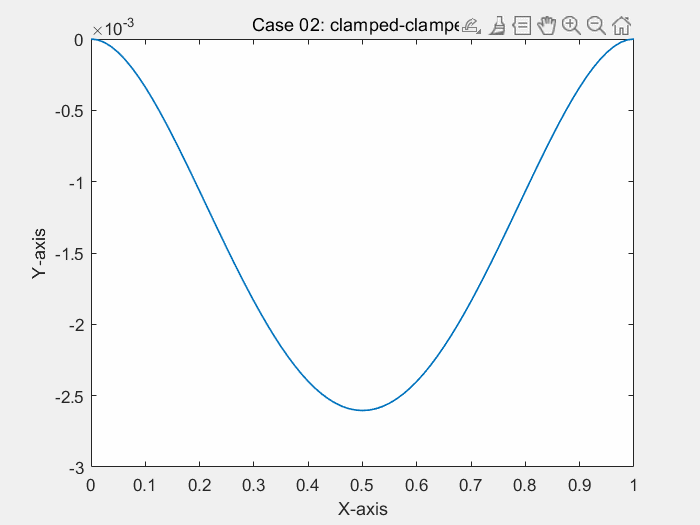
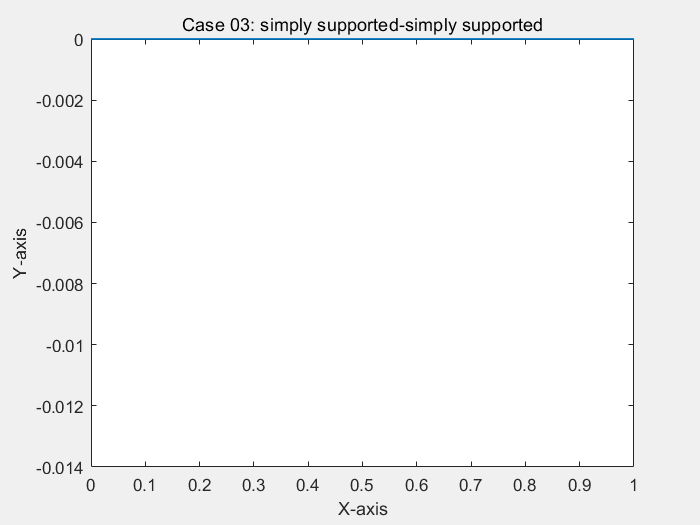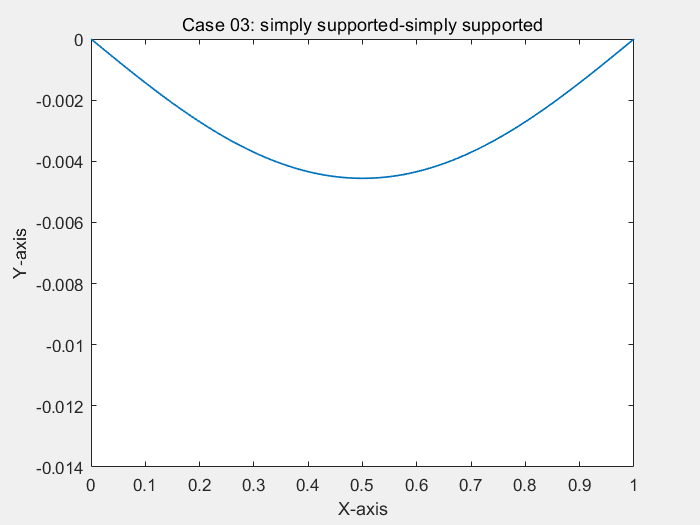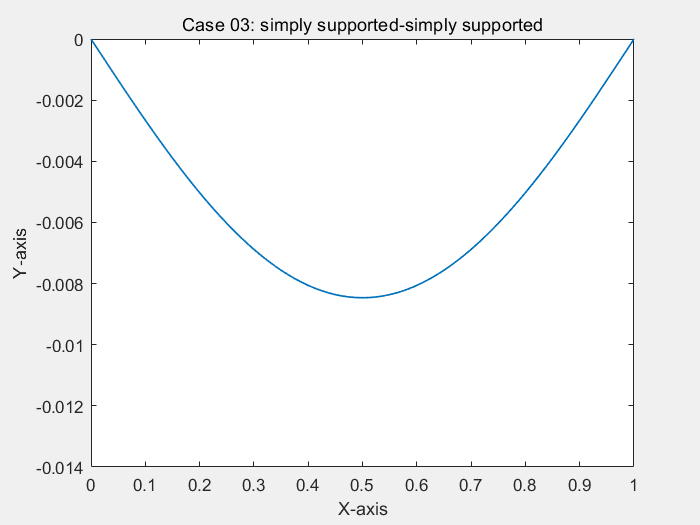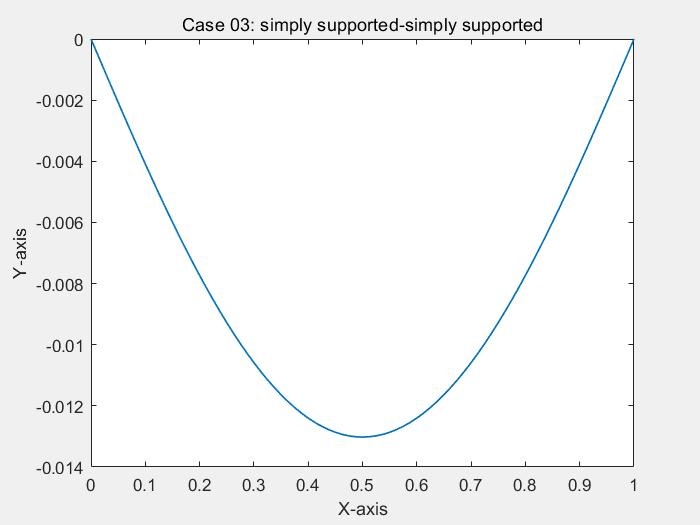
% ! problem9.m --> based on <<MATLAB codes for Finite Element Analysis>>
clear ;
clc
format default
p=struct();
Case=1;
% define model parameters
% unit:SI(mm)
p.EI = 1;
p.L = 1;
% * distribute force
p.P = -1;
% define elems num of bornoulli beam
p.elem_num=80;
% define problem's dimension : 1D/2D/3D;
% = each node's dof
p.problem_dimension=2;
% ? -------------------------------
% node's coordinates (x)
p.nodes=linspace(0,p.L,p.elem_num+1)';
p.elems=zeros(p.elem_num,2);
for i=1:p.elem_num
p.elems(i,1)=i;
p.elems(i,2)=i+1;
end
p.node_num=size(p.nodes,1);
p.node_Coord_x=p.nodes(:,1);
% global degree of freedom number
p.global_dof_num=2*p.node_num;
% define global Nodal displacement colum vector
p.displacements=zeros(p.global_dof_num,1);
p.node_forces=zeros(p.global_dof_num,1);
% define boundary conditions
if Case==1
% Case 01: clamped at x=0
% fixed dof
p.fix_dof=[1 2]';
end
if Case==2
% Case 02: clamped-clamped
% fixed dof
p.fix_dof=[1 p.elem_num*2+1 2 p.elem_num*2+2]';
end
if Case==3
% Case 03: simply supported-simply supported
p.fix_dof=[1 2*p.elem_num+1]';
end
% initial global stiffness matrix
p.global_stiffness_matrix=zeros(p.global_dof_num);
% compute all ElemStiffnessMatrix and assembly stiff matrix
elem_global_dof_num=p.problem_dimension*size(p.elems,2);
p.elemStiffs=zeros(elem_global_dof_num,elem_global_dof_num,p.elem_num);
for i=1:p.elem_num
connectivity=p.elems(i,:);
% elem's all dof : a 3d truss node has 2 node,each node have 2 dof,
% i-th node --> w_(2*i-1) / dw_(2*i-2) / dof(displacement of node)
elem_dof=[connectivity(1)*2-1 connectivity(1)*2 ...
connectivity(2)*2-1 connectivity(2)*2 ];
node1_x=p.node_Coord_x(connectivity(1));
node2_x=p.node_Coord_x(connectivity(2));
elem_length=node2_x-node1_x;
a=0.5*elem_length;
k_e=(p.EI/(a^3))*0.5*[3 3*a -3 3*a;
3*a 4*a*a -3*a 2*a*a;
-3 -3*a 3 -3*a;
3*a 2*a*a -3*a 4*a*a];
p.elemStiffs(:,:,i)=k_e;
p.node_forces(elem_dof)=p.node_forces(elem_dof)+((p.P*a/3)*[3 a 3 -a])';
% assemble stiffness matrix
p.global_stiffness_matrix(elem_dof,elem_dof)=...
p.global_stiffness_matrix(elem_dof,elem_dof)+k_e;
end
% apply boundary condition
p.displacements(p.fix_dof)=0;
% solution KU=F
p = solutionStruct_bornoulli_beam(p);
plot(p.node_Coord_x,p.displacements(1:2:2*p.node_num),'.')
minDispalce=min(p.displacements(1:2:2*p.node_num));
text(0.35,0.5*minDispalce,"挠度最小值:"+minDispalce)
if Case==1
title("Case 01: clamped at x=0")
end
if Case==2
title("Case 02: clamped-clamped")
end
if Case==3
title("Case 03: simply supported-simply supported")
end
function new_p=solutionStruct_bornoulli_beam(p)
% free dof in structure
free_dof=setdiff((1:p.global_dof_num)',p.fix_dof);
% solute the equation :KU=F --> U=K\F
U=p.global_stiffness_matrix(free_dof,free_dof)\p.node_forces(free_dof);
p.displacements(free_dof)=U;
% displacements=zeros(p.global_dof_num,1);
p.node_forces_fu=p.global_stiffness_matrix*p.displacements;
new_p=p;
end
例题2
matlab 计算
- problem10.m
% ! problem10.m --> based on <<MATLAB codes for Finite Element Analysis>>
clear;
clc;
format compact;
p=struct();
% define model paraeters
p.E=1000000;
p.L=10;
t=p.L/1000;
p.Iz=(1*t^3)/12;
p.P=-1000;
% define elems of bornoulli beam
p.elem_num=20;
% dof of each nornoulli beam nodes
p.bornoulli_node_dof_num=2;
p.spring_k=100;
% -------------------------------
% node's coordinate
p.nodes=linspace(0,p.L,p.elem_num+1)';
p.elems=zeros(p.elem_num,2);
for i=1:p.elem_num
p.elems(i,1)=i;
p.elems(i,2)=i+1;
end
p.node_num=size(p.nodes,1);
p.node_Coord_x=p.nodes(:,1);
% global degree of freedom number:
% ! bornoulli_beam node's dof + 1 spring node's dof
p.global_dof_num=2*p.node_num;
% define global Nodal displacement colum vector
p.displacements=zeros(p.global_dof_num+1,1);
p.node_forces=zeros(p.global_dof_num+1,1);
% define boundary conditions
% ! BC: clamped at x=0
p.fix_dof=[1,2,p.global_dof_num+1]';
% initial global stiffness matrix
p.global_stiffness_matrix=zeros(p.global_dof_num+1);
% compute all ElemStiffnessMatrix and assembly stiff matrix
beam_dof_num=p.bornoulli_node_dof_num*size(p.elems,2);
p.elemStiffs=zeros(beam_dof_num,beam_dof_num,p.elem_num);
for i=1:p.elem_num
connectivity=p.elems(i,:);
% elem's all dof : a 3d truss node has 2 node,each node have 2 dof,
% i-th node --> w_(2*i-1) / dw_(2*i-2) / dof(displacement of node)
elem_dof=[connectivity(1)*2-1 connectivity(1)*2 ...
connectivity(2)*2-1 connectivity(2)*2 ];
node1_x=p.node_Coord_x(connectivity(1));
node2_x=p.node_Coord_x(connectivity(2));
elem_length=node2_x-node1_x;
a=0.5*elem_length;
k_e=(p.E*p.Iz/(a^3))*0.5*[3 3*a -3 3*a;
3*a 4*a*a -3*a 2*a*a;
-3 -3*a 3 -3*a;
3*a 2*a*a -3*a 4*a*a];
p.elemStiffs(:,:,i)=k_e;
p.node_forces(elem_dof)=p.node_forces(elem_dof)+((p.P*a/3)*[3 a 3 -a])';
% assemble stiffness matrix
p.global_stiffness_matrix(elem_dof,elem_dof)=...
p.global_stiffness_matrix(elem_dof,elem_dof)+k_e;
end
% add spring nodes into global_stiffness_matrix
p.global_stiffness_matrix([p.global_dof_num-1,p.global_dof_num+1],[p.global_dof_num-1,p.global_dof_num+1])=...
p.global_stiffness_matrix([p.global_dof_num-1,p.global_dof_num+1],[p.global_dof_num-1,p.global_dof_num+1])+p.spring_k*[1,-1;-1,1];
% apply boundary condition
p.node_forces(p.fix_dof)=0;
% solution KU=F
p=solutionStruct(p);
% ! display result
disp('Bornoulli beam result !')
disp('beam挠度:')
omega_index=(1:2:p.global_dof_num)';
disp([omega_index,p.displacements(omega_index)])
disp('beam转角:')
theta_index=(2:2:p.global_dof_num)';
disp([theta_index,p.displacements(theta_index)])
disp('beam支反力:')
disp([p.fix_dof,p.node_forces(p.fix_dof)])
plot(p.node_Coord_x,p.displacements(omega_index),'-')
title('Problem10.m')
- 计算结果
Bornoulli beam result !
beam挠度:
1.0e+05 *
0.0000 0
0.0000 -0.1722
0.0001 -0.6300
0.0001 -1.2909
0.0001 -2.0800
0.0001 -2.9297
0.0001 -3.7800
0.0001 -4.5785
0.0002 -5.2801
0.0002 -5.8473
0.0002 -6.2501
0.0002 -6.4661
0.0003 -6.4802
0.0003 -6.2849
0.0003 -5.8802
0.0003 -5.2737
0.0003 -4.4803
0.0003 -3.5225
0.0004 -2.4303
0.0004 -1.2413
0.0004 -0.0004
beam转角:
1.0e+05 *
0.0000 0
0.0000 -0.6588
0.0001 -1.1450
0.0001 -1.4738
0.0001 -1.6600
0.0001 -1.7188
0.0001 -1.6650
0.0002 -1.5138
0.0002 -1.2800
0.0002 -0.9788
0.0002 -0.6250
0.0002 -0.2338
0.0003 0.1800
0.0003 0.6012
0.0003 1.0149
0.0003 1.4062
0.0003 1.7599
0.0004 2.0612
0.0004 2.2949
0.0004 2.4462
0.0004 2.4999
beam支反力:
1.0e+04 *
0.0001 0.6000
0.0002 1.2479
0.0043 0.3750
第7章 2d Frame单元静态分析
单元刚度矩阵推导
参见博文:【刚度矩阵推导】2d frame 单元
例题
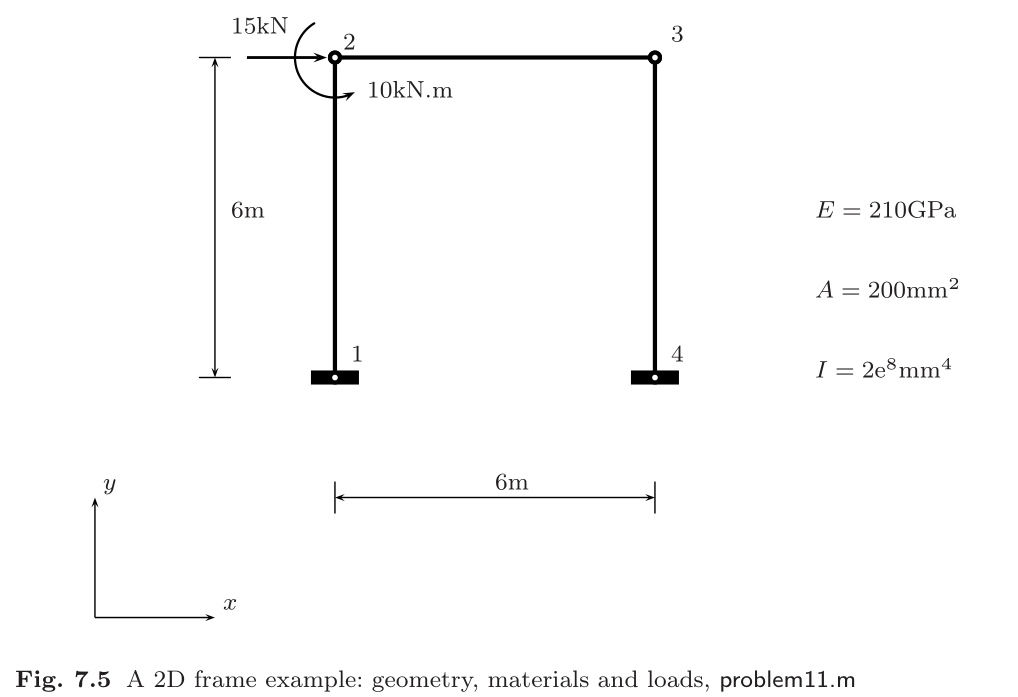
Matlab 代码
% ! problem10.m --> based on <<MATLAB codes for Finite Element Analysis>>
% ! chpater 7 using 2d-frame element
clear ;
clc
format default
p=struct();
% define model parameters
p.E = 210000; % SI(mm)
p.A = 200;
p.P = [15000 10e6]';
p.Iz=2e8;
% define elems and nodes
p.nodes=[0 0 ; % node's coordinates (x,y)
0 6000 ;
6000 6000 ;
6000 0;];
p.elems=[1 2; 2 3; 3 4;];
p.node_num=size(p.nodes,1);
p.elem_num=size(p.elems,1);
p.node_Coord_x=p.nodes(:,1);
p.node_Coord_y=p.nodes(:,2);
% define problem's dimension = each node's dof
p.problem_dimension=3;
% global degree of freedom number
p.global_dof_num=3*p.node_num;
% define global Nodal displacement colum vector
p.displacements=zeros(p.global_dof_num,1);
p.node_forces=zeros(p.global_dof_num,1);
% define boundary conditions
% fixed dof
p.fix_dof=[1 2 3 10 11 12]';
% load dof and amplitude
p.load_dof=[4 6]';
% initial global stiffness matrix
p.global_stiffness_matrix=zeros(p.global_dof_num);
% compute all ElemStiffnessMatrix and assembly stiff matrix
elem_global_dof_num=p.problem_dimension*size(p.elems,2);
p.elemStiffs=zeros(elem_global_dof_num,elem_global_dof_num,p.elem_num);
for i=1:p.elem_num
connectivity=p.elems(i,:);
% elem's all dof : a 2d frame elem has 2 node,each node have 3 dof,
% i-th node --> U_(3*i-2) and U_(3*i-1) and U_(3*i) dof(displacement of node)
elem_dof=[connectivity(1)*3-2 connectivity(1)*3-1 connectivity(1)*3 connectivity(2)*3-2 connectivity(2)*3-1 connectivity(2)*3];
node1_x=p.node_Coord_x(connectivity(1));
node1_y=p.node_Coord_y(connectivity(1));
node2_x=p.node_Coord_x(connectivity(2));
node2_y=p.node_Coord_y(connectivity(2));
elem_length=sqrt((node1_x-node2_x).^2+(node1_y-node2_y).^2);
l=(node2_x-node1_x)/elem_length;
m=(node2_y-node1_y)/elem_length;
% coordinate transform matrix: U_l=L*U_g
L=[l m 0 0 0 0;
-m l 0 0 0 0;
0 0 1 0 0 0;
0 0 0 l m 0;
0 0 0 -m l 0;
0 0 0 0 0 1;];
% in local coordinates, the stiffness matrix of the frame element is obtained by com-
% bination of the stiffness of the bar element and the Bernoulli beam element
E=p.E;
A=p.A;
Iz=p.Iz;
k_e_local=zeros(elem_global_dof_num,elem_global_dof_num);
k_e_local(1,1)=(E*A)/elem_length;
k_e_local(4,4)=(E*A)/elem_length;
k_e_local(1,4)=-(E*A)/elem_length;
k_e_local(4,1)=-(E*A)/elem_length;
k_e_local(2,2)=12*E*Iz/(elem_length^3);
k_e_local(2,3)=6*E*Iz/(elem_length^2);
k_e_local(2,5)=12*E*Iz/(elem_length^3);
k_e_local(2,6)=6*E*Iz/(elem_length^2);
k_e_local(3,2)=6*E*Iz/(elem_length^2);
k_e_local(5,2)=12*E*Iz/(elem_length^3);
k_e_local(6,2)=6*E*Iz/(elem_length^2);
k_e_local(3,3)=4*E*Iz/(elem_length);
k_e_local(3,5)=-6*E*Iz/(elem_length*elem_length);
k_e_local(3,6)=2*E*Iz/elem_length;
k_e_local(6,3)=2*E*Iz/elem_length;
k_e_local(5,3)=-6*E*Iz/(elem_length*elem_length);
k_e_local(5,5)=12*E*Iz/(elem_length*elem_length*elem_length);
k_e_local(5,6)=-6*E*Iz/(elem_length*elem_length);
k_e_local(6,5)=-6*E*Iz/(elem_length*elem_length);
k_e_local(6,6)=4*E*Iz/elem_length;
k_e_global=L' *k_e_local *L;
p.elemStiffs(:,:,i)=k_e_global;
% assemble stiffness matrix
p.global_stiffness_matrix(elem_dof,elem_dof)=...
p.global_stiffness_matrix(elem_dof,elem_dof)+k_e_global;
end
% apply boundary condition
p.displacements(p.fix_dof)=0;
p.node_forces(p.load_dof)=p.P;
% solution KU=F
p = solutionStruct(p);
% show compute result
disp('displacements of dofs :')
disp([(1:p.global_dof_num)', p.displacements])
disp('forces of dofs :')
disp([(1:p.global_dof_num)',p.node_forces])
figure
axis equal
% plot undeformed mesh
draw_2Dtruss_mesh(p.nodes,p,'black')
deform_scale=500;
deformed_node_coordinate=[p.node_Coord_x+deform_scale*p.displacements(3*(1:p.node_num)-2), ...
p.node_Coord_y+deform_scale*p.displacements(3*(1:p.node_num)-1)];
% plot deformed mesh
draw_2Dtruss_mesh(deformed_node_coordinate,p,'red')
title('位移变形')
grid on
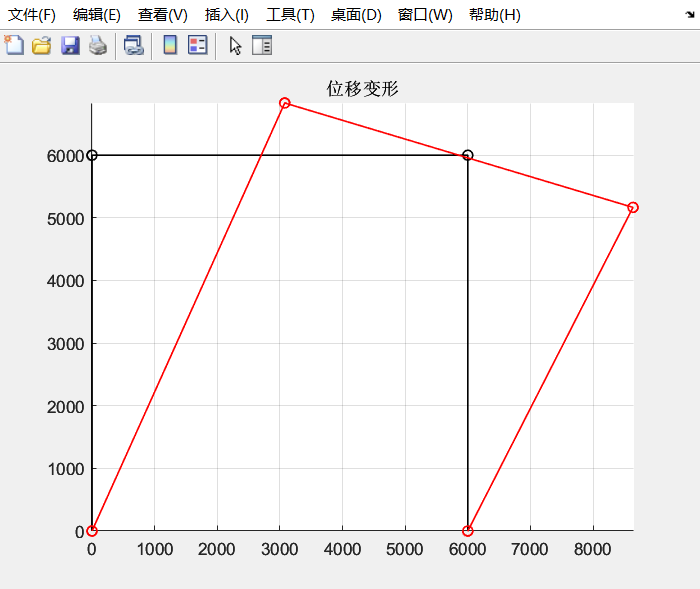
第八章 3d Frame单元静态分析
略
第九章 analysis of grids
略
第十章 Timoshenko beams 静态分析
与欧拉-伯努利梁公式不同,Timoshenko梁公式考虑了横向剪切变形.因此,它能够模拟较薄或较厚的梁.本章对Timoshenko梁的静力弯曲、自由振动和屈曲进行了分析.
10.Timoshenko梁的静力分析-Formulation
本文来自博客园，作者：FE-有限元鹰，转载请注明原文链接：https://www.cnblogs.com/aksoam/p/18133331
