《空间三角面片对相交判断算法》的matlab实现_ 0.2微秒

function [flag] = InsectTriPatch(T1,T2)
% 判断两个空间三角形面片是否相交    
% T1=[0 0 0;
    %     2 0 0;
    %     0 1.5 0;
    %     0 0 1];
    % T2=[0 0 -1;
    %     2 0 -1;
    %     0 2 -1;
    %     0 0 1];
    
    % 出自：《空间三角面片对相交判断算法》
    %   T=[A;B;C;n]
    %   A=[x y z]
    A1=T1(1,:);  % A1点的坐标：[x y z]
    B1=T1(2,:);
    C1=T1(3,:);
    n1=T1(4,:);
    
    A2=T2(1,:);
    B2=T2(2,:);
    C2=T2(3,:);
    n2=T2(4,:);
    
    %判断T2的3个顶点是否在平面π１ 同侧
    A1A2=A2-A1;
    A1B2=B2-A1;
    A1C2=C2-A1;
    temp1=[dot(A1A2,n1) dot(A1B2,n1) dot(A1C2,n1)];
    %判断T1的3个顶点是否在平面π2同侧
    A2A1=A1-A2;
    A2B1=B1-A2;
    A2C1=C1-A2;
    temp2=[dot(A2A1,n2) dot(A2B1,n2) dot(A2C1,n2) ];
    
    % 判断temp1 或 temp2 是否同号
    if any([all(temp1<0) all(temp1>0) all(temp2<0) all(temp2>0)])
        % T1,T2 不相交，return 0
        flag=0;
        return
    else
        if all([isequal(cross(n1,n2),[0 0 0]),isequal(temp1,[0 0 0])])
            % T1和 T2共面
            if  DetectVertexInTri(T1,T2)
                % 存在T1的顶点在T2内部或者存在T2的顶点在T1内部,判定T1、T2相交, 返回真
                flag=1;
                return
            else
                if DetectVertex(T1,T2)
                    flag=1;
                    return
                else
                    flag=0;
                    return
                end
            end
        else
            % T1 T2异面
            if any([EdgeInsectTri(T1,T2) EdgeInsectTri(T2,T1)])
                %存在 T２ 边与 T１ 相交或存在 T１ 的边与 T２相交
                flag=1;
                return
            else
                flag=0;
                return
            end
        end
    end
end

function is_in= PointInTri(T1,P)
% 函数实现： 判断一点是否在三角形T1内
    %   T=[A;B;C;n]
    %   A=[x y z]
    A1=T1(1,:);  % A1点的坐标：[x y z]
    B1=T1(2,:);
    C1=T1(3,:);
    n1=T1(4,:);
    
    A1B1=B1-A1;
    A1C1=C1-A1;
    B1C1=C1-B1;
    B1A1=A1-B1;
    C1A1=A1-C1;
    C1B1=B1-C1;
    
    A1P=P-A1;
    B1P=p-B1;
    C1P=P-C1;
    
    k1=dot(dot(A1P,cross(A1B1,n1)),dot(A1C1,cross(A1B1,n1)));
    k2=dot(dot(B1P,cross(B1C1,n1)),dot(B1A1,cross(B1C1,n1)));
    k3=dot(dot(C1P,cross(C1A1,n1)),dot(C1B1,cross(C1A1,n1)));
    
    if any([k1 k2 k3]<0)
        % k1 k2 k3 存在负值，则P不在T1中
        is_in=0;
        return
    else
        is_in=1;
    end
end

function flag = DetectVertexInTri(T1,T2)
% 比较：存在T１ 的顶点在 T２ 内部或者存在 T２ 的顶点在T１ 内部？
% loop T1
    for i=1:3 
        if PointInTri(T2,T1(i,:)) 
            % 说明T1的顶点在T2内部,T1,T2 相交,return 1
            flag=1;
            return
        end
    end
    % loop T2
    for i=1:3 
        if PointInTri(T1,T2(i,:)) 
            % 说明T2的顶点在T1内部,T1,T2 相交,return 1
            flag=1;
            return
        end
    end
end

function flag=fun2(T2,p1,p2,n)

    A2=T2(1,:);
    B2=T2(2,:);
    C2=T2(3,:);

    h1=dot(A2-p1,cross(p2-p1,n));
    h2=dot(B2-p1,cross(p2-p1,n));
    h3=dot(C2-p1,cross(p2-p1,n));
    temp=[h1 h2 h3];
    if any([all(temp<0) all(temp>0)])
        flag=0;
    else
        flag=1;
    end
end

function flag=DetectVertex(T1,T2)
    % 共面-步骤二
    %   T=[A;B;C;n]
    %   A=[x y z]
    % A1点的坐标：[x y z]
    n1=T1(4,:);
    n2=T2(4,:);

    index=[1 2;2 3;3 1];
    % T2的3个顶点
    for i=1:3
        if fun2(T2,T1(index(i,1),:),T1(index(i,2),:),n1)
            flag=1;
        else
            %有一条边不符合要求，直接返回0，不相交。
            flag=0;
            return
        end
    end
    % T1的3个顶点
    for i=1:3
        if fun2(T1,T2(index(i,1),:),T2(index(i,2),:),n2)
            flag=1;
        else
            %有一条边不符合要求，直接返回0，不相交。
            flag=0;
            return
        end
    end
    flag=1;
end

function flag= EdgeInsectTri(T1,T2)
% 函数实现：判断T2的线段A2B2 B2C2 C2A2是否与三角面片T1相交
    index=[1 2;2 3;3 1];
    tf=0;
    for i=1:3
        if fun3(T2(index(i,1),:),T2(index(i,2),:),T1)
            % 存在线段和面片相交
            flag=1;
            return
        else
            tf=0;
        end
    end
    flag=tf;
end

function flag=fun3(p1,p2,T1)
% 实现：判断边p1p2是否与T1相交
    %   T=[A;B;C;n]
    %   A=[x y z]
    A1=T1(1,:);  % A1点的坐标：[x y z]
    B1=T1(2,:);
    C1=T1(3,:);
    n1=T1(4,:);
    
    s1=cross(p1-A1,n1);
    s2=cross(p2-A1,n1);

    if all([s1==[0 0 0] s2==[0 0 0]])
        % p1p2和T1共面 
        if any([PointInTri(T1,p1) PointInTri(T1,p2)])
            % p1 p2，至少一个点在三角形T1中，则p1p2和T1相交
            flag=1;
            return
        else
            flag=0;
            return
        end
    else
        % p1p2和T1异面
        if dot(s1,s2)>0
            % P1P2在T1同侧, 判定不相交;
            flag=0;
            return
        else
            g1=dot(dot(p2-A1,cross(B1-A1,p1-A1)),dot(C1-A1,cross(B1-A1,p1-A1)));
            g2=dot(dot(p2-B1,cross(C1-B1,p1-B1)),dot(A1-B1,cross(C1-B1,p1-B1)));
            g3=dot(dot(p2-C1,cross(A1-C1,p1-C1)),dot(B1-C1,cross(A1-C1,p1-C1)));

            if all([g1>0 g2>0 g3>0])
                % g1 g2 g3 的计算结果均为非负,p1p2和T1相交
                flag=1;
                return
            elseif any([g1<0 g2<0 g3<0])
                % g1 g2 g3 的计算结果存在负值,p1p2和T1不相交
                flag=0;
                return
            end
        end
    end
end

测试代码：

T1=[71.9139   48.8001   56.5830 ;
     62.3056   73.4288   70.6124;
      52.5847   7.1895   57.6345;
      ];

T2=[93.0718   68.6186   21.6408 ;
    27.4472   1.6631   85.5462 ;
    6.2035   83.9585   95.9391];
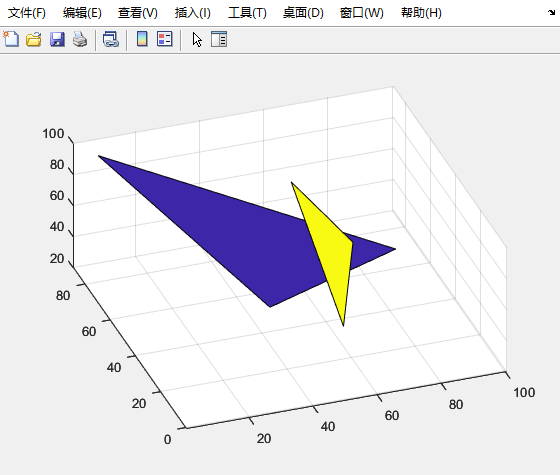
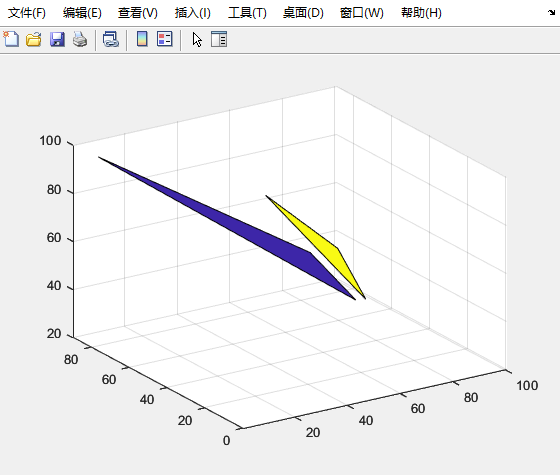
% plot triangles
v=[T1;T2];
f = [1 2 3;
    4 5 6];
patch('Faces', f, 'Vertices', v, 'FaceVertexCData',[1; 0] ,'FaceColor', 'flat');

% caculate norm vector
n1=cross(T1(2,:)-T1(1,:),T1(3,:)-T1(1,:));
n1=n1/norm(n1);
T10=[T1;n1];

n2=cross(T2(2,:)-T2(1,:),T2(3,:)-T2(1,:));
n2=n2/norm(n2);
T20=[T2;n2];

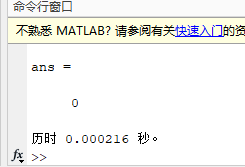
tic
InsectTriPatch(T10,T20)
toc