【Matlab】判断点和多面体位置关系的两种方法实现

合集 - 数值计算(18)
1.【数学公式】mathtype和word2016集成2.【MathType】word2016数学公式编号3.【Matlab】基于KDtree的最近邻搜索和范围搜索
4.【Matlab】判断点和多面体位置关系的两种方法实现
5.《空间三角面片对相交判断算法》的matlab实现_ 0.2微秒6.Mpmath库-学习笔记7.有限元方法[Matlab]-笔记8.结构动力学教材-学习笔记9.复合材料力学基础及有限元分析10.【数值计算方法】数值积分&微分-python实现11.【数值计算方法】2&3维高斯积分的python实现12.【数值计算方法】线性方程组的迭代解法13.【数值计算方法】线性方程组迭代算法的Python实现14.【数值计算方法】线性方程组的迭代解法-数值实验15.【数值计算方法】非线性方程求根16.【数值计算方法】非线性方程求根-数值实验17.【数值计算方法】常微分方程初值问题的数值解18.Note_Fem边界条件的处理和numpy实现的四种方法
收起

分别是向量判别法（算法来自他人论文）、体积判别法（code 是我从网上找的）。

方法一： 向量判别法

方法来自一会议论文：《判断点与多面体空间位置关系的一个新算法_石露》2008年,知网、万方、百度学术有收录。
优点：

  • 适合任意多面体
  • 计算简单
  • 速度快

算法原理

img

Matlab 实现

主函数为InPolyhedronByVJM(Nodes,P),当前仅支持ABAQUS 四面体和五面体单元，其余有需要的可自行在switch语句添加函数。
输入：

  • Nodes：包含节点顺序和坐标的N x 3的矩阵
  • P：1x3的行向量

这是我根据ABAQUS单元规则编写的函数，因此其他软件的网格信息文件还需要重写。

function flag = InPolyhedronByVJM(Nodes,P)
% 根据向量判别法，判断点和多面体的位置关系.
% 算法依据：石露,白冰,李小春. 判断点与多面体空问位置关系的一个新算法[C].
% 输入：
%       + Nodes: n x 3 matrix
%       + P    : 1 x 3 row vector
% 单元节点顺序需要满足ABAQUS的约定。
% Nodes是一个n x 3的数值矩阵，每一行表示多面体的一个节点的空间坐标。
% 点在多面体内部的充分必要条件：每个face上任一点到点P的向量和该face法向量的数量积都
% 小于等于0，否则在体外。
NumOfNode = size(Nodes, 1);
switch NumOfNode
    case 4
        flag = InTetrahedron(Nodes, P);
        disp('tetra')
    case 5
        flag = InPyramid(Nodes, P);
        disp('parymid')
end
end

针对C3D4类单元的判别函数

function flag = InTetrahedron(Nodes, P)
% tetra elem have 4 face.
% ABAQUS rule about node ordering and face numbering on element
FaceIDX = [1 2 3;
    1 4 2;
    2 4 3;
    3 4 1];
for faceId = 1 : 1 : size(FaceIDX, 1)
    % judge face i: node 1-node 2-node 3 face
    % get face normal vector(outside)
    n = -1 .* GetNormVector(Nodes(FaceIDX(faceId, 1), :), Nodes(FaceIDX(faceId, 2), :), Nodes(FaceIDX(faceId, 3), :));
    % calculate dot product of P and normal vector n
    N1P = P - Nodes(FaceIDX(faceId, 1), :);
    f = dot(N1P, n);
    if f > 0
        flag = 0;
        return
    end
end
flag=1;
end

针对C3D5类单元的判别函数

function flag = InPyramid(Nodes, P)
% Pyramid elem have 5 face.
% ABAQUS rule about node ordering and face numbering on element
FaceIDX = [1 2 3 4;
    1 5 2 0;
    2 5 3 0;
    3 5 4 0;
    4 5 1 0];
for faceId = 1 : 1 : size(FaceIDX, 1)
    % judge face i: node 1-node 2-node 3 face
    % get face normal vector(outside)
    n = -1 .* GetNormVector(Nodes(FaceIDX(faceId, 1), :), Nodes(FaceIDX(faceId, 2), :), Nodes(FaceIDX(faceId, 3), :));
    % calculate dot product of P and normal vector n
    N1P = P - Nodes(FaceIDX(faceId, 1), :);
    f = dot(N1P, n);
    if f > 0
        flag = 0;
        return
    end
end
flag = 1;
end

求面法向向量的函数

function NormalVector = GetNormVector(p1, p2, p3)
% function return a Normal Vector,base on RightHand Rule, according to three point (row vector)
% NormalVector=cross product of (p2-p1) and (p3-p1)
% check
if (~isrow(p1)) || (~isrow(p2)) || (~isrow(p3))
    return
end
p1p2 = p2 - p1;
p1p3 = p3 - p1;
NormalVector = cross(p1p2, p1p3);
end

附：abqus四面体和五面体单元的节点约定
img

img

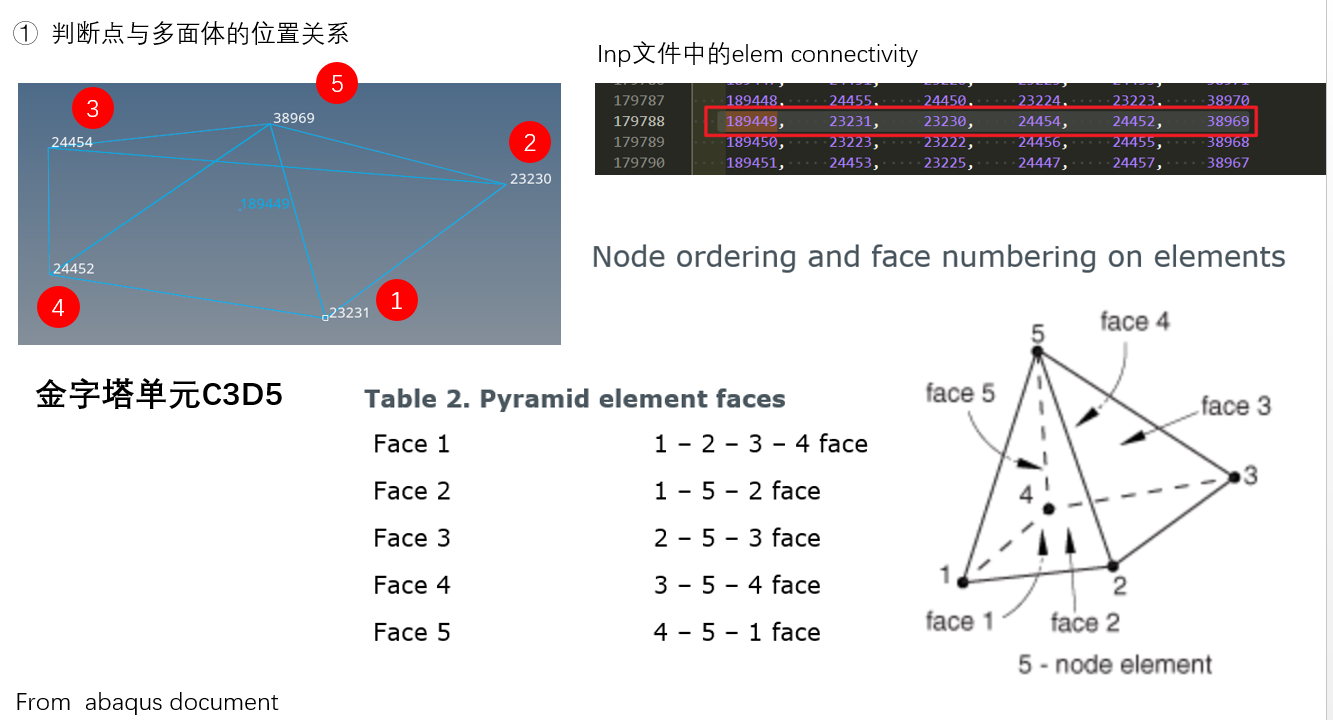
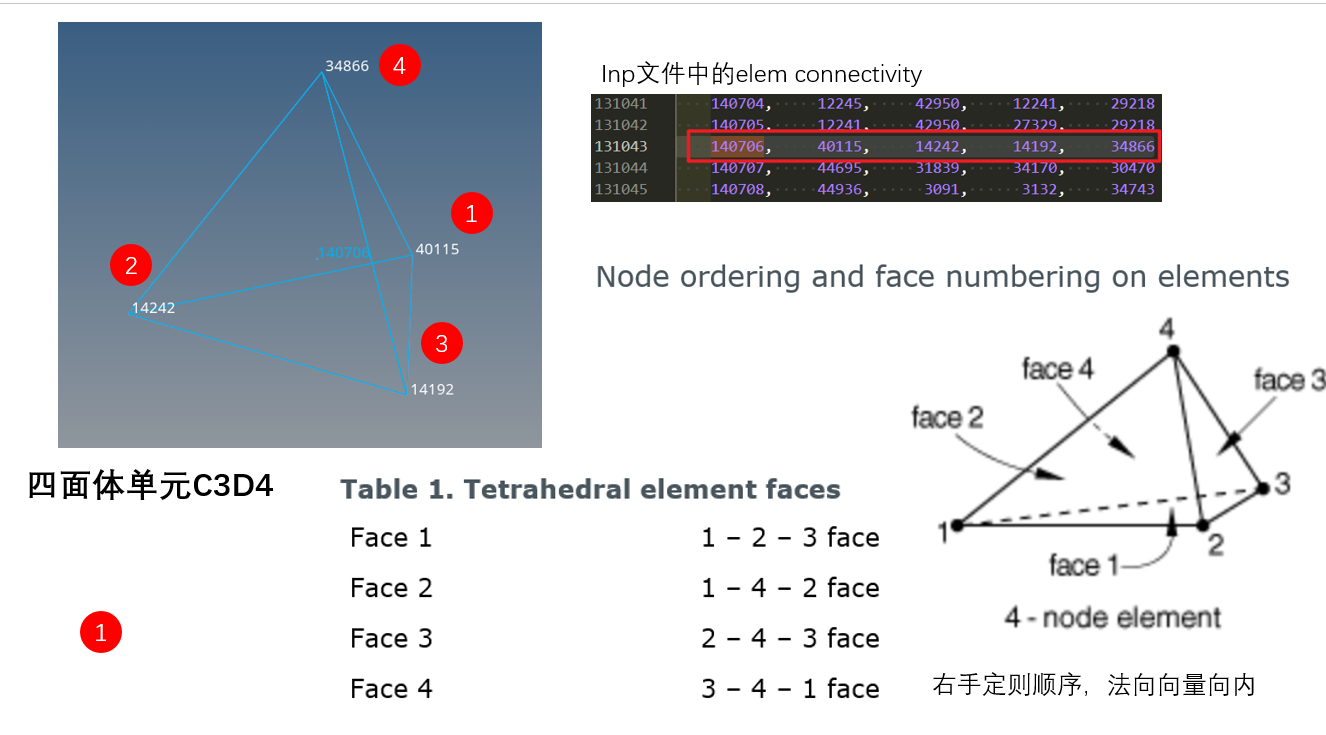
测试Matlab的速度和准确度

%% vector judge method test tetra elem (not include)
Nodes = [40033.883285119,  264.5168630711 ,  460.70942035982;
    40038.586165682,  269.82366853938,  464.20374836087;
    40032.364670267,  268.77493858153,  464.18513138978;
    40035.61509136 ,  262.38393588741,  466.45744915188];
P = sum(Nodes)/4+[100 0 0];
tic
disp('vector judge method test tetra elem(not include)')
flag = InPolyhedronByVJM(Nodes, P);
disp(flag)
toc
clear
%% volume judge method test tetra elem (not include)
Nodes = [40033.883285119,  264.5168630711 ,  460.70942035982;
    40038.586165682,  269.82366853938,  464.20374836087;
    40032.364670267,  268.77493858153,  464.18513138978;
    40035.61509136 ,  262.38393588741,  466.45744915188];
P = sum(Nodes)/4+[100 0 0];
tic
disp('volume judge method test tetra elem(not include)')
flag = inpolyhedronByVolCal(Nodes, P);
disp(flag)
toc
clear
%% vector judge method test tetra elem (include)
Nodes = [40033.883285119,  264.5168630711 ,  460.70942035982;
    40038.586165682,  269.82366853938,  464.20374836087;
    40032.364670267,  268.77493858153,  464.18513138978;
    40035.61509136 ,  262.38393588741,  466.45744915188];
P = sum(Nodes)/4;
tic
disp('vector judge method test tetra elem(include)')
flag = InPolyhedronByVJM(Nodes, P);
disp(flag)
toc
clear
%% volume judge method test tetra elem (include)
Nodes = [40033.883285119,  264.5168630711 ,  460.70942035982;
    40038.586165682,  269.82366853938,  464.20374836087;
    40032.364670267,  268.77493858153,  464.18513138978;
    40035.61509136 ,  262.38393588741,  466.45744915188];
P = sum(Nodes)/4;
tic
disp('volume judge method test tetra elem(include)')
flag = inpolyhedronByVolCal(Nodes, P);
disp(flag)
toc
clear
%% vector judge method test parymid elem
% node connectivity satisfy abaqus rule 
Nodes = [40074.01489458, 184.27859731629, 355.37056669335;
    40081.032227826, 179.72253222636, 357.32796879472;
    40080.400160415, 184.49866619658, 366.02835222196;
    40073.363546048, 189.104242665, 363.93134923301;
    40077.379811862, 179.07892353029, 363.81547779482; ];
P = [40077.2381281462+100	183.336592386904	361.294742947572];
tic
disp('test parymid elem')
flag = InPolyhedronByVJM(Nodes, P);
disp(flag)
toc
clear

img

方法二：体积判别法

这个代码是我在网上找的，出处已经忘了。

Matlab实现(仅限四面体)

function inflag = inpolyhedronByVolCal(points_mat, p_detected)
% input:
%     + points_set : 4 point's x y z coordinate,integrated in a 4X3 matrix
%     + p_detected : a point needed to detect ,1X3 matrix contain x y z
%                    coordinate
% return : inflag: 0 or 1
D0 = det([points_mat(1, :) 1;
    points_mat(2, :) 1;
    points_mat(3, :) 1;
    points_mat(4, :) 1]);
D1 = det([p_detected 1;
    points_mat(2, :) 1;
    points_mat(3, :) 1;
    points_mat(4, :) 1]);
D2 = det([points_mat(1, :) 1;
    p_detected      1;
    points_mat(3, :) 1;
    points_mat(4, :) 1]);
D3 = det([points_mat(1, :) 1;
    points_mat(2, :) 1;
    p_detected      1;
    points_mat(4, :) 1]);
D4 = det([points_mat(1, :) 1;
    points_mat(2, :) 1;
    points_mat(3, :) 1;
    p_detected      1]);
 
if (D0 < 0 && D1 < 0 && D2 < 0 && D3 < 0 && D4 < 0) || ((D0 > 0 && D1 > 0 && D2 > 0 && D3 > 0 && D4 > 0))
    inflag = 1;
else
    inflag = 0;
end
end
posted @   FE-有限元鹰  阅读(324)  评论(0)  编辑  收藏  举报
相关博文：
·  《空间三角面片对相交判断算法》的matlab实现_ 0.2微秒
·  【基础知识笔记】004 matlab-矩阵和数组的关系
·  计算几何笔记
·  JAVA PTA 大作业2
·  判断点与多边形的关系（4）：射线法
阅读排行：
· 25岁的心里话
· 闲置电脑爆改个人服务器（超详细） #公网映射 #Vmware虚拟网络编辑器
· 零经验选手，Compose 一天开发一款小游戏！
· 通过 API 将Deepseek响应流式内容输出到前端
· AI Agent开发，如何调用三方的API Function，是通过提示词来发起调用的吗
点击右上角即可分享
微信分享提示