ABAQUS-循环对称条件的详解

概括

anlysis of model that exhibit cyclic symmetry

循环对称分析技术用于Standard求解器。

  • makes it possible to analyze the behavior of a 360° structure with cyclic symmetry based on a model of a repetitive sector;
  • 可以在静态、准静态、热传递分析中确定循环对称加载的响应。
  • 可以计算360°结构的所有特征频率和特征模态（借助block Lanczos eigenfrequency extraction procedure）
  • 在基于模态的稳态动力分析中，可以确定对应于给定环对称模态的加载响应;
  • 对称表面上不要求匹配的网格。

Introduction

针对循环对称的结构，ABAQUS提供了一个技术减少计算消耗，通过分析其中一个重复单元（部分）。比如某结构有16个重复部分，那么就可以用45°的模型（包括2个重复单元）来分析。当然也可以分析22.5°的模型，这样计算效率更高。但这并不是必须的。

在这种分析中必须考虑两种基本情况:

  1. 初始状态下结构循环对称、且响应是循环对称的。
  2. 初始状态下结构循环对称、但响应是非循环对称的。

对于第一种情况，ABAQUS/STANDARD求解器支持具有循环对称响应的循环对称结构进行非线性、线性分析。在这种情况下只能施加循环对称荷载

整个分析过程中，结构是循环对称的，因此在load 中，结构在任何时候都不可能有任何非对称变形。所以只能施加循环加载。

对于第二种情况，需要额外的处理。这种情况只能执行线性摄动分析步。这是因为非对称变形响应使得“基态循环对称”的假设在后续一般非线性分析步中不成立了。如图1所示的循环对称结构的完全响应可以等于几个独立基响应(原文： basic response)的线性组合，每个基响应都对应于某个k-fold对称模式。

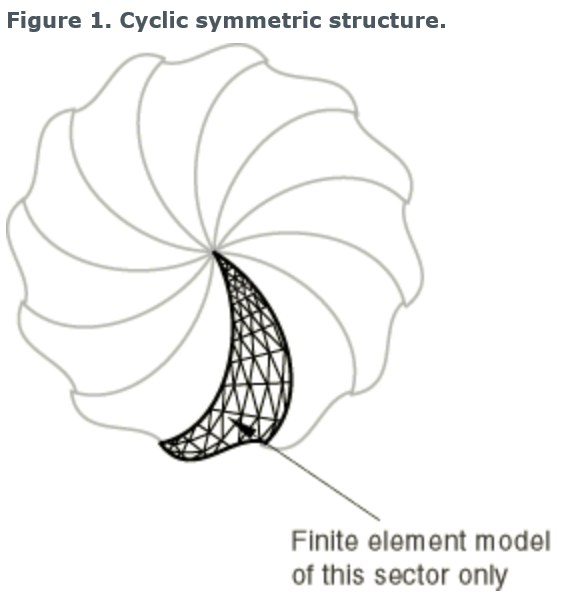
image-20230717193241833

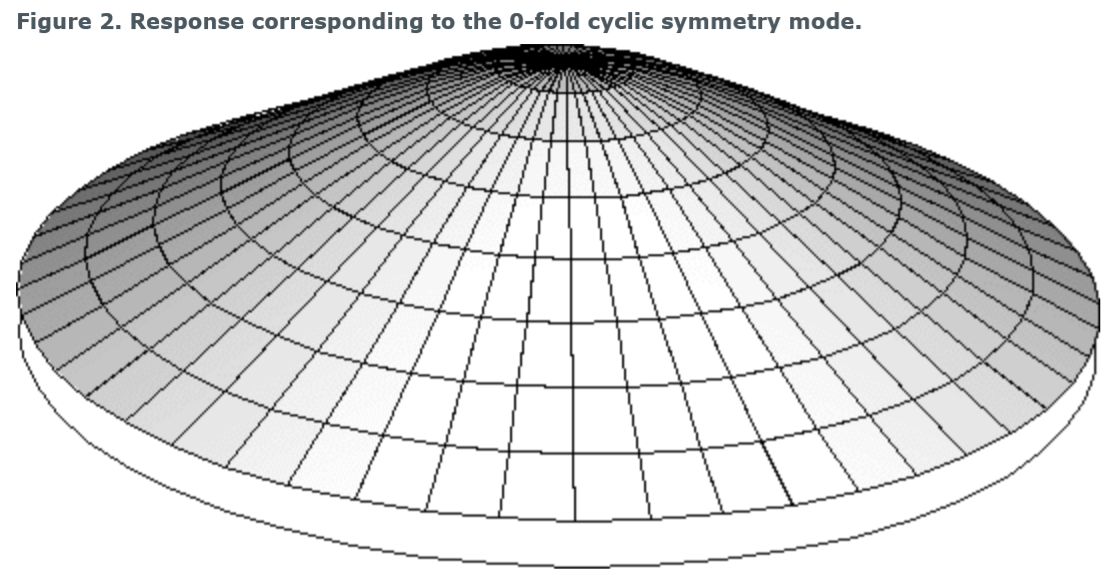
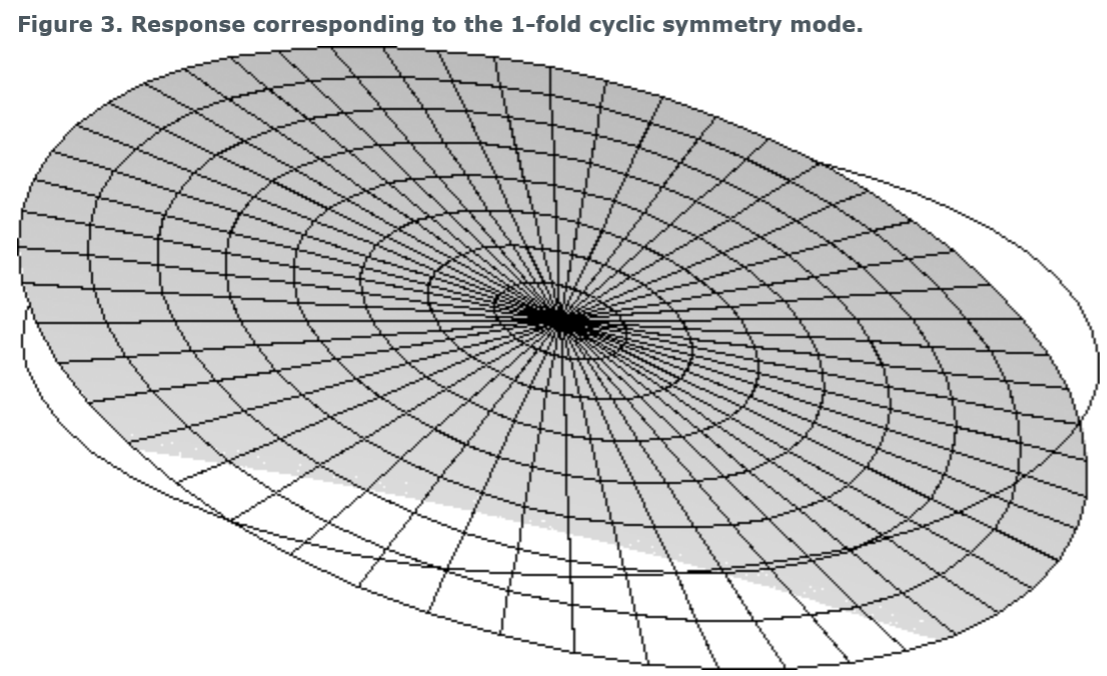
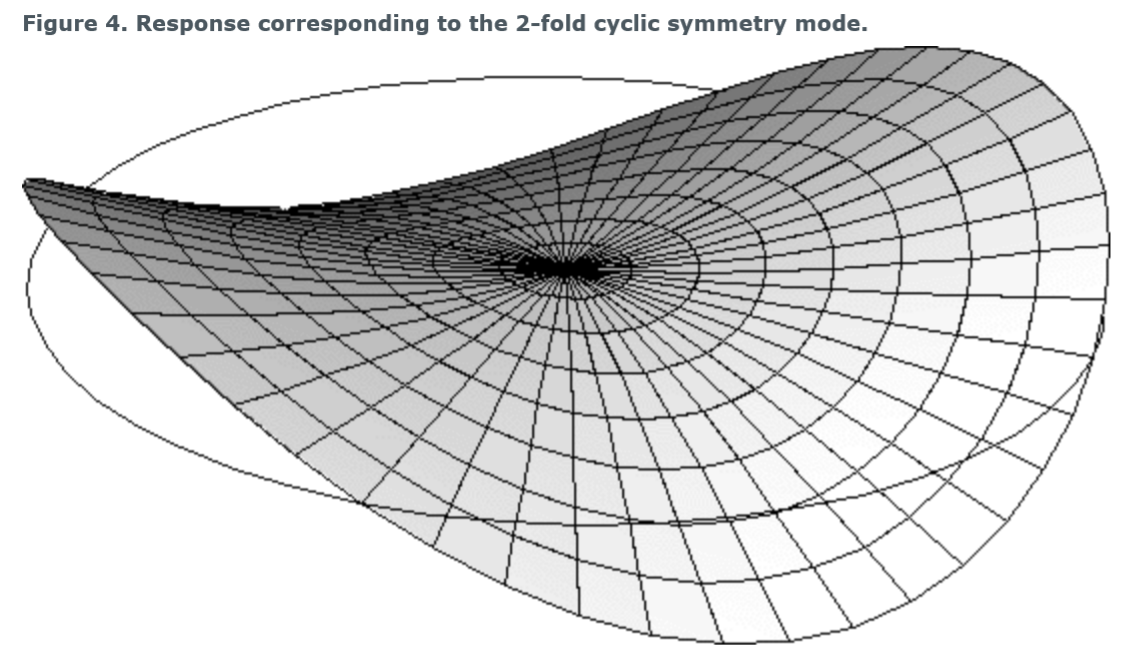
cyclic symmetry mode number,有时也称为“nodal diameter”,表示为一个基响应中沿着圆周的波数。图2、图3和图4说明了在包含四个重复扇区的循环对称结构中对应于0、1和2-fold模式(节点直径为0、1和2)的基本响应。

关于K-fold的理解，应该是指可以折叠多少次，就像折纸一般。图2中的响应，没法”折叠“，也就对应于0 -fold cyclir symmtry mode; 图3的响应可以折叠一次，过中心轴的对称平面只有一个，图三的响应有两个对称平面多中心轴且相互垂直。

一个完整的线性摄动分析可以通过求解一系列相应的线性分析来实现。单个重复单元上的循环对称边界条件给出了Hermitian 刚度矩阵和质量矩阵（是一个复数矩阵，具有对称实部和偏对称虚部）。序列中的第k次线性分析会使用与结构响应的k-fold 循环对称模态相对应的对称条件进行求解。对于N-fold循环对称的结构(N应该是指重复sector的数量)，需要的分析次数为：

\[N=偶数，分析次数=N/2+1\\ N=奇数，分析次数=(N+1)/2\\ \]

这样就能以相对较低的计算成本求解完整响应。

image-20230717202122389

image-20230717202136600

image-20230717202156735

To perform a general linear analysis of a cyclic symmetric structure，外部力应表示为基载荷（basic loads）的线性组合。每一个基载荷对应一个对称模态，并且激励产生了对应于同一模态的结构响应。在静态分析中，还没有实现在0倍模式以外的任何模式下定义负载的功能

由于0倍模态的响应保持循环对称性，这种类型的结构分析可以在一般的非线性分析步中完成，也可以在线性摄动步骤中完成(如上所述)。基于同样的原因，这样的阶跃可以作为循环对称线性摄动阶跃的预加载阶跃。

在ABAQUS2020中只有eigenfrequency extraction analysis(使用block Lancos方法)和 frequency domain, modal-based steady-state dynamic analysis能提取循环对称结构的非对称响应；对于特定的循环对称模态、一组循环对称模态或所有的循环对称模态，可以提取对称和非对称特征模态对应的固有频率。这些固有频率可以在后续的稳态动力分析中使用。

在基于稳态模态的动态分析中，集中、分布和表面载荷可以被定义为投射到特定的循环对称模态上。在相同的稳态动力学步骤中，所有施加的载荷必须被投影到相同的循环对称模式上。这一限制意味着在给定的稳态动力学步长内，指定的循环对称模态必须是相同的。

Defining a cyclic symmetric model

需要确定的参数有：

  • 单个sector 的网格模型，它被称为"datum sector"，基准扇区。
  • 指定重复sector的数量，n;
  • 在全局坐标系下，指定对称轴上两个点，轴的方向是from first piont to second piont。扇区是以轴为中心逆时针方向编号的，基准扇区为扇区-1。对于二维模型，只需要给定轴上一点即可，默认轴方向为Z的正方向，因此，sectors就在x-y平面上编号。

对应的关键字是：*CYCLIC SYMMETRY MODEL, N=n

CAE中对应的是：Interaction module: Interaction->Create: Cyclic symmetry: Total number of sectors: n

使用循环对称约束

要使用循环对称约束，除了上面的参数，还需要在datum sector上定义一对或多对相应的surface，才可以在对应面之间使用循环对称的surface-base得到tie 约束。

第一个surface是slave surface,surface上的节点自由度会通过内部生成Multi-piont constraints来消除。第二个surface 是一个master surface。如果定义2对及以上的slave/master surface，那么所有surface pairs的从slave 到master 的旋转方向需要相同。(i.e., clockwise or counterclockwise).

image-20230719165331274

Using mismatched surface meshes

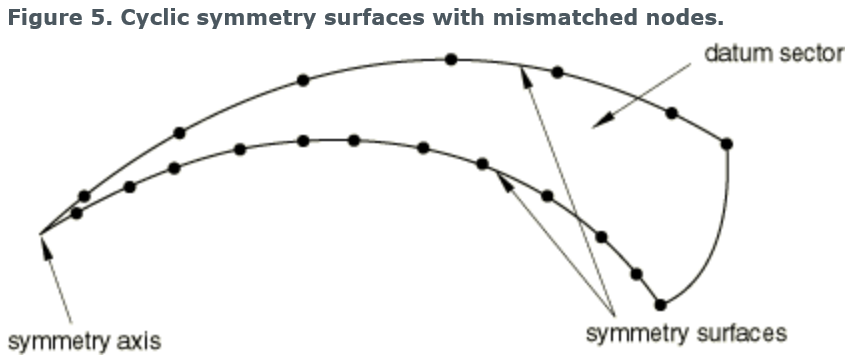
image-20230719165450006

上图就是mismatched surface meshes。较细的网格通常应该在slave表面。这种情况可能会导致应力场的局部不精确。

不准确性的大小取决于网格之间的不匹配程度以及所使用的元素类型

  • 二阶(修改)四面体单元的不准确性通常最为明显。

因此，在重点关注的区域，网格最好是匹配的。不匹配网格可以用在不关心的区域。

对于壳，循环对称条件必须应用于壳单元edge的节点。

ABAQUS2020循环对称约束不支持 element-based surfaces defined on the edges of shells

if mismatched meshes are used for shell elements, an element-based surface should be defined on the top or bottom of the shell elements adjacent to the edges that form the master surface. A node-based surface can be defined on the edge that forms the slave surface.

壳比较麻烦，所以更方便的做法就是使用matched mesh

Applying node-to-node cyclic symmetry constraints

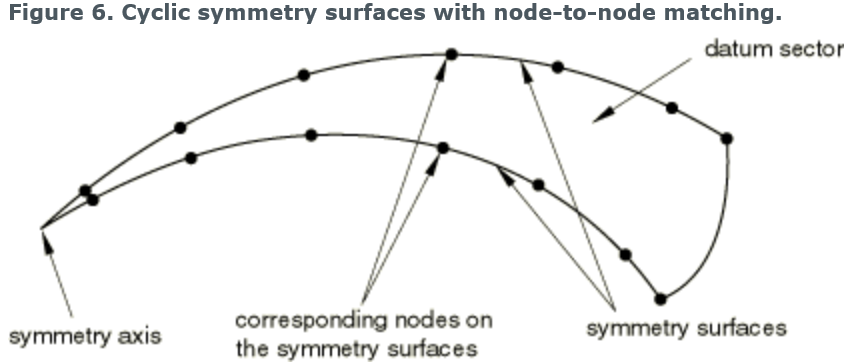
image-20230719170447986

如果使用的是matched mesh，哪个surface都可以是slave surface.

如上图中的mesh,这时尽可能使用node-based master surface来获得node-to-node cyclic symmetry constraints。好处：Abaqus/Standard会自动调整slave surface的节点位置从而与master surface的节点精确匹配。

这将产生最准确的结果，且计算成本最低。在这种情况下，从表面通常也会被选择为基于节点的表面，尽管计算上这并不重要，都会施加严格的节点到节点约束。

对于离散构件(如桁架或梁)，循环对称条件只能使用基于节点的曲面来执行。

image-20230719171655789

Applying cyclic symmetry conditions on the symmetry axis

如果节点位于对称轴上，则必须对0-fold和1-fold循环对称模态应用特殊的循环对称约束，而对其他循环对称模态则必须对所有自由度进行约束

对于0-fold循环对称模态，正交于对称轴平面的自由度受到约束;对于1-fold循环对称模态，沿对称轴的自由度是受限的。Abaqus/ standard将自动创建这些约束，只要节点包含在从曲面、主曲面或从曲面和主曲面的定义中

Obtaining all eigenfrequencies of a cyclic symmetric structure

循环对称结构的固有频率和特征模态可以使用基于Lanczos eigensolver的frequency step来提取。

No additional information is required for the eigenfrequency extraction procedure. All the natural frequencies are sorted in the conventional (ascending) order. For each natural frequency the cyclic symmetry mode number is reported.

有两种不同类型的特征模态：single and paired。

0-fold cyclic symmetry eigenmode 总是single的；如果N为偶数，那么N/2-fold cyclic symmetry eigenmode 也总是single的，剩下的N/2-1个(N为偶数)或者(N-1)/2个(N为奇数) cyclic symmetry eigenmode则是paired的。对应于paired eigenmode的固有频率是相等的且在dat文件中成对出现。

N=Total number of sectors

K-fold 循环对称eigenmodes(k<N/2在sector i=2…..N的展开式如下：

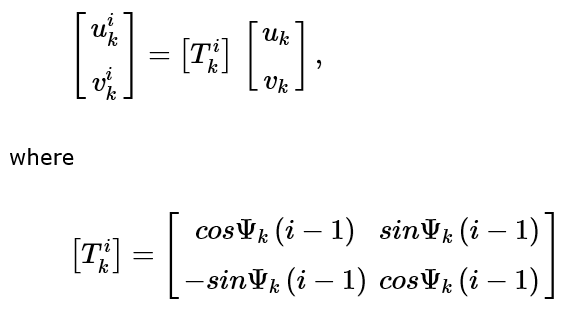
image-20230720141515897

上式中，\((u,v)和(u^i,v^i)\)是 paired eigenmodes corresponding to double natural frequencies on the first (datum) sector and on the ith sectors, respectively；\(\Phi_k=2\pi k/N\).

从以上的式子，0-fold 循环对称eigenmode总是对称的，比如，\(u^i_0=u_0\).类似的，N=偶数时，N/2-fold 循环对称eigenmode 也是单一的，因为\(u^i_{N/2}=(-1)^{(i-1)}u_{(N//2)}\)

这几个公式，我也有点迷糊。没完全明白，先从文档翻译过来再说。

Selecting the cyclic symmetry modes

循环对称边界条件是在model 的initial step上定义的。所以在后续的分析步中，可以通过指定要在分析中使用的最低循环对称模式\(n_{min}\)和要在分析中使用的最高循环对称模式\(n_{max}\)来选择将执行特征频率分析的循环对称模式。默认情况下：

\[n_{min}=0\\ n_{max}=N/2 or (N-1)/2 \]

n_min不能大于n_max; n_max不能大于N/2或N-1/2.If you do not select the cyclic symmetry modes, all possible cyclic symmetry modes are considered in the analysis. You can choose to use only the even cyclic symmetry modes.

image-20230720143929263

Selecting the cyclic symmetry mode for a steady-state dynamic step

Only a single cyclic mode can be excited in a steady-state dynamic step. You specify the cyclic symmetry mode associated with the loading in the load definition.

image-20230720144106556

Comparison of the cyclic symmetry analysis technique and MPC type CYCLSYM

MPC type CYCLSYM provides a subset of the functionality provided by the cyclic symmetry analysis capability. For an eigenvalue analysis MPC type CYCLSYM will allow extraction of the symmetric (0-fold) modes only. The cyclic symmetry analysis capability allows the use of surfaces to define the symmetry surfaces for the model, which enables the use of mismatched meshes on the symmetry surfaces, whereas MPC type CYCLSYM can be applied only on a node-to-node basis.

Limitations

存在以下限制:

  • 连续能力不可用于循环对称值提取过程。每个特征值提取步不会重复使用在前一个特征值提取步中获得的任何特征模式。
  • 对于定义在一个稳态动力学分析步内的loads，指定的cyclic symmetry mode 都必须相同
  • Base motion 不适用于cyclic symmetry models
  • Cyclic symmetry conditions被用于stress/displacement analysis 中的力学自由度和heat transfer analysis中的温度自由度；Cyclic symmetry conditions 不能用于 声压、pore pressure、 电学自由度。
  • Cavity radiation cannot be used in cyclic symmetric models

Initial conditions

所有使用的Initial conditions必须是循环对称的。

Boundary conditions

Only cyclic symmetric boundary conditions can be applied.

边界条件不能应用于slave循环对称surface上的节点

Loads

静态分析中，只有cyclic symmetric loads 可以施加。 Coriolis loads不能用。在频率分析中不考虑科里奥利力载荷刚度的影响。

在基于模态的稳态动力学中，load为特定cyclic symmetry mode在基准扇区上定义；对于k-fold cyclic symmetry mode(0<k<N/2),sector i（i=1…N）上的复载荷l = \(f^i+g^i\)(\(f^i,g^i分别为实部和虚部\))由下式得出：

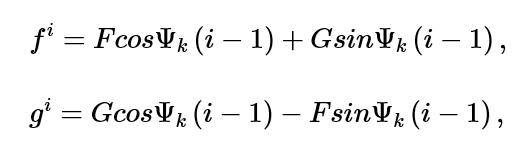
image-20230720210546818

其中，\(\Phi_k=2\pi k/N\) 。F和G 是基准扇区（datum sector ）上load的实部和虚部。

对于0-fold cyclic symmetry mode (k=0) ,这个类型的load 对应于\(f^i=F、g^i=G\)的循环对称载荷模型；对于k>0, 当空间恒定载荷pattern应用于旋转结构时(或恒定载荷pattern围绕结构旋转时)，this type of loading is generated.对于N/2-fold mode，sector i 的复载荷为： \(f^i=(-1)^{(i-1)}F、g^i=(-1)^{(i-1)}G\)

Predefined fields

Only cyclic symmetric predefined fields can be applied;the predefined fields should have the same values at each side of the datum sector.

Material options

for cyclic symmetry models of general procedures,没有特别限制；

频率分析步，具体要看Frequency Step 的要求

Elements

不能用轴对称单元

Output

节点位移和单元输出变量如应力、应变和截面力，仅适用于基准扇区；dat文件中列出的质量是为整个模型计算的。

在特征值提取过程中，需要满足以下特殊条件:

  • 如果选择位移特征向量归一化(默认值)，则在基准扇区上的每个特征向量中的最大位移条目是统一的。如果选择质量特征向量归一化，则对特征向量进行归一化，使在基准扇区上计算的广义质量是统一的。
  • dat文件中列出了特征值编号，循环对称模态编号和相应的频率(弧度/时间和周期/时间)，以及广义质量，复合模态阻尼因子，参与因子和模态有效质量。在基准扇区上重新计算广义质量;计算了整个模型的复合模态阻尼系数、参与系数和模态有效质量。
  • 可以通过给想要的output选择mode来限制输出到result 、dat文件
  • 用CAE可以为任意sector显示静态位移和特征模态; 基于模态的稳态动力学分析的结果可以显示任一sector，包括整个模型。

加深理解

abaqus帮助文档有一个关于循环对称条件的Example。看一下能加深理解。

链接：Abaqus Example Problems Guide (2016)---Analysis of a rotating fan using substructures and cyclic symmetry

fan_cyclicsymmodel_ss.inp

*HEADING
 Quarter model: FAN=HUB/4+BLADE    fan_cyclicsymmodel
 Cyclic symmetry model option and steady state dynamics
**
*RESTART,WRITE,FREQUENCY=1
**
** NODE DEFINITION: HUB/4+BLADE
** Nodes for the hub: 1--90 
**
*NODE
    1,   3.50000,   3.00000,   4.00000   
    3,   3.46638,   3.18024,   4.00000
    7,   3.18024,   3.46638,   4.00000
    9,   3.00000,   3.50000,   4.00000
**  
   28,   6.00000,   3.00000,   4.00000
   30,   5.79830,   4.08144,   4.00000
   34,   4.08144,   5.79830,   4.00000   
   36,   3.00000,   6.00000,   4.00000
**
   82,   6.00000,   3.00000,   0.00000
   84,   5.79830,   4.08144,   0.00000
   88,   4.08144,   5.79830,   0.00000         
   90,   3.00000,   6.00000,   0.00000
**
 9998,   3.00000,   3.00000,   4.00000
 9999,   3.00000,   3.00000,   0.00000
*NGEN,LINE=C,NSET=NHUB
 1,3,1,9998
 3,7,1,9998
 7,9,1,9998
*NGEN,LINE=C,NSET=RINGF
 28,30,1,9998
 30,34,1,9998
 34,36,1,9998
*NGEN,LINE=C,NSET=RINGB
 82,84,1,9999
 84,88,1,9999
 88,90,1,9999
*NFILL,NSET=HUB
 NHUB,RINGF,3,9
 RINGF,RINGB,6,9
**
** Total nodes for blade: 91--120, 
**     plus common nodes  57--61
**
*NODE,NSET=BLADE
   91,   6.34825,   4.61208,   2.00000
   92,   6.04542,   5.17363,   2.04275 
   93,   5.64799,   5.65929,   2.11107
   94,   5.16740,   6.05420,   2.19011
   95,   4.61648,   6.34954,   2.25973
   96,   6.97098,   5.04709,   2.00000
   97,   6.60952,   5.64419,   2.08975
   98,   6.14537,   6.18965,   2.22829
   99,   5.61424,   6.64337,   2.39622
  100,   5.04534,   6.97776,   2.55559
  101,   7.71735,   5.22982,   2.00000
  102,   7.23607,   5.92235,   2.13475
  103,   6.57818,   6.65456,   2.33376
  104,   5.87275,   7.29336,   2.58456
  105,   5.23136,   7.72660,   2.83877
  106,   8.44058,   5.48119,   2.00000
  107,   7.86154,   6.25188,   2.17913
  108,   7.04773,   7.13818,   2.43316
  109,   6.20063,   7.93303,   2.76013
  110,   5.49725,   8.45477,   3.10513
  111,   8.94199,   6.04637,   2.00000
  112,   8.35346,   6.80121,   2.24584
  113,   7.55742,   7.64823,   2.59979
  114,   6.73147,   8.41155,   3.04013
  115,   6.03050,   8.93642,   3.47975
  116,   8.88910,   6.78398,   2.00000
  117,   8.41737,   7.43225,   2.26100
  118,   7.89643,   8.00249,   2.59810
  119,   7.35361,   8.48209,   3.02957
  120,   6.78399,   8.88910,   3.50000
**
** NODE SETS
**
*NSET,NSET=XAXIS,GENERATE
 10,82,9
*NSET,NSET=YAXIS,GENERATE
 18,90,9
*surface,type=node,name=slave1
YAXIS,1.5
*surface,type=node,name=master1
XAXIS,1.5
*tie,cyclicsym,position=0.5,name=tie
 slave1,master1
*cyclic symmetry model,n=4
3., 3., 0.,  3., 3., 10.
*ELEMENT,TYPE=S4R
 1,1,10,11,2
*ELGEN,ELSET=HUB
 1,8,1,1,9,9,8
*ELEMENT,TYPE=S4R
 73,57,91,92,58
 77,91,96,97,92
*ELGEN,ELSET=CYLBLADE
 73,4,1,1
 77,4,1,1,5,5,4
**
*ELSET,ELSET=HUBF,GENERATE
   1,  24, 1
*ELSET,ELSET=HUBT,GENERATE
  25,  72, 1
**
*SHELL SECTION,ELSET=HUBF,MATERIAL=MAT
 0.250, 3
*SHELL SECTION,ELSET=HUBT,MATERIAL=MAT
 0.125, 3
*SHELL SECTION,ELSET=CYLBLADE,MATERIAL=MAT
 0.125, 3
*MATERIAL,NAME=MAT
*DENSITY
 7850.,
*ELASTIC,TYPE=ISOTROPIC
 2.E+11, 0.29
*NSET,NSET=NPRINT,GENERATE
 28,36,1
 55,63,1
**
*NSET,NSET=PRINT,GEN
116,120,1
*BOUNDARY
 NHUB,ENCASTRE
**
*STEP,nlgeom,INC=1000
 Step 1: centrifugal loading
*STATIC
 .1,1.
**
*DLOAD
 CYLBLADE, CENT, 6.3e6, 3., 3., 0., 0., 0., -1.
 HUBF, CENT, 6.3e6, 3., 3., 0., 0., 0., -1.
 HUBT, CENT, 6.3e6, 3., 3., 0., 0., 0., -1.
**
*EL PRINT,FREQ=0
*NODE FILE,FREQ=2,NSET=PRINT
U
*NODE PRINT,FREQ=0 
*NODE FILE,FREQ=0 
**
*END STEP
**
*STEP
** *FREQUENCY,eigensolver=lanczos
*FREQUENCY,eigensolver=lanczos,normalization=mass
 26,,,,8
*SELECT CYCLIC SYMMETRY MODES, NMIN=0, NMAX=0
*EL PRINT,FREQ=0
*NODE PRINT,FREQ=0
*MODAL FILE
*END STEP
*STEP
*STEADY STATE DYNAMICS,FREQUENCY SCALE=LINEAR,INTERVAL=RANGE
6.0,137.0,10,4.
*DLOAD, LOAD CASE=1, OP=NEW, CYCLIC MODE=0
 CYLBLADE, P, 6.3e6
 HUBF, P, 6.3e6
 HUBT, P, 6.3e6
*DLOAD, LOAD CASE=2, OP=NEW, CYCLIC MODE=0
 CYLBLADE, P, 6.3e6
 HUBF, P, 6.3e6
 HUBT, P, 6.3e6
*MODAL DAMPING,MODAL=DIRECT
 1,26,0.03
*SELECT EIGENMODES, GENERATE
1,26,1
*EL PRINT,ELSET=CYLBLADE,FREQUENCY=10
S11,E11
*NODE PRINT,NSET=PRINT,FREQUENCY=10
U, 
*NODE FILE,NSET=PRINT,FREQUENCY=10
U,V,A,RF
*MODAL PRINT,FREQUENCY=10
GU, 
GA, 
GPU, 
*EL FILE,ELSET=CYLBLADE,FREQUENCY=10
S, 
*OUTPUT,FIELD,FREQUENCY=999
*NODE OUTPUT,NSET=PRINT
U,V,A,RF
*ELEMENT OUTPUT,ELSET=CYLBLADE
S, 
*OUTPUT,HISTORY,FREQUENCY=10
*NODE OUTPUT,NSET=PRINT
U,V,A,RF
*ELEMENT OUTPUT,ELSET=CYLBLADE
S, 
*END STEP
*STEP
** *FREQUENCY,eigensolver=lanczos
*FREQUENCY,eigensolver=lanczos,normalization=mass
 56,,,,8
*SELECT CYCLIC SYMMETRY MODES, NMIN=1, NMAX=1
*OUTPUT, FIELD, FREQUENCY=0
*EL PRINT,FREQ=0
*NODE PRINT,FREQ=0
*NODE FILE,FREQ=0
*EL FILE,FREQ=0
*MODAL FILE
**
*END STEP
*STEP
*STEADY STATE DYNAMICS,FREQUENCY SCALE=LINEAR,INTERVAL=RANGE
6.0,137.0,10,4.
*DLOAD, LOAD CASE=1, OP=NEW, CYCLIC MODE=1
 CYLBLADE, P, 6.3e6
 HUBF, P, 6.3e6
 HUBT, P, 6.3e6
*DLOAD, LOAD CASE=2, OP=NEW, CYCLIC MODE=1
 CYLBLADE, P, 6.3e6
 HUBF, P, 6.3e6
 HUBT, P, 6.3e6
*MODAL DAMPING,MODAL=DIRECT
 1,26,0.03
*SELECT EIGENMODES, GENERATE
1,26,1
*EL PRINT,ELSET=CYLBLADE,FREQUENCY=10
S11,E11
*NODE PRINT,NSET=PRINT,FREQUENCY=10
U, 
*NODE FILE,NSET=PRINT,FREQUENCY=10
U,V,A,RF
*MODAL PRINT,FREQUENCY=10
GU, 
GA, 
GPU, 
*EL FILE,ELSET=CYLBLADE,FREQUENCY=10
S, 
*OUTPUT,FIELD,FREQUENCY=999
*NODE OUTPUT,NSET=PRINT
U,V,A,RF
*ELEMENT OUTPUT,ELSET=CYLBLADE
S, 
*OUTPUT,HISTORY,FREQUENCY=10
*NODE OUTPUT,NSET=PRINT
U,V,A,RF
*ELEMENT OUTPUT,ELSET=CYLBLADE
S, 
*END STEP
*STEP
** *FREQUENCY,eigensolver=lanczos
*FREQUENCY,eigensolver=lanczos,normalization=mass
 56,,,,8
*SELECT CYCLIC SYMMETRY MODES, NMIN=2, NMAX=2
*OUTPUT, FIELD, FREQUENCY=0
*EL PRINT,FREQ=0
*NODE PRINT,FREQ=0
*EL FILE,FREQ=0
*NODE FILE,FREQ=0
*MODAL FILE
**
*END STEP
*STEP
*STEADY STATE DYNAMICS,FREQUENCY SCALE=LINEAR,INTERVAL=RANGE
6.0,137.0,10,4.
*DLOAD, LOAD CASE=1, OP=NEW, CYCLIC MODE=2
 CYLBLADE, P, 6.3e6
 HUBF, P, 6.3e6
 HUBT, P, 6.3e6
*DLOAD, LOAD CASE=2, OP=NEW, CYCLIC MODE=2
 CYLBLADE, P, 6.3e6
 HUBF, P, 6.3e6
 HUBT, P, 6.3e6
*MODAL DAMPING,MODAL=DIRECT
 1,26,0.03
*SELECT EIGENMODES, GENERATE
 1,26,1
*EL PRINT,ELSET=CYLBLADE,FREQUENCY=10
S11,E11
*NODE PRINT,NSET=PRINT,FREQUENCY=10
U, 
*NODE FILE,NSET=PRINT,FREQUENCY=10
U,V,A,RF
*MODAL PRINT,FREQUENCY=10
GU, 
GA, 
GPU, 
*EL FILE,ELSET=CYLBLADE,FREQUENCY=10
S, 
*OUTPUT,FIELD,FREQUENCY=999
*NODE OUTPUT,NSET=PRINT
U,V,A,RF
*ELEMENT OUTPUT,ELSET=CYLBLADE
S, 
*OUTPUT,HISTORY,FREQUENCY=10
*NODE OUTPUT,NSET=PRINT
U,V,A,RF
*ELEMENT OUTPUT,ELSET=CYLBLADE
S, 
*END STEP
posted @ 2023-07-20 21:38  FE-有限元鹰  阅读(1441)  评论(0)  编辑  收藏  举报