【ABAQUS文档笔记】ABAQUS刚体单元和可变形单元的review

学习笔记，帮助文档学习笔记

目录

• A. finite element
  • • DOF of Elem
    • Order of Elem
    • Formulation of Elem
    • Integration
  • A.1 continuum element
    • DOF
    • elem property
    • Formulation and integration
    • 单元输出
  • A.2 Shell Element
    • elem library
    • dof
    • elem property
  • A.3 BEAM Element
    • dof
    • elem property
    • Formulation and integration
    • Element output variables
  • A.4 truss elem
• B.Rigid Body
  • • 什么时候使用刚体？
    • 刚体组件
    • rigid elements

---

abaqus 两大类单元：finite element 和 rigid body 。

• finite element is deformable.
• rigid body is umdeformable,
  1. 可以把一个实体或者实体的一部分定义为rigid body
  2. 可以赋予大多数单元类型
  3. 优势：只计算ref node上的6个dof ,所以计算成本低。

A. finite element

abaqus 有庞大的单元类型库，并且abaqus /explicit的单元库是abaqus/standard 的子集。

DOF of Elem

不同的单元类型有不同的自由度，如：stress/displacement analysis的单元为translate /rotation dof; heat transfers analysis 的单元自由度为 Temperature ;

如果不指定单元orientation ，那就会默认取global system 作为1- 2- 3- axis;

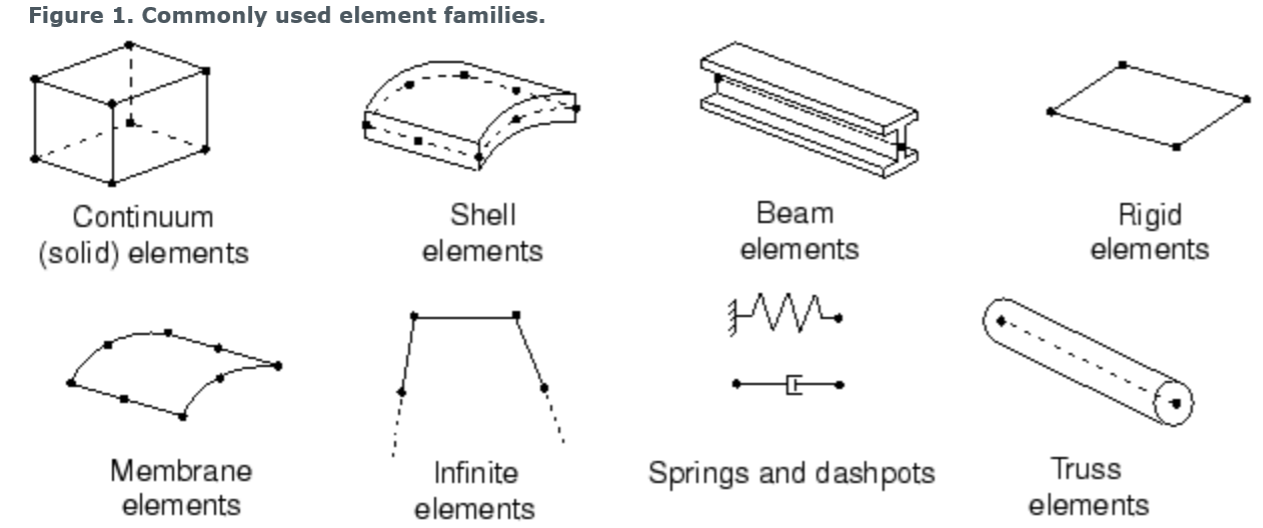
对于轴对称单元：

r direction 对应 1-axis
z direction 对应 2-axis

Order of Elem

Standard ：广泛支持一阶和二阶单元
Explicit : 只支持一阶单元(除了Quad Beam,Quad Tet,Modify Tet/tri)

Formulation of Elem

formulation 是和单元行为的数学理论有关的；
如果不采用adaptive mesh :

• 拉格朗日描述：材料和单元关联，并且不能流过（穿透单元的边界），一般用于描述固体力学
• 欧拉或粒子描述：单元在空间中固定，材料在其中流动，可以穿透单元边界，一般多用于计算流体力学

Abaqus/standard 可以用欧拉单元来模拟对流传热。自适应网格结合了纯拉格朗日和欧拉分析的特点，并允许运动的元素是独立的材料。

为了适应不同类型的行为，Abaqus某些单元族包含了几种不同形式的元素。例如，shell element系列有三个类：适合于一般shell分析的，针对薄壳的，针对厚壳的。

abaqus 的单元不仅有standard formulation ,还有 alternative formulation. assign elem type 的时候就可以选择。比如C3D8是标准的formulation，C3D8R/C3D8H是alternative formulation。

abaqus 有些formulation 可以求解多物理场耦合问题，比如C3D8T，具备mechanical and thermal 的自由度，即可以用于求解热力耦合问题。

Integration

Abaqus的数值技术可以对每个单元体积上的各种量进行积分。对大多数的单元，abaqus 可以用高斯积分求出单元积分点上的value.

abaqus 还可以决定积分是完全积分还是缩减积分，这对求解精度有着很大的影响。使用缩减积分的单元，一般以R或RH结尾。例如，
+ CAX4:4 节点，完全积分，线性，轴对称，固体单元。
+ CAX4R：则是CAX4的缩减积分版本。

ABAQUS/STANDARD 求解器支持完全积分和缩减积分的单元。
ABAQUS/EXPLICIT求解器只支持缩减积分的单元（也有一些例外）

A.1 continuum element

一般来说，continuum elem　可以对任何geometry建模，承受任意载荷。abaqus有stress/displacement,nonstructural, coupling field continuum elem。

continuum element name：

• 开头字母是C
• 第二第三个字母:
  • PE - a plane strain element
  • PS - a plane stress element.
  • 3D - an axisymmetric element
  • AX - a three-dimensional element

3D continuum element 可以是hexahedra (bricks), wedges, pyramids, or tetrahedra.
尽量使用六面体或者二阶四面体单元，一阶四面体单元C3D4 使用的是简单的，常应变的formulation，需要更高的网格密度才能得到精确解。

2D continuum element 有三角形和四边形。abaqus 有多种的2D continuum element 用于不同的out of plane behavior

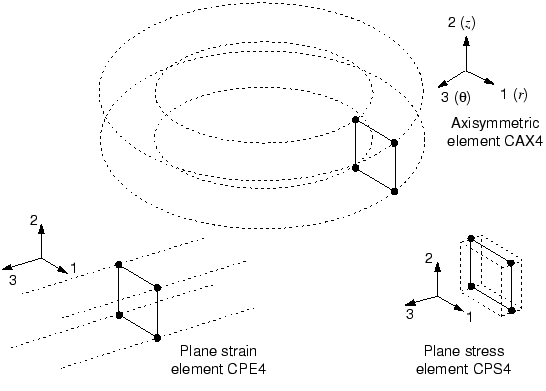
• plane strain elem assume : out-of plane strain (\(\epsilon_{33}\))为 0,
  • 可以模拟thick shell
• plane stress elem assume ：out-of-plane stress(\(\sigma_{33}\))为 0，
  • 适合模拟thin shell
• 轴对称单元没有扭转，适合模拟轴对称的结构，同时载荷也必须是轴对称的。

除了上面三种，abaqus还有广义平面应变单元（ generalized plane strain elements），扭转轴对称单元，轴对称变形的轴对称单元

• 广义平面应变单元包括了平面外应变，在法向上是线性的。特别适合用于厚截面的热应力分析
• 扭转轴对称单元，可以绕对称轴扭转。很适合模拟圆柱形结构(如轴对称橡胶衬套)的绕对称轴扭转。
• 具有不对称变形的轴对称元素建模最初可以不对称变形（通常是由于弯曲）的轴对称几何形状。他们是有用的模拟问题，如轴对称橡胶安装，是受到剪切载荷。这个是直接翻译的，原文我也没搞懂

DOF

3D continuum element 每个节点上的自由度为1 2 3；

plane strain elements, plane stress elements, and axisymmetric elements without twist 每个节点上的自由度为1 2；

elem property

all solid element 必须赋予solid section。section define by material and addtioinal geomtry data。

对于3D and axisymmetric element,不需要 额外的geomtry data;
plane stress and plane strain element 需要 定义shell thickness,default is 1 ；

Formulation and integration

略

单元输出

默认情况下，单元输出基于全局笛卡尔坐标系。
默认下，单元积分点上输出变量的方向

但是，如果不想基于全局坐标系输出，那你可以自定义一个local system。那么odb中的输出变量就基于local system了。在large-displacement simulation 中，local system 会随节点而旋转。

A.2 Shell Element

shell elems 有两种：

• continuum shell
• conventional shell

conventional shell 在单元形状上是2d的（三角形或者四边形）；continuum shell 但是在formulation & behavior上和convention shell 类似。

elem library

in abaqus/standard,3D shell有3钟formulation：general-purpose、thin-only、thick-only ,他么的一个区别是，general-purpose shell 可以模拟shell 在厚度的变化，而其他的shell element 都假定厚度不变

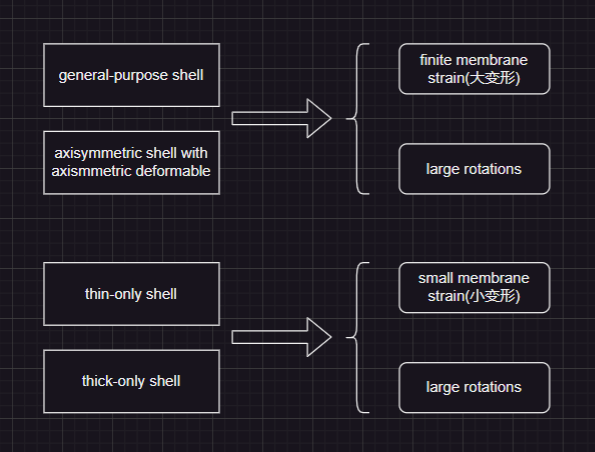
in abaqus/explicit, 只有general-purpose shell，但不管是finite membrane strain 或 small membrane strain 都可以模拟。在大多数的explicit 分析中，finite-strain-shell （S4 S4R S3 S3R）都是比较合适的，除非你能确定模拟过程中只发生small strain，不然别用S4RS等单元。

dof

• S4R5/STRI65——>5 dofs at each node;
• 轴对称shell——>3 dofs at each node;
• other shell——> 6 dofs at each node;

elem property

shell elem must refer to a shell section(thickness/material)
shell-cross-section's stiffness 的两种计算方式：

• once at begin of analysis

在前处理时就给定shell-cross-section的engineering constants,such as moment of interia, area,etc.这样会使求解器的计算更少。

• during analysus

abaqus 自动根据数值积分的手段在厚度上的积分点计算elem behavior ,材料可以时linear or nonlinear; 在定义shell section的时候，section intergation point 的个数必须是奇数

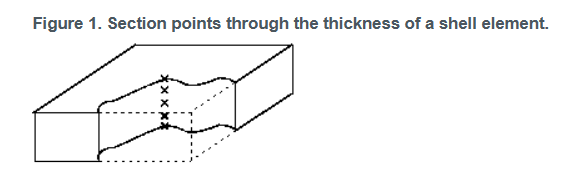
A.3 BEAM Element

beam 单元一般用来实现1D单元的建模（这种单元的特点是轴向维度显著大于其他两个方向）

dof

3D beam elem 在每个节点上有6个dofs（三个平动自由度和三个转动自由度）；

“open-section”类型的beam elem（如B31OS）会有一个额外的自由度7,表示cross-section的warp（翘曲）（这个单元只在Standard中可用）

2D beam elem 每个节点有3个dofs( 2个平动和一个转动)

elem property

all beam elem must refer to material and cross-section profile;

beam elem 的cross-section profile 两种定义方式：

• specify demension and shape of the section
• specify section's engineering prperties ,such as area,moment od interia;

不管是指定截面常数或是截面形状，abaqus 求解时需要的都是 面积，惯性矩，扭转常数等数据。还可以定义具有线性锥形截面的梁

Formulation and integration

linear beam and quadratic beam is suitable for modeling** 细长梁和粗壮梁；**
cubic beam elem（B23 B33） 基于small axial strain 和不考虑剪切变形，所以基本只适合细长梁的建模

standard求解器提供了适合 建模薄壁,开截面梁的单元，能够反映扭转效应（torsion effect）和开口截面的翘曲（warp of open-section）,比如I-section、U-section。

Element output variables

三维可剪切变形梁单元中的应力分量是轴向应力（\(\sigma_{11}\)）和扭转引起的剪切应力(\(\sigma_{12}\)).剪切应力作用于薄壁截面中的截面壁。还提供相应的应变测量。

剪切变形梁还提供了截面横向剪切力的估计值。Abaqus/Standard 中的细长（cubic）梁只有轴向变量作为输出。open-section beam 也只有轴向变量作为输出，因为在这种情况下扭转剪切应力可以忽略不计。

2D beam 只输出轴向应力和应变。

除此之外，还可以输出轴向力、弯矩和围绕局部梁轴的曲率

A.4 truss elem

truss是只承受拉压载荷的杆。不能抵抗弯曲，能有效建模销链接的结构；有时候也能用来近似模拟电缆或者绳子，比如在网球拍中。

truss elem 的节点自由度为U1 U2 U3或者U1 U2。只有平动自由度。 定义truss elem需要assign truss section,并且定义cross-section area.

如果杆的刚度远超整体结构的刚度，这时候用混合桁架单元更合适(hybrid truss element )

truss单元能输出轴向应力和应变

B.Rigid Body

abaqus 中，刚体的运动由reference node 决定。刚体动力学

什么时候使用刚体？

刚体是不可变形的component。一般用来model 刚度远远大于其他组件的部分、固定的或者是承受大刚体运动。比如在准静态成型模拟中，经常把冲头、滚轮等刀具假设为刚体。

刚体的形状定义有两种方法；一是旋转或拉伸二维草图，得到解析刚体表面；二是离散刚体，由网格和节点构成。

解析刚体无法mesh，离散刚体可以mesh。前者求解效率更高，但形状简单；后者求解慢些，胜在灵活。

刚体不会发生形状变化，但可以发生大的刚体运行。可以直接指定刚体的mass，inertia，也可以由软件自动计算（from elems）

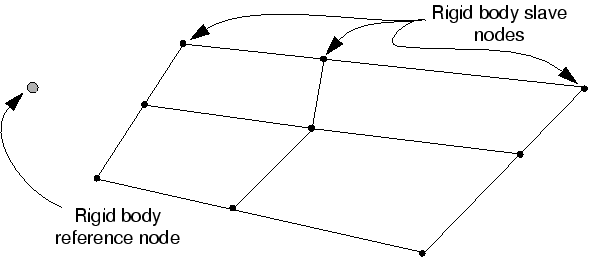
施加边界条件到参考点可以指定刚体的运动；刚体的load由施加在节点上的集中载荷和施加在单元上的分布载荷产生的。load也可以直接施加到参考点。

在分析复杂模型的时候，可以暂时将远离目标区域的部分模型设置为rigid body;之后再进一步分析完整模型。

刚体的最大优势是计算效率高，刚体运动完全由刚体参考节点的六个自由度决定。

在abaqus/explicit 求解器中，刚体和作为刚体部分单元不影响全局时间增量，在刚性区域使用刚体代替可变形单元，可以得到更大的全局时间增量，而不会显著影响解决方案的整体精度。

在接触分析中，用解析刚体面定义的刚体在计算成本方面比离散刚体稍微便宜一些，产生更平滑的结果。例如，在Abaqus/Explicit中，解析刚体的接触噪音往往比与离散刚体的接触噪音更小，因为解析刚体表面可以光滑，而离散刚体本质上是多面的。然而，可以用解析刚性表面定义的形状是有限的。

刚体组件

刚体的参考点决定了刚体运动，参考点有平动和转动自由度，每个刚体必须单独指定一个参考点。

参考点的位置并不重要。例外的是：

• 刚体绕某根轴旋转运动
• 关注刚体关于某根轴的力矩反作用力

这两种情况，参考点必须放在穿过刚体的轴上。

离散刚体还有一个组件：从节点。

离散刚体由一系列的nodes组成，在interaction 模块定义刚体约束的时候。指定了参考点，以及参考点控制的一部分elems和nodes。

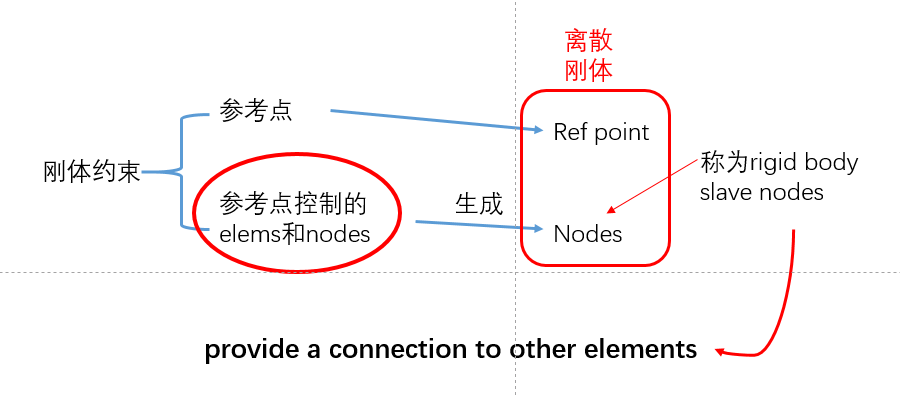
这些刚体从节点有两种类型：

• Pin nodes,只有平移自由度
• Tie nodes,具有平移和旋转自由度

刚体从节点类型由节点所附着的刚体的元素类型决定。

如果将节点直接分配给刚体时，也可以指定或修改节点类型。按我的理解就是：

• rigid body slave node's type==Pin nodes时，刚体参考点的运动只能约束这些节点U1 U2 U3自由度，从节点的平移自由度和参考点平移自由度运动一致
• rigid body slave node's type==Tie nodes时，刚体参考点的运动约束这些节点U1 U2 U3 UR1 UR2 UR3自由度，从节点的6个自由度和参考点6个自由度运动一致

从节点的类型可以由刚体单元类型决定，就不用深究slave node type了。

定义刚体的节点不能有任何边界条件、多点约束或约束方程。但是，可以将边界条件、多点约束、约束方程和载荷应用于刚体参考节点。

rigid elements

所有刚性元素的名称都以字母r开头。后面的字符表示元素的维度。例如，“2D”表示该元素是平面的;和" AX "表示元素是轴对称的。最后一个字符表示元素中的节点数。

三维四边形(R3D4)和三角形(R3D3)刚性单元可以对三维刚体的二维表面进行建模。双节点刚性单元可用于平面应变、平面应力和轴对称模型。

只有刚体参考节点具有独立的自由度。对于三维单元，参考节点具有三个平移自由度和三个旋转自由度;对于平面和轴对称元素，参考节点的自由度为1、2和6(绕3轴旋转)。

附着在刚性单元上的节点只有从属自由度。这些节点的运动完全由刚体参考节点的运动决定。对于平面和三维刚性元件，唯一的从属自由度是平移。Abaqus/Standard中的刚性梁单元与相应的变形梁单元具有相同的从自由度:三维刚性梁为1 - 6，平面刚性梁为1、2和6。

刚性元素的唯一输出是节点的运动。另外，在刚体参考节点处，可以得到反作用力和反力矩。