【Matlab】求解复合材料层合板刚度矩阵及柔度矩阵
1. matlab文件结构
2. main.m代码
clc
clear;
warning off;
%%
%铺层角度数组
angles=[0 90 0]; % °
%单层厚度
ply_thickness=0.125; %mm
%lamina 性能参数
E11=1000 ;%Mpa
E22=1000 ;
nu12=0.3 ;
G12=1500 ;
%%
% 铺层数量
ply_num=size(angles);
ply_num=max(ply_num);
% 求zlist,wQij等矩阵
% z坐标数组
zlist=Get_zlist(ply_thickness,angles);
% 所有ply的偏轴刚度矩阵(3 X 3 X k)
Q=Get_Qij(E11,nu12,E22,G12);
wQij=Get_wQij(Q,angles);
%%
% 求A B D刚度矩阵
%A Matrix
A=zeros(3,3);
for i=1:ply_num
temp=wQij(:,:,i).*(zlist(i+1)-zlist(i));
A=A+temp;
end
%A Matrix
B=zeros(3,3);
for i=1:ply_num
temp=0.5*wQij(:,:,i).*(zlist(i+1)^2-zlist(i)^2);
B=B+temp;
end
%A Matrix
D=zeros(3,3);
for i=1:ply_num
temp=(wQij(:,:,i).*(zlist(i+1)^3-zlist(i)^3))/3.0;
D=D+temp;
end
%%
% show result
disp('A=')
disp(A)
disp('B=')
disp(B)
disp('D=')
disp(D)
%%
% 求柔度矩阵
% A' matrix—>S1
% B' matrix—>S2
% H' matrix—>S3
% D' matrix—>S4
S1=inv(A)-(-inv(A)*B)*inv(D-B*inv(A)*B)*(B*inv(A));
S2=(-inv(A)*B)*inv(D-B*inv(A)*B);
S3=-1*inv(D-B*inv(A)*B)*B*inv(A);
S4=inv(D-B*inv(A)*B);
%%
disp('S1=')
disp(S1)
disp('S2=')
disp(S2)
disp('S3=')
disp(S3)
disp('S4=')
disp(S4)
3. TMats.m代码
function Ts=TMats(arr_angles)
% 返回3X3X3的数组,demension 3 表示第K层的T矩阵
ply_num=size(arr_angles);
ply_num=max(ply_num); % get ply's total number
Ts=[];
for i=1:ply_num
TempT=TMat(arr_angles(i));
Ts=cat(3,Ts,TempT);
end
end
function T = TMat( angle )
% TMat--input: angles of ply unit:degree -return coordinate transfer Matrix
T=zeros(3,3);
T(1,1)=cosd(angle)*cosd(angle);
T(1,2)=sind(angle)*sind(angle);
T(1,3)=2*sind(angle)*cosd(angle);
T(2,1)=sind(angle)*sind(angle);
T(2,2)=cosd(angle)*cosd(angle);
T(2,3)=-T(1,3);
T(3,1)=-sind(angle)*cosd(angle);
T(3,2)=-T(3,1);
T(3,3)=cosd(angle)^2-sind(angle)^2;
end
4. Get_zlist.m代码
function zlist = Get_zlist( ply_thickness,angles )
%返回 Z坐标的数组
%total number of plys
ply_num=size(angles);
ply_num=max(ply_num);
% total thickness
t=ply_num*ply_thickness;
%z0坐标
zlist=0;
for i=1:ply_num
zlist=cat(2,zlist,i*ply_thickness);
end
%整体下移0.5个laminate thickness
zlist=zlist-0.5*t;
end
5. Get_wQij.m代码
function wQij=Get_wQij(Q,angles)
% 输入 材料主方向的Q矩阵和铺层角度数组(1 X n)
plynum=size(angles);
plynum=max(plynum);
wQij=[];
%得到所有铺层的坐标变换矩阵
Ts=TMats(angles);
for i= 1:plynum
Ti=Ts(:,:,i);
invT=inv(Ti);
temp_wQ=invT*Q*(invT');
%追加到维度3上
wQij=cat(3,wQij,temp_wQ);
end
end
6. Get_Qij.m代码
function Qij = Get_Qij(E11,nu12,E22,G12)
%输入材料参数 E11 nu12 E22 G12 ,返回ply的折减刚度矩阵Q
% 此处显示详细说明
Q=zeros(3,3);
nu21=(E11*nu12)/(E22);
Q(1,1)=E11/(1-nu12*nu21);
Q(2,2)=E22/(1-nu12*nu21);
Q(1,2)=(E11*nu12)/(1-nu12*nu21);
Q(2,1)=Q(1,2);
Q(3,3)=G12;
Qij=Q;
end
7. 求解结果展示
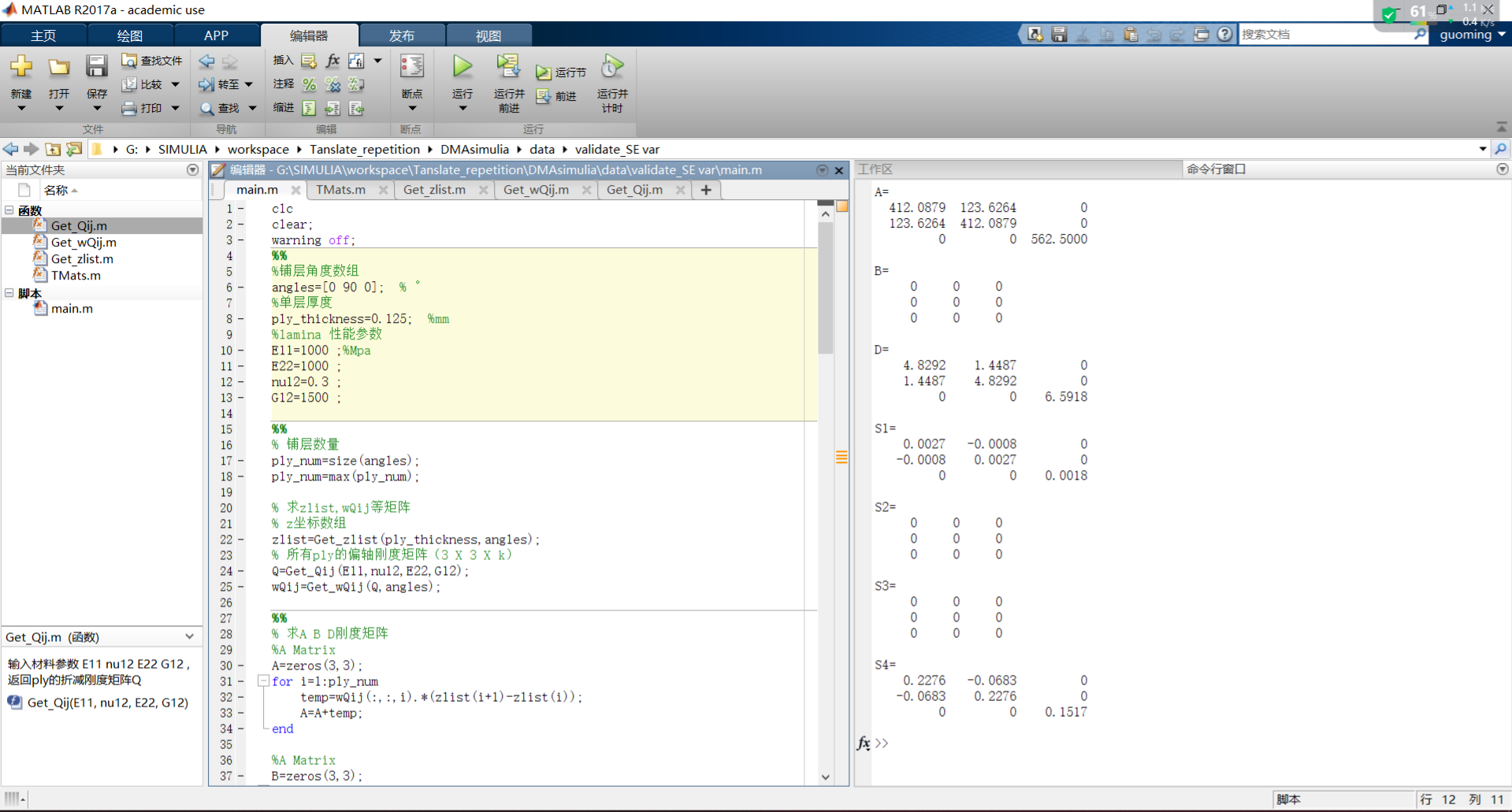
本文来自博客园,作者:FE-有限元鹰,转载请注明原文链接:https://www.cnblogs.com/aksoam/p/17065677.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号