【ABAQUS 二次开发笔记】使用keyword 、python和matlab一起处理Odb数据
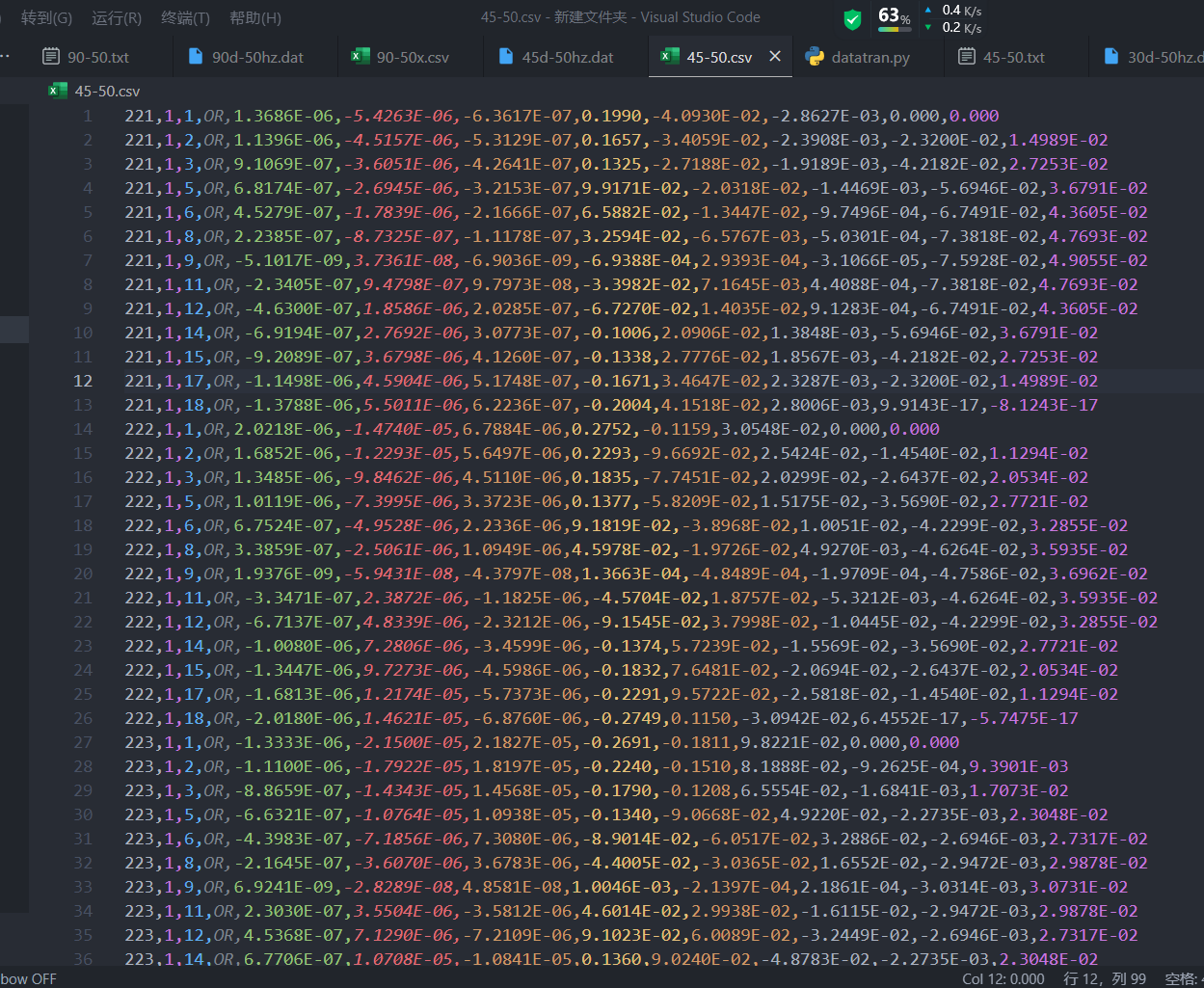
用conversion shell element (S4R单元)建模层合板,有6层ply,每个lamina(ply)有3个 integration point,共计18个integration point。我想得到集合SET-Middle-elem中所有integration point的E S TSHR13 TSHR23的output。
提取出结果后,我还需要根据剪切模量计算出13 23方向的shear strain。得到10个vars的output后,利用他们计算出整个laminate的弹性应变能(将每个单元的每个ply的弹性应变能U计算出来进行累加).计算很麻烦。
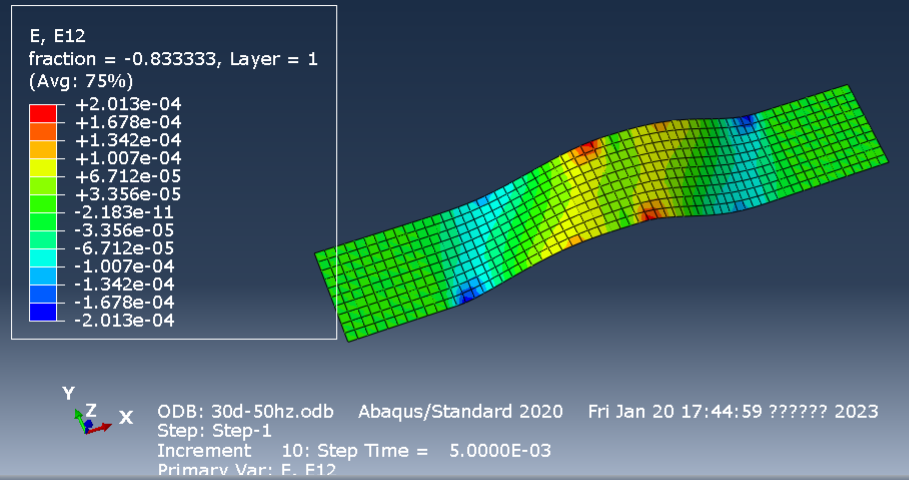
方法一:python访问odb文件
通过python 脚本访问odb文件,然后多个循环进行嵌套提取出output结果。这个办法可行,能够一下子访问到每个element的每个point.
import odbAccess
E=session.odbs['30d-50hz.odb'].steps["Step-1"].frames[10].fieldOutputs['E'].values[10]
print(E)
执行上述代码:
>>> import odbAccess
>>> E=session.odbs['30d-50hz.odb'].steps["Step-1"].frames[10].fieldOutputs['E']
>>> E.values[10]
session.openOdb(r'G:/SIMULIA/workspace/Tanslate_repetition/DMAsimulia/30d-50hz.odb').steps['Step-1'].frames[10].fieldOutputs['E'].values[10]
>>> print(E.values[10])
({
'baseElementType': 'S4R',
'conjugateData': None,
'conjugateDataDouble': 'unknown',
'data': array([0.0, -0.0, 0.0, 0.0], 'f'), 'dataDouble': 'unknown',
'elementLabel': 11,
'face': None,
'instance': 'OdbInstance object',
'integrationPoint': 1,
'inv3': 0.0,
'localCoordSystem': ((0.866025388240814, 0.5, 0.0), (-0.5, 0.866025388240814, 0.0), (0.0, 0.0, 0.999999940395355)),
'localCoordSystemDouble': 'unknown',
'magnitude': None,
'maxInPlanePrincipal': 0.0,
'maxPrincipal': 0.0,
'midPrincipal': 0.0,
'minInPlanePrincipal': 0.0,
'minPrincipal': 0.0,
'mises': 0.0,
'nodeLabel': None,
'outOfPlanePrincipal': 0.0,
'position': INTEGRATION_POINT,
'precision': SINGLE_PRECISION,
'press': -0.0,
'sectionPoint': 'SectionPoint object',
'tresca': 0.0,
'type': TENSOR_3D_PLANAR
}
)
>>> len(E.values)
10800
可以看出,在用odb的话就会循环非常多次才能算完,并且不容易定位到单个element。我感觉用python的话会code会非常混乱,逻辑不容易理清,因此放弃。
方法二:edit keywords 输出到dat文件,然后用MATLAB编程计算
通过关键字*EL PRINT可以将多个变量在指定积分点上的结果进行输出。这样输出有个好处就是,输出的结果ABAQUS会整理为 类似 table的样式。
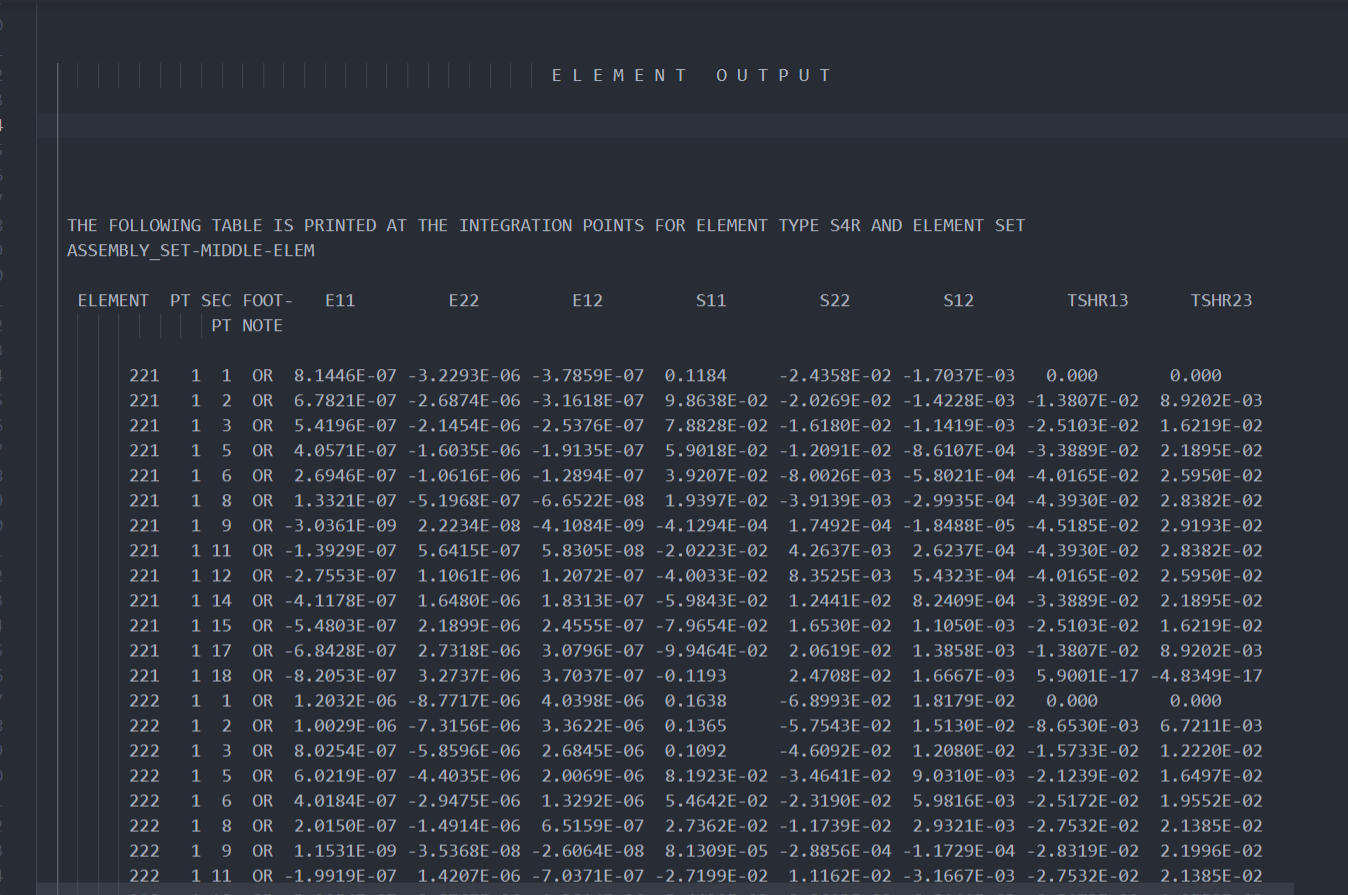
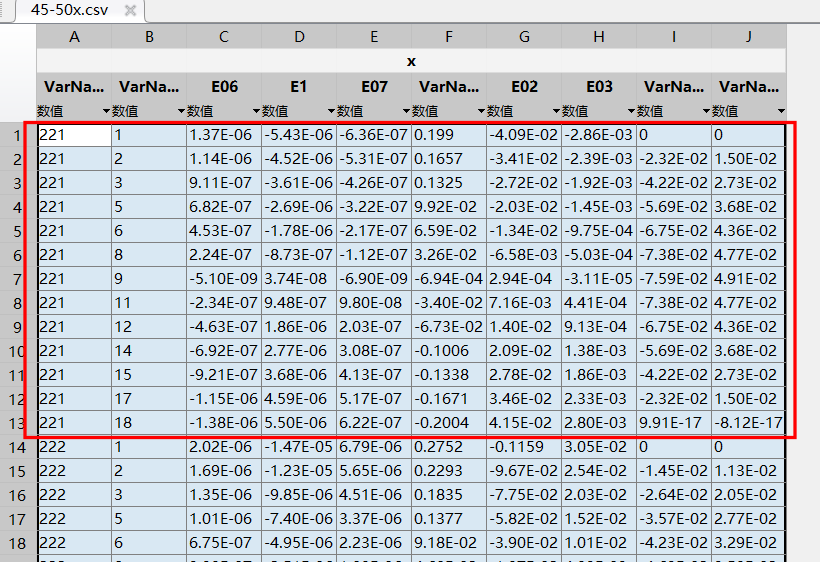
这样的格式我可以用python进行处理,写入CSV文件。
但是使用*EL PRINT有一个问题比较麻烦:*EL PRINT关键字语句的 first data line 一次最多16个section integration point ,多于16个integration point 则需要重复使用*EL PRINT来输出结果。而我有18个integration point 如果分两次输出的话。那输出的就是两个 table .得到结果我还需要整合成一个matrix。不方便。
但是幸好,composite laminate 的每个ply之间是应力应变满足连续性条件。我可以不输出几个重合的integration point:
Aindex=[3 5 7 9 11]
后续需要在matlab中写一个function,恢复这五个integration point 的output。
function B = expanMat(A,Aindex)
%将13个积分点数据展开为18个积分点的矩阵
B=[];
sizeAindex=size(Aindex);
if isempty(Aindex)
B=A;
disp('A矩阵未改变')
else
%如果only移动一行就不循环了
if sizeAindex(1)+sizeAindex(2)==2
B=cat(1,A(1:Aindex(1),:),A(Aindex(1),:),A(Aindex(1)+1:end,:));
else
%把index向量升序排序
Aindex=sort(Aindex);
%得到A的行数
rows=size(A);
rows=rows(1);
%loop A matrix
for i=1:rows
temp=A(i,:);
% if the row operated is the member of Aindex(a array containts indexs of all rows needed to copy)
if ismember(i,Aindex)
B=cat(1,B,[temp;temp]);
else
B=cat(1,B,temp);
end
end
end
end
end
最后:
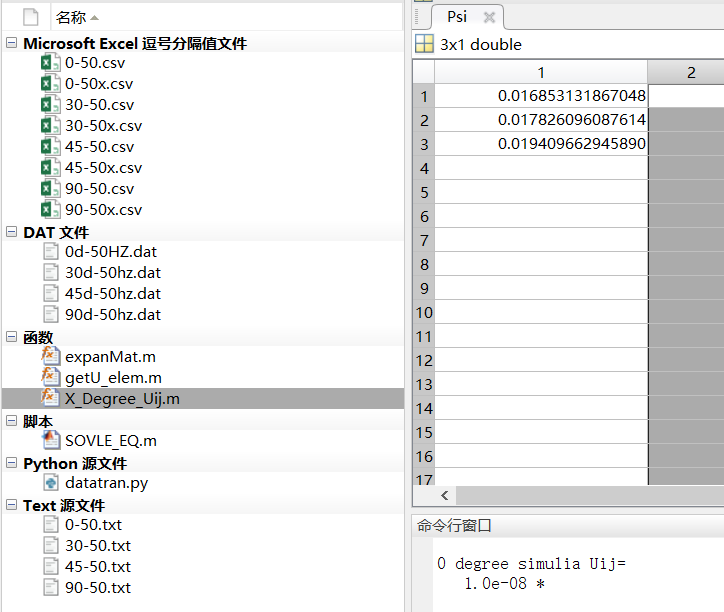
算出来的最小二乘结果,感觉误差比较大。
本文来自博客园,作者:FE-有限元鹰,转载请注明原文链接:https://www.cnblogs.com/aksoam/p/17063398.html