Abaqus-Steady-State-Dynamic-Analysis的求解原理

0. 总括

基于模态的谐响应分析，可以通过扫频的方式求解频率范围内结构的线性稳态响应情况。阻尼是和频率相关的，但模态叠加法只需要知道n个模态阻尼即可推广到其他频率范围（原因详见文内公式）。

1. 谐响应分析的目的

用来求解结构在连续谐波激励下的线性响应.求解稳态动力学响应有三种方法：subspace,direct,modal。base modal的方法是利用前一个分析步提取出来的一系列模态特征计算稳态解。

2. ABAQUS的求解原理

2.1 特征值提取

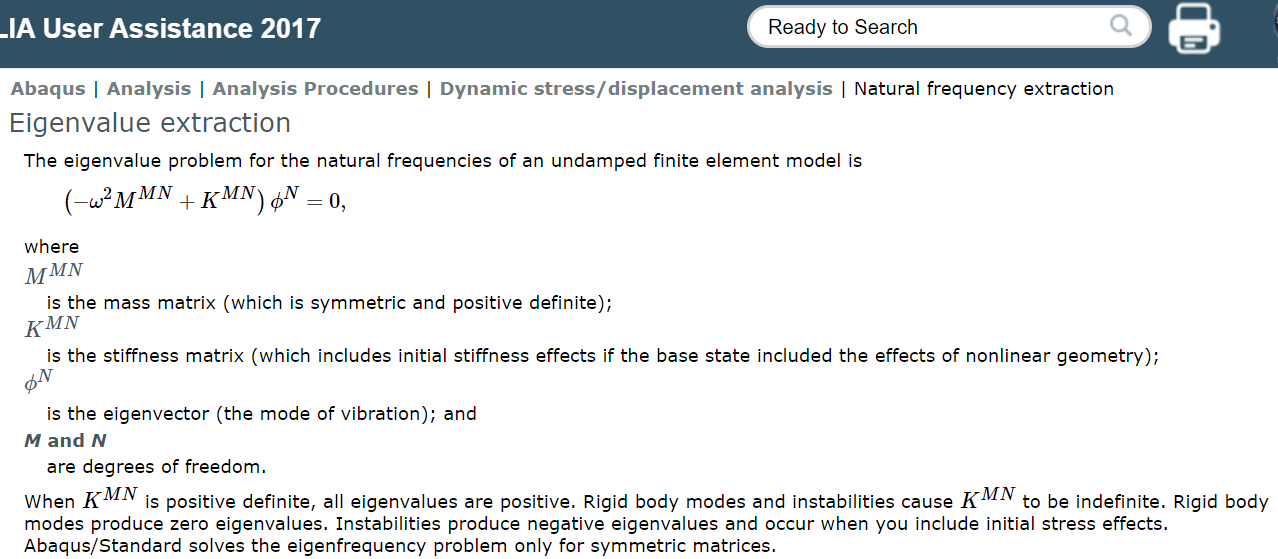
对于一个具有N个自由度的多自由度系统，可用N个独立的广义坐标描述系统的运动状态：

\[a^{N\times1}=\{a_1,a_2,a_3,...,a_N\}^{T} \]

对于N自由度的系统，一定可以找到N个固有频率\(w_{\alpha}\)以及相对应的振型\(\phi_{\alpha}^{N\times1}\) 【\(\alpha=1...n，n是提取的模态的数目\)】 。\(\phi^{N}\)左边的矩阵是\(M\times N\)的,等号右边是0，所以\(\phi^{N}\)是\(N\times 1\)的。

所谓振型按我的理解就是共振时，结构的一个形状。用数学方式表示就是一个特定的解向量\(\phi_{\alpha}^{N}\)

将\(\phi_{\alpha}^{N\times 1}\)组装成 Nxn 矩阵\(\Phi\)，其中每一列都包含一个特征模态。

2.2 模态叠加

有阻尼的结构动力学方程：

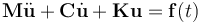
模态叠加用矩阵形式写为

\[u^{N\times1}=\Phi^{N\times n} q^{n\times 1} \]

列矢量\(q\)——模态自由度（待求）
在运动方程中插入模态叠加表达式,代入动力学方程：

\[M\Phi \ddot{q}+C\Phi \dot{q}+K\Phi q=f(t)^{N \times1} \]

左乘\(\Phi^{T}\)后得到：

\[\Phi^{T}M\Phi \ddot{q}+\Phi^{T}C\Phi \dot{q}+\Phi^{T}K\Phi q=\Phi^{T}f(t)^{N\times 1} \]

此时，原方程组现已从求解 N 个变量简化为 n 个变量，右侧$\Phi^{T}f(t) $为模态载荷，是外载荷在每个特征模态上的投影。

\[\Phi^{N\times n}=[\phi_1,\phi_2,\phi_3,...,\phi_n] \]

\[\Phi^{T}=[\phi_1^T,\phi_2^T,\phi_3^T,...,\phi_n^T] \]

\[f(t)^{N\times 1}= \begin{bmatrix} f(t)_1 \\ f(t)_2 \\ f(t)_3 \\ ....\\ f(t)_N \end{bmatrix} \]

\[\Phi^{T}f(t)^{N\times 1} = \begin{bmatrix} \phi_1f(t)_1\\ \phi_2f(t)_2\\ \phi_3f(t)_3\\ ...\\ \phi_nf(t)_n\\ \end{bmatrix} \]

上式经过一系列变换后，可以得到投影到mode \(\alpha\)上的方程\((1)\)：

\[\ddot{q}_{\alpha}+c_{\alpha}\dot{q}_{\alpha}+\omega_{\alpha}^2q_{\alpha}=\frac{1}{m_{\alpha}}(f_{1\alpha}+if_{2\alpha})exp(i\Omega t) \]

其中：

\(q_{\alpha}\):$mode \ \alpha $下的广义坐标幅值

\(c_{\alpha}\):\(与mode \ \alpha\)有关的阻尼(模态阻尼)

\(\omega_{\alpha}\):\(mode \ \alpha\)下的无阻尼固有频率

\(m_{\alpha}\)：广义质量,\(m_{\alpha}=\Phi_{\alpha}^{N}M^{N\times M}\Phi_{\alpha}^{M} \ \ (no \ sum\ over\ \alpha)\)

\((f_{1\alpha}+if_{2\alpha})e^{i\Omega t}\):是和$mode\ \alpha $有关的激励

2.2.1 激励项

激励被\(frequency (\Omega)\),节点等效力实、虚部\((F_{1}^{N},F_{2}^N)\)定义。投影到\(mode\ \alpha\)上：

\[f_{1\alpha}+if_{2\alpha}=\phi_{\alpha}^N(F_{1}^{N}+iF_{2}^N)\\ N——模型自由度数 \]

载荷向量是根据其实部\(F_{1}^{N}\)和虚部\(F_{2}^{N}\)编写的，这是Abaqus/Standard 中定义载荷的方式.如果偶用幅值\(F_{0}^N\)和相位\(\Phi\)表示，则有

\[F^N=F_1^N+iF_2^N=F_{0}^{N}exp[i(\Omega t+\Phi)] \]

其中：

\(F_1^N=F_0^Ncos(\Phi) \ \ \ \\ F_2^N=F_0^Nsin(\Phi)\)

2.2.2 阻尼项

• 直接模态阻尼：\(c_\alpha=2\zeta_{\alpha}\omega_{\alpha}\)
  其中:\(\zeta_{\alpha}是mode \ \alpha下的临界阻尼分(模态阻尼比)\)
• Structure Damp：提供了与模态振幅成比例的阻尼力。
  \(c_{\alpha}\dot{q}_{\alpha}=i s_{\alpha}\omega_{\alpha}^2 q_{\alpha}\)
  其中:\(s_{\alpha}是mode \ \alpha 的结构阻尼系数(模态损耗因子)\)
• 瑞利阻尼：定义为\(c_{\alpha}=\beta_{\alpha}+\gamma_{\alpha}\omega_{\alpha}^2\)
  其中，\(\beta_{\alpha}、\gamma_{\alpha}\)是瑞利阻尼系数，具体求法见Document.
  瑞利阻尼系数可以用来再现：

\[\zeta_{\alpha}=\frac{\beta_{\alpha}}{2\omega_{\alpha}}+\frac{\gamma_{\alpha}\omega_{\alpha}}{2} \]

将阻尼项代入方程(1):

\[\ddot{q}_{\alpha}+2\zeta_{\alpha}\omega_{\alpha}\dot{q}_{\alpha}+(\beta_{\alpha}+\gamma_{\alpha}\omega_{\alpha}^2)\dot{q}_{\alpha}+i s_{\alpha}\omega_{\alpha}^2 \dot{q}_{\alpha}+\omega_{\alpha}^2q_{\alpha}=\frac{1}{m_{\alpha}}(f_{1\alpha}+if_{2\alpha})exp(i\Omega t) \]

方程的解为：

\[\dot{q}_{\alpha}=H_{0\alpha}*f_{0 \alpha}* exp(i(\Omega t+\Phi_{\alpha})) \]

方程中有三个阻尼项对应于，ABAQUS/CAE中只定义一个，其他的就是0.

其中：

\(f_{0\alpha}=\sqrt{f_{1\alpha}^2+f_{2\alpha}^2}是投影载荷矢量的振幅\)

\(H_{0\alpha}(\Omega)是mode\ \alpha下系统复传递函数的振幅\)

\[Re(H_{0\alpha}f_{0\alpha})=\frac{1}{m_{\alpha}} (\frac{f_{1\alpha}(\omega_{\alpha}^2-\Omega^2)}{(\omega_{\alpha}^2-\Omega^2)^2+(\eta_{\alpha}\Omega)^2}+\frac{f_{2\alpha}\eta_{\alpha}\Omega}{(\omega_{\alpha}^2-\Omega^2)^2+(\eta_{\alpha}\Omega)^2}) \]

\[Im(H_{0\alpha}f_{0\alpha})=\frac{1}{m_{\alpha}} (-\frac{f_{1\alpha}\eta_{\alpha}\Omega}{(\omega_{\alpha}^2-\Omega^2)^2+(\eta_{\alpha}\Omega)^2}+\frac{f_{2\alpha}(\omega_{\alpha}^2-\Omega^2)}{(\omega_{\alpha}^2-\Omega^2)^2+(\eta_{\alpha}\Omega)^2}) \]

其中：

\[\eta_{\alpha}=2\zeta_{\alpha}\omega_{\alpha}+\beta_{\alpha}+\gamma_{\alpha}\omega_{\alpha}^2+\frac{s_{\alpha}\omega_{\alpha}^2}{\Omega} \]

响应的幅值为：

\[H_{0\alpha}f_{0\alpha}=\sqrt{Re(H_{\alpha})^2+Im(H_{\alpha})^2}=\frac{1}{m_{\alpha}}\frac{1}{\sqrt{(\omega_{\alpha}^2-\Omega^2)^2+(\eta_{\alpha}\Omega)^2}}f_{0\alpha} \]

响应的相位：

\[\Psi_{\alpha}=acrtan(Im(H_{\alpha})/Re(H_{\alpha})) \]

如果谐波激励以base motion的形式施加，那么模态载荷如下：

\[f_{1\alpha}=-\frac{1}{m\alpha} \phi_{\alpha}^{N}M^{NM}\hat{e}_j^{M}a_{1j}exp(i\Omega t)\\ f_{2\alpha}=-\frac{1}{m\alpha} \phi_{\alpha}^{N}M^{NM}\hat{e}_j^{M}a_{2j}exp(i\Omega t) \]

其中，\(M^{NM}\)是结构的质量矩阵，\(\hat{e}_{j}^{M}是一个vector(在任何接地节点上的基础加速度，方向上具有单位幅值，否则为零)\)

\(a_{1j}、a_{2j}\)是base acceleration的实部和虚部。如果施加的是velocity(或者displacement) 则\(a_1=-\Omega v_1\ \ \ a_2=-\Omega v_2\)或(\(a_1=-\Omega^2 u_1 \ \ \ a_2=-\Omega^2 u_2\))。

综上所述，根据模态叠加的基本假设：位移写为特征模态的线性组合。
方程(1)的解\(q_{\alpha}\)为

\[q_{\alpha}=H_{0\alpha}f_{0\alpha}exp[i(\Omega t+\Phi_{\alpha})] \]

这是外加激励频率为\(\Omega\)，在\(mode\ \alpha\)下的解，经过模态叠加(如下)后可以得到位移响应(式2)：

\[u^N=\sum_{\alpha}^{n}{\phi_{\alpha}^N q_{\alpha}} \]

其中：

\(q_{\alpha}:每个模态的幅值求解结果\)

\(\phi_{\alpha}^N:mode\ \alpha的特征向量向量（N \times1）即振型向量\)

稳态响应以通过用户指定频率范围的频率扫描形式给出。依次扫描频率点，就可以求出结构的频域响应。

参考资料

• COMSOL仿真百科
• ABAQUS Theory-稳态动力学分析
• MOOC-振动理论
• 《结构动力学 第二版》作者：R。克拉夫等