阻尼、模态应变能法与FRP的关系

阻尼的概念

• 系统损耗振动能或声能的能力称为阻尼

• 阻尼越大,输人系统的能量便能在较短时间内损耗完毕.系统从受激振动到重新静止所经历的时间就越短;

• 阻尼也可理解为系统受激后迅速恢复到受激前状态的一种能力

阻尼的基本原理就是损耗能量，所以阻尼也可以看成是一种内耗。把输入的能量转化为其他的能量。其物理意义是：系统损耗的能量和输入的能量的比值，是一个无量纲参量。^[1]

对于完全弹性体，根据弹性理论的广义胡克定律，材料在弹性变形过程中应力应变满足以下关系：

\[\sigma=E \epsilon或者\tau=G\gamma \]

上述公式有三个条件：

1. \(\sigma-\epsilon 是线性响应关系，即线性\)
2. \(\sigma-\epsilon 相位差为0，即瞬时性\)
3. \(应变是应力的单值函数，即唯一性\)

而实际情况，并不会完全满足三个条件——表现出非理想弹性，产生阻尼。非理想弹性有滞弹性和粘弹性（在玻璃转变点附近的玻璃体及高温下的多晶体材料，其弹性模量不再为常数，而是表现为与时间有关的弹性行为，即滞弹性）。根据滞弹性是否是线性的分为非线性滞弹性和线性滞弹性，所以阻尼可分为线性滞弹性阻尼、非线性滞弹性阻尼、粘弹性阻尼。

• 滞弹性：材料有应变落后于应力的现象，这种现象称为滞弹性，它表征材料的形变在应力移去后能够恢复但不是立即恢复的能力。
• 粘弹性：材料不仅具有弹性，而且具有摩擦。当应力被移除后，一部分功被用于摩擦效应而被转化成热能

表征阻尼的参量

常见参量如下：^[2][3]

• 比阻尼
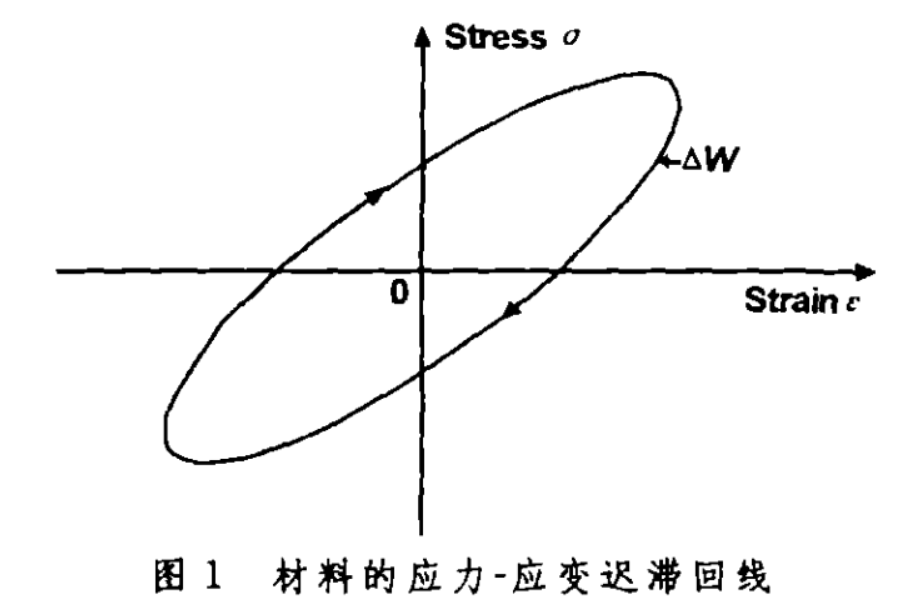
  给试样施加一个循环应力\(\sigma\) ，由于应变\(\epsilon\) 落后于应力\(\sigma\) 从而出现应力-应变回线（如下图），回线的面积就代表了振动一周时单位体积的试样消耗的能量，因此比阻尼能力定义为：

\[\phi=\frac{\Delta U}{U} \]

式中，\(\phi\)为比阻尼能力，$ \Delta U \(是振动一周时单位体积的试样消耗的能量,<mark>正比于回线的面积</mark>。\)U$ 是单位体积试样振动过程中存储的最大应变能（外界提供的应变能）

文献[2]中说法是弹性能，和应变能应该是一个东西，\(U=0.5\sigma\epsilon\)（一维线弹性材料），材料力学定义线弹性范围内弹性变形能即应变能

• 相位差的正切值
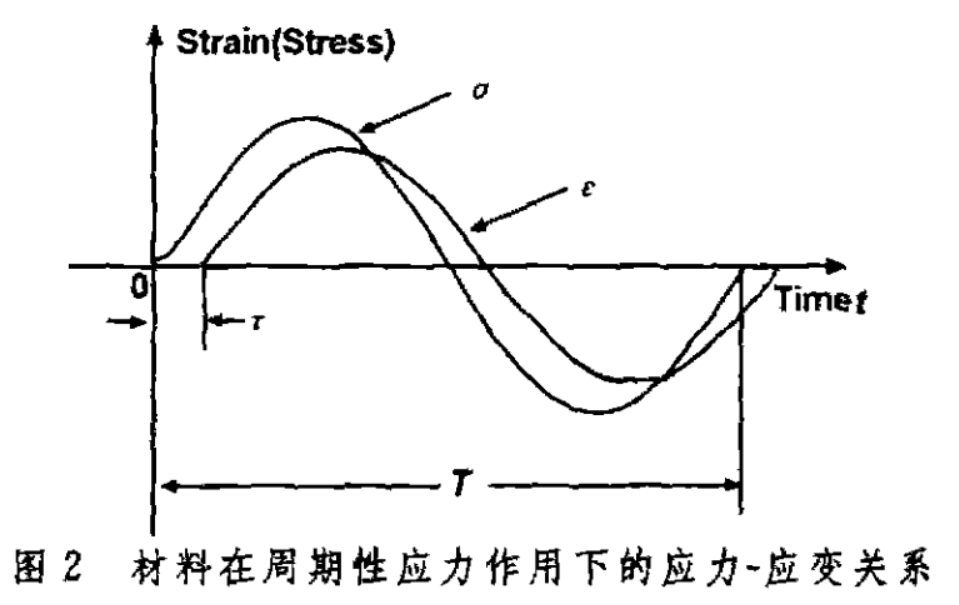
  材料在周期应力作用下，受激产生周期振动，之后继续施加应力，试样就会受迫振动。振动达稳态后，试样将按照周期应力的频率振动，应变的相位落后应力相位，相位差为\(\Phi\)如下图。\(\Phi\)可表示为：

\[\Phi=\frac{t}{T} \times 2\pi \]

式中，\(t\)是\(\epsilon\)落后\(\sigma\)的时间，\(T\)是外加应力的周期，材料阻尼能力越高，那么相位差角就越大，正切值\(tan(\Phi)\)越大。

相位差角适合内耗大的情况，内耗小则比较难测量应力和应变曲线的时间差值。

• 对数衰减率 \(\delta\)
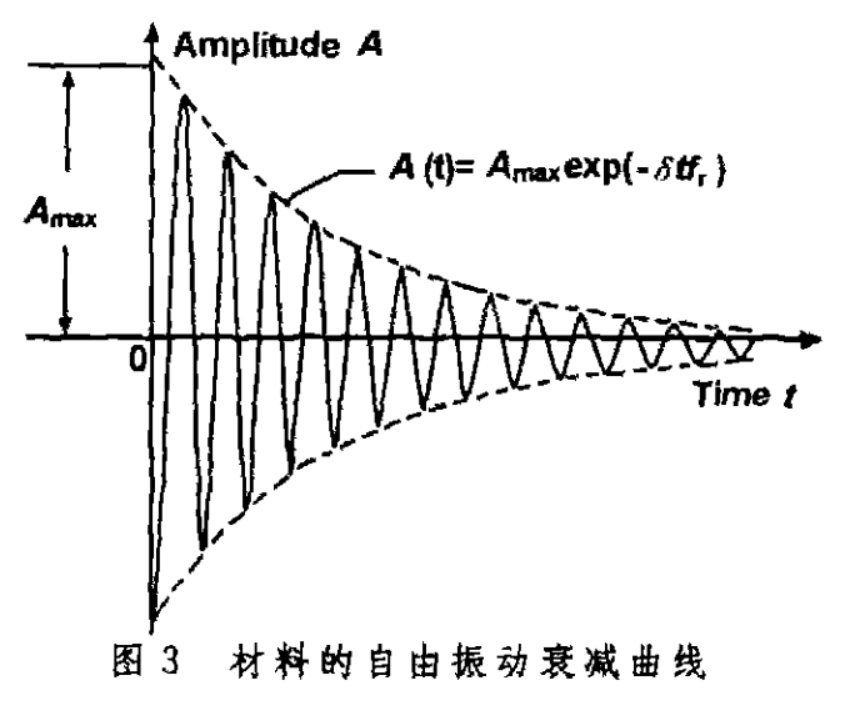
  材料自由振动过程中，振动的幅度会之间衰减，衰减的越快那就代表阻尼性能越高。定义：

\[\delta=\frac{1}{n} ln(\frac{A_i}{A_{i+n}}) \]

其中，n=1,2,3,...为振动循环次数。\(A_i\)是第\(i\)次振动的振幅，\(A_{i+n}\)是次的振动振幅，对数衰减率表征振幅衰减的程度，越大则阻尼性能越好。

属于共阵法的一种，适合测试声频阻尼（不懂）

• 品质因子倒数
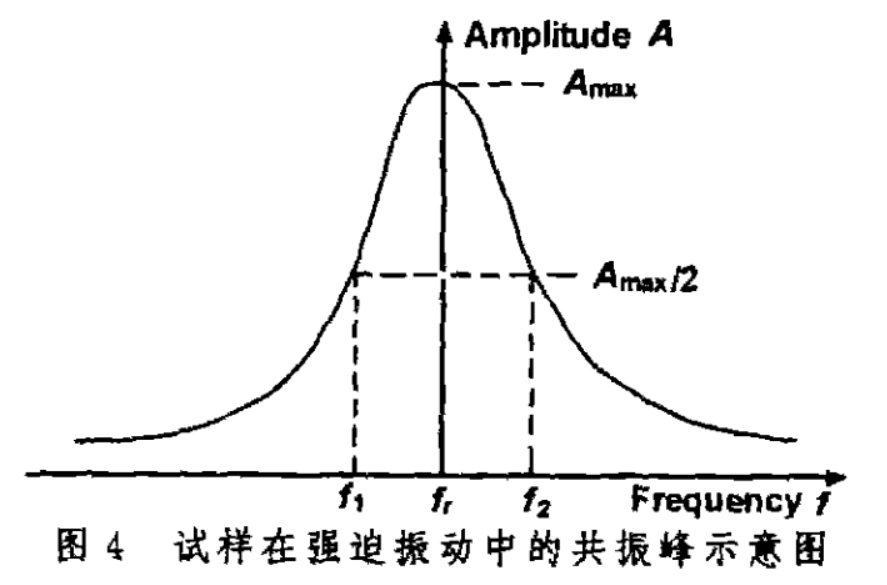
  用不同频率外力激发试样，如果外力频率=试样共振频率那么试样振动的振幅最大。相同条件下，材料阻尼性能越高，那么共振振幅越小，共振峰越宽。所以可以用振峰的尖锐程度表示材料阻尼能力的大小，定义：

\[Q^{-1}=\frac{|\Delta f|}{\sqrt{3} f_r} \]

式中,
\(Q^{-1}\)：品质因子倒数;\(\Delta f\) ：共振振幅一半处的频率差值\(f_2-f_1\)，\(f_r\):共振频率
材料阻尼性能越高，共振峰越宽，测量越准。

适合测试声频阻尼

• 其他参量
  • 损耗因子\(\eta\)
  • 阻尼比\(\xi\)
  • 损失模量和存储模量之比\(\frac{M_2}{M_1}\)

当阻尼比较小的时候，如\(tan(\Phi)<0.1\)。

\[tan(\Phi)=\Phi=\eta=Q^{-1}=\phi/2\pi=\delta/\pi \]

阻尼比较大的时候，如比阻尼\(\phi>0.4\)。常用比阻尼表示阻尼性能

\[\phi=1-exp(-2\delta) \]

分类

从设置阻尼的方法来看：

1. 系统阻尼：系统中设置专用阻尼减振器,如减振弹簧、冲击阻尼器
2. 结构阻尼:系统的某一振动结构上附加材料或形成附加结构,增加系统自身的阻尼能力
3. 材料阻尼：依靠材料本身所具有的高阻尼特性达到减振降噪

阻尼材料的分类：

1. 粘弹性阻尼材料
2. 高阻尼合金材料
3. 复合阻尼材料
   1. 聚合物基阻尼复合材料
   2. 金属基阻尼复合材料
4. 智能型阻尼材料
   1. 压电阻尼材料
   2. 电流变流体阻尼材料

评价阻尼性能的实验方法：

• 动态扭摆法TBA
• 受迫共振法
• 受迫振动非共振法
  • 动态粘弹实验DMA
  • 差示扫描量热分析法 ＤＳＣ

纤维增强复合材料的阻尼机理

纤维增强复材的阻尼机理和合金不同。主要表现在：^[4]

• matrix和fibre的粘弹性阻尼
• fibre/matrix间的中间相阻尼
• 材料中微结构损伤（脱胶区、集体断裂处、断裂纤维）的滑动摩擦阻尼
• 局部应力集中的非线性粘弹性阻尼
• 周期热流动产生的热弹性阻尼。

应用较广的材料有限阻尼性能预测方法：

• 弹性-黏弹性对应原理
• 最大应变能法

最大应变能法（max strain energy method-SEM）

——任何含有线性粘弹性元的系统的损耗因子都可以表示为每个元的损耗因子与所存储的应变能的百分比的乘积之和，SEM方法应用在纤维增强复合材料时，认为复合材料时一个系统，没有一个单层板就是一个元。^[4:1]

在给定频率和振幅下执行稳态振动的结构的损耗因子定义为：

\[\eta = \frac{\Delta U}{2\pi U} \]

\(\Delta U —表示每个循环耗散的能量（或必须提供给系统以保持稳态条件的能量）\)
\(U —存储的应变能\)
这是一个反映材料本身阻尼性能的量

出自《Loss Factors of Viscoelastic Systems in Terms of Energy Concepts》

假设复合材料如下图

该系统的损耗因子\(\eta_{sys}\)，根据最大应变能法可知：

\[\eta_{system}=\sum_{i=1}^{n}{\eta_i*\omega_i} \]

\(\omega_i :每一个layer所存储的应变能的百分比，即\)

\[\omega_i=\frac{U_i}{(U_1+U_2+U_3+...+U_{last})} \]

\(\eta_i:每个元对应的损耗因子\)

上式展开后：

\[\eta_{system}=\frac{\sum_{i=1}^{n}\eta_i U_i}{U_1+U_2+U_3+...+U_{last}} \]

当材料被制作成为构件，在某个状态下复杂受力使得不同部位的材料应力分布并不均匀时，将其离散为若干的单元，分别计算每个单元的弹性应变能并假定这个单元内的应力分布式均匀的，从而就可以利用材料损耗因子的定义计算得到这个单元在一个周期内的耗能。将所有单元在一个周期内的耗能总和与所有单元的弹性能总和，用材料损耗因子的定义作类似的运算，就可以得到构件或结构层面的损耗因子，也就是上面的 \(\eta_{system}\)

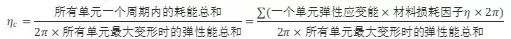
构件层面的损耗因子描述的是在一个周期（以特定的振动形式）的耗能与构件弹性能的对应关系。这意味着，如果已知构件的特定模态形式下的弹性能就可以评价在这个模态下的耗能(阻尼)。

---

1. 新型阻尼材料的研究进展_顾健. ↩︎

2. 材料阻尼及阻尼材料的研究进展_张忠明. ↩︎

3. 材料阻尼及阻尼合金的研究现状_李沛勇. ↩︎

4. 纤维增强复合材料结构阻尼研究进展_任勇生. ↩︎ ↩︎