扩大
缩小

BZOJ3944 Sum

3944: Sum

Time Limit: 10 Sec  Memory Limit: 128 MB

Description

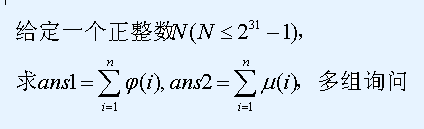
Input

一共T+1行
第1行为数据组数T(T<=10)
第2~T+1行每行一个非负整数N，代表一组询问

Output

一共T行，每行两个用空格分隔的数ans1,ans2

Sample Input

6
1
2
8
13
30
2333

Sample Output

1 1
2 0
22 -2
58 -3
278 -3
1655470 2
杜教筛入门
其实就是通过
\[ \sum\limits_{i=1}^n\sum\limits_{d|i}\mu(d) = 1 \]
\[ \sum\limits_{i=1}^n\sum\limits_{j=1}^{\left\lfloor\frac{n}{i}\right\rfloor}\mu(j) = 1 \]
\[ \sum\limits_{i=1}^n\mu(i) = 1-\sum\limits_{i=2}^n\sum\limits_{j=1}^{\left\lfloor\frac{n}{i}\right\rfloor}\mu(j) \]
然后预处理前\( n ^ {\frac{2}{3}} \)个函数值，询问时递归处理。
 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 template <class _T> inline void read(_T &_x) {
 4     int _t; bool flag = false;
 5     while ((_t = getchar()) != '-' && (_t < '0' || _t > '9')) ;
 6     if (_t == '-') _t = getchar(), flag = true; _x = _t - '0';
 7     while ((_t = getchar()) >= '0' && _t <= '9') _x = _x * 10 + _t - '0';
 8     if (flag) _x = -_x;
 9 }
10 typedef long long LL;
11 const int maxn = 5000000;
12 LL phi[maxn], mu[maxn];
13 int prime[maxn / 10], pcnt;
14 bool vis[maxn];
15 inline void init() {
16     phi[0] = mu[0] = 0;
17     phi[1] = mu[1] = 1;
18     for (int i = 2; i < maxn; ++i) {
19         if (!vis[i]) {
20             prime[++pcnt] = i;
21             mu[i] = -1, phi[i] = i - 1;
22         }
23         for (LL j = 1, tmp; j <= pcnt && (tmp = prime[j] * i) < maxn; ++j) {
24             vis[tmp] = true;
25             if (i % prime[j] == 0) {
26                 phi[tmp] = phi[i] * prime[j];
27                 mu[tmp] = 0;
28                 break;
29             }
30             phi[tmp] = phi[i] * (prime[j] - 1);
31             mu[tmp] = -mu[i];
32         }
33     }
34     for (int i = 2; i < maxn; ++i) phi[i] += phi[i - 1], mu[i] += mu[i - 1];
35 }
36 map<LL, LL> Mphi, Mmu;
37 LL Phi(LL n) {
38     if (n < maxn) return phi[n];
39     if (Mphi.find(n) != Mphi.end()) return Mphi[n];
40     LL ret = ((LL)n * (n + 1)) >> 1;
41     for (LL i = 2, j, t; i <= n; i = j + 1) {
42         t = n / i, j = n / t;
43         ret -= (j - i + 1) * Phi(t);
44     }
45     Mphi[n] = ret;
46     return ret;
47 }
48 LL Mu(LL n) {
49     if (n < maxn) return mu[n];
50     if (Mmu.find(n) != Mmu.end()) return Mmu[n];
51     LL ret = 1;
52     for (LL i = 2, j, t; i <= n; i = j + 1) {
53         t = n / i, j = n / t;
54         ret -= (j - i + 1) * Mu(t);
55     }
56     Mmu[n] = ret;
57     return ret;
58 }
59 int main() {
60     //freopen();
61     //freopen();
62     init();
63     LL T, N; read(T);
64     while (T--) {
65         read(N);
66         printf("%lld %lld\n", Phi(N), Mu(N));
67     }
68     return 0;
69 }
View Code

 

posted @ 2017-05-09 16:38  HPLV  阅读(138)  评论(0)  编辑  收藏  举报