K-D Tree

K-D Tree

阅读本文的一些注意事项：

• 演示代码使用结构体封装每个节点
• 如果没特别说明两个子树或者左/右子树，子树指这个节点和它的所有子节点
• 由于 K-D Tree 的写法很多，所以这里没有放模板，模板题可以上OI-Wiki查看

---

K-D Tree(k-Dimension Tree) 是一种可以 高效处理k维空间信息 的暴力数据结构。

在算法竞赛的题目中，一般有K=2，所以本文默认K=2（其它情况无较大区别）。

给出一个例子方便理解

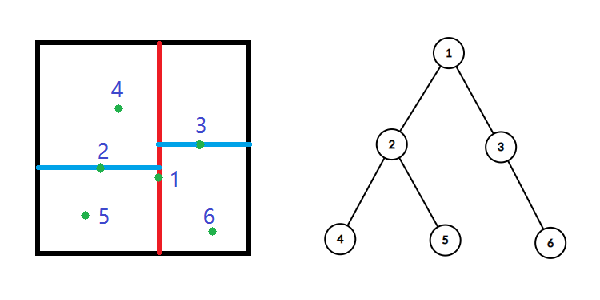
需要维护的信息：

• 两个儿子的编号
• 当前节点的坐标
• 子树所有节点每个维度坐标的最大最小值，即这个节点所表示的超长方体的边界
• 可能需要维护节点大小（判断是否需要重构时需要用到）
• 其它需要维护的东西

建树

K-D Tree 具有二叉搜索树的形态，树上的每个结点都对应一个点，每个节点的子树中的节点都在一个K维超长方体中，且每一层的任意两个不同节点的超长方体除边界外不交。

假设我们已经知道了一些点，用这些点建一棵 K-D Tree 的步骤如下：

• 选择一个维度，选出一个点，将这个点放在当前节点处
• 以这个点当前维度的坐标为基准，将当前维度坐标小于等于这个基准的点（不包含当前选择的点）和其余的点分开，分别置于两个子树。
• 递归处理并上传信息。

维度的选择

为了保证后面查询的复杂度，在选择维度的时候，最好选择分布较散的维度（具体为什么我也不知道），即方差较大的维度，或者你也可以轮流选择维度。

节点的选择

为了保证在建树的时候使树尽量平衡，在选择点的时候我们可以选择该维度上的中位数，这样在每次分割的时候左右两个子树大小的差不超过1。

对于求中位数，尽量使用O(n)的方法，具体实现方式不在这里讲述，这里仅提供一个stl函数，被包含在库algorithm中：nth_element(a + l, a + mid, a + r + 1, cmp)，可以将序列部分排序，排序后保证a[l, mid)中的所有值都小于a[mid]，a(mid, r]中的所有值都大于a[mid]（mid在中间，不要放在后面，否则会和暴力差不多）。

大致模板

这里放一个模板便于理解

pair<int, int> a[100001];
bool cmp1(pair<int, int> a, pair<int, int> b) {
	return a.first == b.first ? a.second < b.second : a.first < b.first;
}
bool cmp2(pair<int, int> a, pair<int, int> b) {
	return a.second == b.second ? a.first < b.first : a.second < b.second;
}
int build(int l, int r) {
	int p = ++ cnt;
	int avx = 0, avy = 0, sx = 0, sy = 0;
	for(int i = l; i <= r; i ++) avx += a[i].first, avy += a[i].second;
	avx /= (r - l + 1), avy /= (r - l + 1);
	for(int i = l; i <= r; i ++)
		sx += (a[i].first - avx) * (a[i].first - avx), sy += (a[i].second - avy) * (a[i].second - avy);
	int mid = (l + r) >> 1;
	if(sx > sy) nth_element(a + l, a + mid, a + r + 1, cmp1);
	else nth_element(a + l, a + mid, a + r + 1, cmp2);
	if(l < mid) t[p].son[0] = build(l, mid - 1);
	if(r > mid) t[p].son[1] = build(mid + 1, r);
	t[p].x = a[mid].first, t[p].y = a[mid].second;
	push_up(p);
	return p;
}

插入和删除

插入

如果需要支持插入，我们就需要对每个节点额外维护在建树的时候选择的维度，然后插入时比较这个维度确定插入哪个子树。

插入一些节点后，树的平衡性无法保证（虽然不故意卡还是勉强能够用），这时候我们就要用类似替罪羊树的重构思想：如果某个节点的左子树或者右子树的大小占比超过某一个值，就直接重构这个节点的子树

删除

对于删除操作，我们只需要在被删除的节点处打一个标记并且删除这个节点在所有祖先节点处的贡献（惰性删除），在重构的时候再将这些节点删除。

在查询最近点对的时候，已经被删除的节点不能计入大小，在删除节点后要检查是否需要进行重构，如果是查询某个超长方体，则不一定要这样。

邻域查询

邻域查询即查询距离某个高维空间点最近（远）的点之类的问题，K-D Tree 处理这些问题的时间复杂度是不确定的，最坏能够达到O(n)，使用的时候需要注意一下。

首先是最暴力的方法，直接枚举整棵树，求答案。

上面这种方法可以使用最优化剪枝，如果当前超长方体中的所有点（指空间意义下的点，不一定是某个节点）都不优，那么可以直接忽略掉这棵子树。

以最近点，二维空间为例，如果当前子树的矩形的四个角（当然我们不一定要枚举四个角）到指定点的距离都超过的当前的答案，那么这个子树中的所有点到指定点的距离一定都超过了答案，所以我们可以不需要计算这棵子树。

此外，我们还可以使用启发式搜索的方法，即如果某个节点的两棵子树都可能存在答案，那么我们优先递归答案下界更小的那棵子树，答案下界即为超长方体中的所有点（指空间意义下的点）到指定点的最小距离。

放一个大致模板便于理解

int g(int p, int x, int y) {
	int ret = 0;
	if(t[p].lx > x) ret += t[p].lx - x;
	if(t[p].rx < x) ret += x - t[p].rx;
	if(t[p].ly > y) ret += t[p].ly - y;
	if(t[p].ry < y) ret += y - t[p].ry;
	return ret;
}
int ans = 2e9;
void query(int p, int x, int y) {
	ans = min(ans, dist(p, x, y));
	int gl = t[p].son[0] ? g(t[p].son[0], x, y) : 2e9;
	int gr = t[p].son[1] ? g(t[p].son[1], x, y) : 2e9;
	if(gl < ans) {
		if(gr < ans) {
			if(gl < gr) {
				query(t[p].son[0], x, y);
				if(gr < ans) query(t[p].son[1], x, y);
			}
			else {
				query(t[p].son[1], x, y);
				if(gl < ans) query(t[p].son[0], x, y);
			}
		}
		else query(t[p].son[0], x, y);
	}
	else if(gr < ans) query(t[p].son[1], x, y);
}

高维空间的操作

与邻域查询不同，已经证明在K维空间中修改或者查询某个超长方体中的点的最坏复杂度为 \(O(n^{1-\frac 1 k})\)，最优为 \(O(log_2 n)\)。

操作具体实现方式同平衡树。

不要忘记算自己的贡献和修改自己！（指线段树写习惯了不记得处理当前节点）

（还是放个简单的模板）

int query(int p, int lx, int rx, int ly, int ry) {
	if(! p) return 0;
	if(lx <= t[p].lx && rx >= t[p].rx && ly <= t[p].ly && ry >= t[p].ry) return t[p].val;
	if(lx > t[p].rx || rx < t[p].lx || ly > t[p].ry || ry < t[p].ly) return 0;
	int ret = 0;
	if(t[p].x >= lx && t[p].x <= rx && t[p].y >= ly && t[p].y <= ry) ret += t[p].v;
	return query(t[p].son[0], lx, rx, ly, ry) + query(t[p].son[1], lx, rx, ly, ry) + ret;
}