历史[ZJOI2018]
题目描述&输入/输出格式
题解
首先，没有修改时的答案可以使用树形DP解决
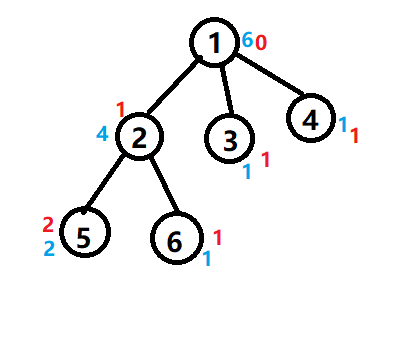
上图中，红色数字表示 \(a_x\)，蓝色数字表示 \(x\) 子树的点权和 \(sum_x\)
观察点 \(2\)，显然只有 \(2,5,6\) "崛起"时才有可能在 \(2\) 发动战争
显然，当操作顺序形如 \(5,2,5,6\) 时，会在 \(2\) 进行三次战争，为最大值。
再来看点 \(1\)，其实我们可以把 \(2,5,6\) 三个点看作一个点，因为 \(2,5,6\) 两两的LCA都为 \(2\)，若某时刻 \(6\) 在 \(5\) 之后一个崛起，则只会在 \(2\) 进行战争，而不会在 \(1\) 进行战争
于是此时可以把 \(sum_2\) 的点权看作 \(2\) 的点权，则此时一种最优的操作顺序为 \(2,1,2,3,2,2\)，在 \(1\) 发动五次战争
接着再来找找规律，发现 \(sum_2=4\)，而存在一种操作方案(即上面的 \(5,2,5,6\))使得相邻两次崛起的城市不相同，所以此时最多在 \(2\) 发动 \(sum_2-1\)次战争
而 \(1\) 就不存在一种相邻元素不相同的操作方案了，因为来自 \(2\) 的操作次数过多
我们记 \(mx[u]=\max(\, \max_{u,v\in E} \ sum[v]\ \, ,\, a[u])\)，比如 \(mx[1]=\max(sum[2],sum[3],sum[4],a[1])=4\)，\(ans[x]\) 为最多在 \(x\) 发动多少次战争，则存在这样一个规律：
若 \(mx[x]*2\ge sum[x]+1\)，则 \(ans[x]=2*(sum[x]-mx[x])\)
否则 \(ans[x]=sum[x]-1\)
然后按照上面的式子进行DP即可拿到30分的暴力分
如何处理修改？
发现每个点 \(x\) 最多有一个儿子 \(y\) 满足 \(sum[y]*2\ge sum[x]+1\)，我们定义这个儿子 \(y\) 为 \(x\) 的"重"儿子
注意 一个点 \(x\) 可能没有任何"重"儿子
维护一棵没有makeroot操作的伪LCT，初始时每个点 \(x\) 向"重"儿子连实边，向其他儿子连轻边
每次修改时，从被修改的点 \(x\) 开始向上access，沿途把某些满足上述条件的轻边修改为重边，把不满足条件的重边修改成轻边
代码如下
inline void calc(int x) {
CCF -= ans[x]; //不要在意变量名
if (son[x]) ans[x] = 2 * (sum[x] - sum[son[x]]); //如果有"重"儿子
else if (a[x] * 2 > sum[x] + 1) ans[x] = 2 * (sum[x] - a[x]); //如果自己点权过大
else ans[x] = sum[x] - 1; //没有点权过大的点或子树
CCF += ans[x];
}
void access(int x, int v) {
a[x] += v;
for (int i = 0; x; i = x, x = fa[x]) {
splay(x);
sum[x] += v;
if (ch[x][0]) sum[ch[x][0]] += v, tag[ch[x][0]] += v;
//给重链上的祖先打标记
//要打标记是因为没有makeroot,没法用split把路径分割出来
//只能通过把重链打上标记来加
if (son[x]) {
stk[top=1] = son[x];
for (int j = son[x]; !isroot(j); j = fa[j]) stk[++top] = fa[j];
while (top) pushdown(stk[top--]);
//pushdown确保sum[son[x]]的值正确
if (sum[son[x]] * 2 <= sum[x] + 1) ch[x][1] = 0, son[x] = 0;
//判断还有没有"重"儿子
}
int F = findroot(i);
//找到轻子树的深度最小的节点
//它的sum才是整棵轻子树的sum
if (sum[F] * 2 > sum[x] + 1) ch[x][1] = F, son[x] = F;
//找到新的"重"儿子
calc(x); //更新答案
}
}
那个CCF变量维护的就是答案
注释应该足够详细了 LCT中的其他操作，例如findroot和pushdown，与原来无异
关于此题时间复杂度
复杂度由于重边轻边的不确定性，非常玄学。。。也许是 \(O(1000ms)\)
代码
#include <bits/stdc++.h>
#define N 400005
using namespace std;
typedef long long ll;
template<typename T>
inline void read(T &num) {
T x = 0, f = 1; char ccf = getchar();
for (; ccf > '9' || ccf < '0'; ccf = getchar()) if (ccf == '-') f = -1;
for (; ccf <= '9' && ccf >= '0'; ccf = getchar()) x = (x << 3) + (x << 1) + (ccf ^ '0');
num = x * f;
}
template<typename T>
void write(T num) {
if (num < 0) putchar('-'), num = -num;
if (num > 9) write(num / 10);
putchar(num % 10 +'0');
}
int n, m;
int head[N], pre[N<<1], to[N<<1], sz;
ll CCF, a[N], sum[N], ans[N];
inline void addedge(int u, int v) {
pre[++sz] = head[u]; head[u] = sz; to[sz] = v;
pre[++sz] = head[v]; head[v] = sz; to[sz] = u;
}
namespace Main{
int fa[N], son[N], ch[N][2];
ll tag[N];
inline void calc(int x) {
CCF -= ans[x];
if (son[x]) ans[x] = 2 * (sum[x] - sum[son[x]]); //如果有"重"儿子
else if (a[x] * 2 > sum[x] + 1) ans[x] = 2 * (sum[x] - a[x]); //如果自己点权过大
else ans[x] = sum[x] - 1; //没有点权过大的点或子树
CCF += ans[x];
}
void dfs(int x) {
sum[x] = a[x];
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == fa[x]) continue;
fa[y] = x; dfs(y);
sum[x] += sum[y];
if (!son[x] || sum[son[x]] < sum[y]) son[x] = y;
}
if (sum[son[x]] * 2 <= sum[x] + 1) son[x] = 0;
calc(x);
ch[x][1] = son[x];
}
inline void pushdown(int x) {
if (!x || !tag[x]) return;
if (ch[x][0]) {
tag[ch[x][0]] += tag[x];
sum[ch[x][0]] += tag[x];
}
if (ch[x][1]) {
tag[ch[x][1]] += tag[x];
sum[ch[x][1]] += tag[x];
}
tag[x] = 0;
}
inline bool isroot(int x) { return ch[fa[x]][0] != x && ch[fa[x]][1] != x; }
inline void rotate(int x) {
int y = fa[x], z = fa[y], k = (ch[y][1]==x);
if (!isroot(y)) ch[z][ch[z][1]==y] = x;
fa[x] = z;
ch[y][k] = ch[x][!k]; fa[ch[x][!k]] = y;
ch[x][!k] = y; fa[y] = x;
}
int stk[N], top;
inline void splay(int x) {
stk[top=1] = x;
for (int i = x; !isroot(i); i = fa[i]) stk[++top] = fa[i];
while (top) pushdown(stk[top--]);
while (!isroot(x)) {
int y = fa[x], z = fa[y];
if (!isroot(y)) ((ch[y][1]==x)^(ch[z][1]==y))?rotate(x):rotate(y);
rotate(x);
}
}
inline int findroot(int x) {
while (ch[x][0]) pushdown(x), x = ch[x][0];
return x;
}
void access(int x, int v) {
a[x] += v;
for (int i = 0; x; i = x, x = fa[x]) {
splay(x);
sum[x] += v;
if (ch[x][0]) sum[ch[x][0]] += v, tag[ch[x][0]] += v;
//给重链上的祖先打标记
//要打标记是因为没有makeroot,没法用split把路径分割出来
//只能通过把重链打上标记来加
if (son[x]) {
stk[top=1] = son[x];
for (int j = son[x]; !isroot(j); j = fa[j]) stk[++top] = fa[j];
while (top) pushdown(stk[top--]);
//pushdown确保sum[son[x]]的值正确
if (sum[son[x]] * 2 <= sum[x] + 1) ch[x][1] = 0, son[x] = 0;
//判断还有没有"重"儿子
}
int F = findroot(i);
//找到轻子树的深度最小的节点
//它的sum才是整棵轻子树的sum
if (sum[F] * 2 > sum[x] + 1) ch[x][1] = F, son[x] = F;
//找到新的"重"儿子
calc(x); //更新答案
}
}
void solve() {
dfs(1);
printf("%lld\n", CCF);
for (int i = 1, x, w; i <= m; i++) {
read(x); read(w);
access(x, w);
printf("%lld\n", CCF);
}
}
}
int main() {
read(n); read(m);
for (int i = 1; i <= n; i++) read(a[i]);
for (int i = 1, u, v; i < n; i++) {
read(u); read(v);
addedge(u, v);
}
Main::solve();
return 0;
}
