字符串[LOJ6517]
题目描述
有 \(N\) 个字符串,每个字符串有一个权值 \(v_i\)。随后给出 \(M\) 次询问,每次对一个区间进行检测。令最长的字符串长度为 \(L\),那么会给出 \(g_1,\cdots,g_L\) 表示每个长度的字符串的「识别值」。
对若干个字符串构成的集合 \(P\) 进行测试的过程如下:
对字符串 \(S\) 定义 \(f(S)\) 表示 \(S\) 在 \(P\) 中以其为前缀出现的串的权值和。 那么如果 \(S\) 在 \(P\) 中作为前缀出现过,并且 \(B*f(S)+A*\mathrm{len}(S)\ge C\),那么则将 \(g_{\mathrm{len}(S)}\) 加入集合。
最后随机选择一个区间 \([x,y](1\le x\le y\le L)\),如果 \([x, y] \bigcap G =\not \emptyset\),那么测试成功,否则测试失败。输出测试成功的概率并用最简分数表示。
特别地,整数 \(k\) 表示为 \(k/1\)。
输入格式
第一行四个数 \(N, A, B, C\)。
接下来一行 \(N\) 个数 \(v_1, \cdots, v_N\)
接下来一行一个数 \(M\)。
接下来 \(M\) 行,每行两个数 \(l,r\),表示对第 \(l\) 到第 \(r\) 个字符串进行测试。
输出格式
\(M\) 个数表示答案。
题解
首先对题目中的 \(n\) 个串建出Trie树。显然如果在某一个 \(P\) 中有一个串以 \(S\) 为前缀出现,那么 \(S\) 一定是Trie树上的一个节点,也就是说Trie树上的每个节点都代表着一个 \(S\)
考虑暴力做法,可以暴力在Trie树上查询 \([l,r]\) 之间的字符串,在Trie树上查询串 \(i\) 时,对Trie树上经过的每个节点 \(S\) ,令 \(f(S)\) 加上 \(v_i\),然后判断是否满足 \(B*f(S)+A*\mathrm{len}(S)\ge C\) ,如果满足就把 \(g_{\mathrm{len}(S)}\) 加入集合 \(G\)。
然后考虑怎么统计答案 显然测试成功的概率=1-测试失败的概率
假设集合 \(G\) 中从小到大排序有 \(b_1,b_2,\cdots,b_k\) 这 \(k\) 个元素,那么测试失败的情况数就是 \(\sum\limits_{i=2}^{k} \dfrac{(b_i-b_{i-1})(b_i-b_{i-1}-1)}{2}\)
因为如果测试失败,则 \([x,y]\) 必然满足:对于某一个 \(i\),\(b_i < x \le y < b_{i+1}\)
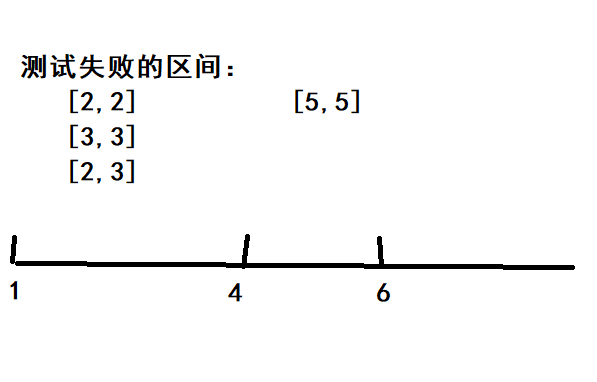
这样我们就得到了一个 \(O(nm)\) 的算法
接下来考虑如何优化
发现询问是区间询问 可以用莫队来处理 需要支持每次在 \(P\) 中加入或删除一个字符串
修改时 \(f(S)\) 显然是可以在Trie树上维护的 可以证明时间复杂度的上限是 \(O(L\sqrt{N})\) 的
考虑如何维护集合 \(G\)
我们设 \(V(x)=\dfrac{x(x+1)}{2}\),那么如果我们在集合 \(G\) 的 \(b_i\) 与 \(b_{i+1}\) 两个元素中插入一个元素 \(y\),那么答案就需要减去 \(V(b_{i+1}-b_i-1)\),然后加上 \(V(b_{i+1}-y-1)\) 和 \(V(y-b_i-1)\)
删除 \(G\) 中的一个元素时同理
于是就可以想到一个用set维护 \(G\) 的naive做法 每次删除/插入元素 \(y\) 时找出它的前驱和后继来修改当前答案
不过这样时间复杂度是 \(O(M\sqrt{N}\log{N})\) 的 我们需要找到一个可以 \(O(1)\) 维护集合 \(G\) 的数据结构
链表这种数据结构 删除元素或查找前驱后继是 \(O(1)\) 的 但是如果要在指定位置插入元素就会很慢
所以我们可以换用只删除不插入的回滚莫队 这样插入操作就去和梁非凡共进晚餐了
然后我们就把 \(O(\log n)\) 修改的set成功换成了 \(O(1)\) 修改的链表 这样就得到了一个上限为 \(O((M+L)\sqrt{N})\) 的大常数?算法 可以通过此题
如果没有找到正确思路,代码非常非常难写。。。所以在这里放上注释过的代码
#include <bits/stdc++.h>
#define N 100005
using namespace std;
typedef long long ll;
template<typename T>
inline void read(T &nnum) {
T x = 0, f = 1; char cch = getchar();
for (; cch > '9' || cch < '0'; cch = getchar()) if (cch == '-') f = -1;
for (; cch <= '9' && cch >= '0'; cch = getchar()) x = (x << 3) + (x << 1) + (cch ^ '0');
nnum = x * f;
}
int n, st[N], ed[N], bst[N], bed[N], g[N<<2], len[N<<2], m, L, Q, sz, bcnt;
char s[N<<2], t[N<<2];
bool vis[N<<2];
int ch[N<<2][26], tot, in[N], rnk[N<<2], pre[N<<2], nxt[N<<2], num[N<<2], top;
ll ans1[N], ans2[N], v[N], cnt[N<<2], nowans, a, b, c;
pair<int, pair<int, int> > changed[N<<2];
void insert(int l, int r) { //建Trie树
int x = 0;
for (int i = l; i <= r; i++) {
if (!ch[x][s[i]-'a']) {
ch[x][s[i]-'a'] = ++tot;
}
x = ch[x][s[i]-'a'];
len[x] = i - l + 1;
}
}
inline ll calc(ll x) {
if (x <= 0) return 0;
else return x * (x + 1) / 2;
}
inline ll V(int x) {
if (!cnt[x]) return 0;
return 1ll * b * cnt[x] + 1ll * a * len[x];
}
void del(int l, int r, int id) { //删除操作,修改点权+修改链表+修改答案
int x = 0;
for (int i = l; i <= r; i++) {
x = ch[x][s[i]-'a'];
cnt[x] -= v[id];
if (V(x) < c && vis[x]) { //若当前节点不满足条件且现在在集合G里
if (!(--num[g[len[x]]])) { //将g[len_S]的出现次数-1
int y = g[len[x]], _pre = pre[y], _nxt = nxt[y];
nowans -= calc(y - _pre - 1) + calc(_nxt - y - 1);
nowans += calc(_nxt - _pre - 1); //修改当前答案
changed[++top] = make_pair(_pre, make_pair(pre[_pre], nxt[_pre]));
changed[++top] = make_pair(_nxt, make_pair(pre[_nxt], nxt[_nxt]));
//记录一下哪些链表元素被修改了 回滚时暴力修改回去
nxt[_pre] = _nxt; pre[_nxt] = _pre;
}
vis[x] = 0;
}
}
}
void add(int l, int r, int id) { //增加操作,仅修改点权,不修改链表和答案
int x = 0;
for (int i = l; i <= r; i++) {
x = ch[x][s[i]-'a'];
cnt[x] += v[id];
if (V(x) >= c && !vis[x]) { //若当前节点已满足条件且不在集合G里
num[g[len[x]]]++;
vis[x] = 1;
}
}
}
struct node{
int l, r, id;
bool operator < (const node bb) const {
return in[l] != in[bb.l] ? l < bb.l : r > bb.r;
//由于是只删不增的回滚莫队 所以右端点从大到小排序
}
} q[N];
int main() {
read(n); read(a); read(b); read(c);
sz = sqrt(n); bcnt = 1;
for (int i = 1; i <= n; i++) {
if (i % sz == 1) bst[bcnt] = i;
in[i] = bcnt;
if (i % sz == 0) bed[bcnt] = i, bcnt++;
//表示一个块的起始和结束位置
}
if (n % sz == 0) bcnt--;
bed[bcnt] = n;
for (int i = 1; i <= n; i++) {
read(v[i]);
}
for (int i = 1, l; i <= n; i++) {
scanf("%s", t + 1); l = strlen(t + 1);
L = max(L, l);
st[i] = m + 1;
for (int j = 1; j <= l; j++) {
s[++m] = t[j];
}
ed[i] = m;
}
for (int i = 1; i <= L; i++) {
read(g[i]);
}
read(Q);
for (int i = 1; i <= Q; i++) {
read(q[i].l); read(q[i].r);
q[i].id = i;
}
sort(q + 1, q + Q + 1);
for (int i = 1; i <= n; i++) {
insert(st[i], ed[i]);
}
num[L+1] = 114514; //哼哼啊啊啊啊
int now = 1, nl = 0, nr = 0;
for (int i = 1; i <= bcnt; i++) {
nowans = 0;
for (int j = bst[i]; j <= n; j++) {
add(st[j], ed[j], j); //将 当前块的起始位置 ~ N 的所有字符串加入集合P
}
int lst = 0;
for (int j = 1; j <= L + 1; j++) {
if (num[j]) { //预处理出初始链表和初始答案
pre[j] = lst; nxt[lst] = j;
nowans += calc(j - lst - 1);
lst = j;
}
}
nr = n; //当前右端点从N开始向左移动
while (in[q[now].l] == i) {
while (nr > q[now].r) del(st[nr], ed[nr], nr), nr--;
top = 0; //右端点的修改不用回滚!
ll tmp = nowans; //记录当前答案 方便查询完这次之后直接改回去
nl = bst[i];
while (nl < q[now].l) del(st[nl], ed[nl], nl), nl++;
//删除时 点权,链表,答案可以一起修改 但是撤销时最好要一个一个撤销比较好写
ans1[q[now].id] = nowans;
ans2[q[now].id] = 1ll * L * (L+1) / 2;
for (int j = q[now].l - 1; j >= bst[i]; j--) add(st[j], ed[j], j); //撤销对Trie树上点权的修改
while (top) { //撤销对链表的修改
pre[changed[top].first] = changed[top].second.first;
nxt[changed[top].first] = changed[top].second.second;
top--;
}
nowans = tmp; //撤销对答案的修改
now++;
}
while (nr >= bst[i]) { //把剩余字符串全部删掉 相当于让P集合回到空集
del(st[nr], ed[nr], nr);
nr--;
}
}
for (int i = 1; i <= Q; i++) {
ans1[i] = ans2[i] - ans1[i];
if (ans1[i] == 0) puts("0/1");
else if (ans1[i] == ans2[i]) puts("1/1");
else {
ll gcd = __gcd(ans1[i], ans2[i]);
ans1[i] /= gcd; ans2[i] /= gcd;
printf("%lld/%lld\n", ans1[i], ans2[i]);
}
}
return 0;
}


