世界树[HNOI2014]
题目描述
题目背景太长不放 传送门
给你一棵\(n\)个节点的树,有\(q\)次询问,每次指定\(m_i\)个节点为关键节点;对于任意一个节点,它被距离自己树上距离最近的那个关键节点管辖;输出每个关键节点各管辖多少个节点
\(n,\, q \le 300000\),\(\sum m_i\le 300000\)
题解
看到\(\sum m_i\le 300000\)想到什么了?虚树!
所以我们把关键节点的虚树建出来,然后考虑怎么进行DP
(为了方便我们要求\(1\)号节点一定要在虚树里)
注意这里建虚树要加上一个边权,表示原树上两个节点的距离
首先,对于每个虚树上的点,我们求出它们各自被哪个关键节点管辖,记为\(in_x\),这个比较简单就不讲了;把点到管辖它的关键节点之间的距离记为\(dis_x\)
然后我们考虑虚树上的一条边\(u\rightarrow v\),\(u\)是\(v\)的父亲
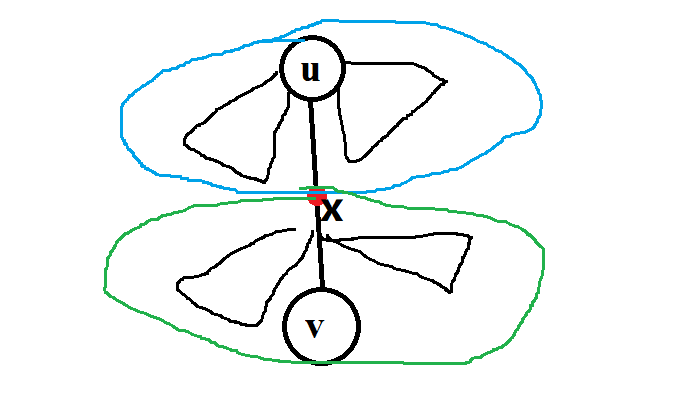
这条边上一定存在一个断点\(x\),使得上面蓝圈那部分的所有节点被\(in_u\)管辖,下面绿圈那部分被\(in_v\)管辖
我们怎么求出这个断点\(x\)呢?
如果一个\(u\rightarrow v\)链上的点\(y\)在绿圈部分,\(y\)离\(u\)的距离是\(a\),离\(v\)的距离是\(b\),那么一定满足:
- \(in_u\)编号小于\(in_v\)时,\(y\)须满足\(in_u+a>in_v+b\)
- \(in_u\)编号大于\(in_v\)时,\(y\)须满足\(in_u+a\ge in_v+b\)
由于我们之前记录了虚树上面每条边的实际长度,所以我们知道\(b\),就可以直接用\(u\rightarrow v\)的长度减去\(b\)得到\(a\)
这样我们就能\(O(1)\)找出一个距离\(v\)最远的\(y\),它就是那个断点,可以从\(v\)开始用倍增往上跳父亲找到
然后怎么进行转移呢?初始时设\(ans[in_1]=n\),每次枚举到一条边\(u\rightarrow v\)时,找出断点\(x\),然后\(ans[in_u]\)减去\(size_x\),\(ans[in_v]\)加上\(size_x\);这里\(size_x\)表示\(x\)子树的大小
可以这样理解:由于我们是按照深搜顺序进行dp的,所以搜到这条边时整个\(u\)的子树都是在由\(in_u\)管辖,现在我们要把下面的那部分分给\(in_v\)管辖
时间复杂度\(O(n\log n)\),是倍增求lca以及向上跳的复杂度
码量巨大,我写数据结构题都写不到这么长。。。
代码
#include <bits/stdc++.h>
using namespace std;
template<typename T>
inline void read(T &num) {
T x = 0, f = 1; char ch = getchar();
for (; ch > '9' || ch < '0'; ch = getchar()) if (ch == '-') f = -1;
for (; ch <= '9' && ch >= '0'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ '0');
num = x * f;
}
int n, m, cnt;
int head[300005], pre[600005], to[600005], val[600005], sz;
int dfn[300005], siz[300005], d[300005], p[300005][21], tme;
int q[300005], tmp[300005], stk[300005], top, reset[1000005], tot;
int mn[300005], mnind[300005], ans[300005];
bool point[300005];
inline void addedge(int u, int v, int w) {
reset[++tot] = u; reset[++tot] = v; //奇妙重置数组方法
pre[++sz] = head[u]; head[u] = sz; to[sz] = v; val[sz] = w;
pre[++sz] = head[v]; head[v] = sz; to[sz] = u; val[sz] = w;
}
void dfs(int x) {
siz[x] = 1; dfn[x] = ++tme;
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == p[x][0]) continue;
d[y] = d[x] + 1; p[y][0] = x;
dfs(y);
siz[x] += siz[y];
}
}
inline int LCA(int x, int y) {
if (d[x] < d[y]) swap(x, y);
for (int i = 20; i >= 0; i--) {
if (d[x] - (1 << i) >= d[y]) x = p[x][i];
}
if (x == y) return x;
for (int i = 20; i >= 0; i--) {
if (p[x][i] != p[y][i]) {
x = p[x][i];
y = p[y][i];
}
}
return p[x][0];
}
inline int jumpup(int x, int t) {
for (int i = 20; i >= 0; i--) {
if (t >= (1 << i)) {
t -= (1 << i);
x = p[x][i];
}
}
return x;
}
bool cmp(int x, int y) {
return dfn[x] < dfn[y];
}
void buildtree() {
for (int i = 1; i <= tot; i++) { //奇妙重置数组方法
head[reset[i]] = ans[reset[i]] = 0;
mn[reset[i]] = 0x3f3f3f3f;
}
tot = sz = 0;
sort(q + 1, q + cnt + 1, cmp);
stk[top=1] = 1;
for (int i = 1; i <= cnt; i++) {
if (q[i] == 1) continue;
if (top == 1) {
stk[++top] = q[i];
continue;
}
int lca = LCA(stk[top], q[i]);
while (top > 1 && dfn[stk[top-1]] >= dfn[lca]) {
addedge(stk[top], stk[top-1], abs(d[stk[top]] - d[stk[top-1]]));
top--;
}
if (stk[top] != lca) {
addedge(stk[top], lca, abs(d[stk[top]]-d[lca]));
stk[top] = lca;
}
stk[++top] = q[i];
}
while (top > 1) {
addedge(stk[top], stk[top-1], abs(d[stk[top]] - d[stk[top-1]]));
top--;
}
}
void dp1(int x, int fa) {
if (point[x]) mn[x] = 0, mnind[x] = x;
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == fa) continue;
dp1(y, x);
if (mn[x] > mn[y] + val[i]) {
mn[x] = mn[y] + val[i];
mnind[x] = mnind[y];
} else if (mn[x] == mn[y] + val[i]) {
if (mnind[x] > mnind[y]) mnind[x] = mnind[y];
}
}
}
void dp2(int x, int fa) {
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == fa) continue;
if (mn[y] > mn[x] + val[i]) {
mn[y] = mn[x] + val[i];
mnind[y] = mnind[x];
} else if (mn[y] == mn[x] + val[i]) {
if (mnind[y] > mnind[x]) mnind[y] = mnind[x];
}
dp2(y, x);
}
}
void dp3(int x, int fa) {
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == fa) continue;
if (mnind[x] == mnind[y]) {
} else {
int dis = val[i] + mn[y] - mn[x], num = 0;
if (mnind[x] < mnind[y]) {
num = dis / 2;
} else num = (dis-1) / 2;
num = min(num, val[i]); num = max(num, 0);
num = val[i] - num - 1;
int z = jumpup(y, num); //z即是这条边的断点
ans[mnind[x]] -= siz[z]; ans[mnind[y]] += siz[z];
}
}
for (int i = head[x]; i; i = pre[i]) {
if (to[i] != fa) dp3(to[i], x);
}
}
void solve() {
buildtree(); //建虚树
dp1(1, 0);
dp2(1, 0); //两遍dfs求出虚树上每个点被哪个点管辖
ans[mnind[1]] = siz[1];
dp3(1, 0); //进行dp
for (int i = 1; i <= cnt; i++) {
printf("%d ", ans[tmp[i]]);
} puts("");
}
int main() {
read(n);
for (int i = 1, u, v; i < n; i++) {
read(u); read(v);
addedge(u, v, 0);
}
dfs(1); //预处理出节点深度,倍增数组,dfs序等
for (int l = 1; (1 << l) <= n; l++) {
for (int i = 1; i <= n; i++) {
p[i][l] = p[p[i][l-1]][l-1];
}
}
read(m);
for (int i = 1; i <= m; i++) {
read(cnt);
for (int j = 1; j <= cnt; j++) {
read(q[j]);
point[q[j]] = 1;
tmp[j] = q[j];
}
solve();
for (int j = 1; j <= cnt; j++) {
point[q[j]] = 0;
}
}
return 0;
}


