优秀的拆分「NOI2016」
题目描述
如果一个字符串可以被拆分为 \(\text{AABB}\) 的形式,其中 \(\text{A}\) 和 \(\text{B}\) 是任意非空字符串,则我们称该字符串的这种拆分是优秀的。
例如,对于字符串 \(\texttt{aabaabaa}\) ,如果令 \(\text{A}=\texttt{aab}\),\(\text{B}=\texttt{a}\),我们就找到了这个字符串拆分成 \(\text{AABB}\) 的一种方式。
一个字符串可能没有优秀的拆分,也可能存在不止一种优秀的拆分。
比如我们令 \(\text{A}=\texttt{a}\),\(\text{B}=\texttt{baa}\),也可以用 \(\text{AABB}\) 表示出上述字符串;但是,字符串 \(\texttt{abaabaa}\) 就没有优秀的拆分。
现在给出一个长度为 \(n\) 的字符串 \(S\),我们需要求出,在它所有子串的所有拆分方式中,优秀拆分的总个数。这里的子串是指字符串中连续的一段。
以下事项需要注意:
- 出现在不同位置的相同子串,我们认为是不同的子串,它们的优秀拆分均会被记入答案。
- 在一个拆分中,允许出现 \(\text{A}=\text{B}\)。例如 \(\texttt{cccc}\) 存在拆分 \(\text{A}=\text{B}=\texttt{c}\)。
- 字符串本身也是它的一个子串。
输入格式
每个输入文件包含多组数据。
输入文件的第一行只有一个整数 \(T\),表示数据的组数。
接下来 \(T\) 行,每行包含一个仅由英文小写字母构成的字符串 \(S\),意义如题所述。
输出格式
输出 \(T\) 行,每行包含一个整数,表示字符串 \(S\) 所有子串的所有拆分中,总共有多少个是优秀的拆分。
\(n\le 30000\)
题解
太良心了
\(85\%\)的点\(n\le 500\),直接\(O(n^3)\)暴力枚举区间+断点用哈希判断
然后只要稍微动动脑子:设\(a[i]\)表示以\(i\)结尾的\(\text{AA}\)串个数,\(b[i]\)表示以\(i\)开头的\(\text{AA}\)串个数,那么答案就是\(\sum\limits_{i=1}^{n-1} a[i]*b[i+1]\)
\(O(n^2)\) 95分到手
最后五分如果想不出来不拿也感觉无所谓。。。最后五分确实不好想
所以开始说正解:
上面的95分解法问题就在于\(a[N],\ b[N]\),我们需要\(O(n^2)\)的时间求出来,考虑怎么样求得更快
我们枚举一个\(len\)表示我们现在想找到那些长度为\(2*len\)的\(\text{AA}\)串
然后在原串上每隔\(len\)放一个断点
我们枚举相邻的两个断点\(i,j\),现在我们想要知道 以\(i\)开头的后缀与以\(j\)开头的后缀的最长公共前缀(LCP) 和 以\(i\)结尾的前缀与以\(j\)结尾的前缀的最长公共后缀(LCS)
LCP可以用后缀数组求;LCS也可以,把原数组翻转之后就变成后缀的LCP了,所以这两个都是可以用ST表\(O(1)\)求出的
那么现在我们求出了这两个值
情况1
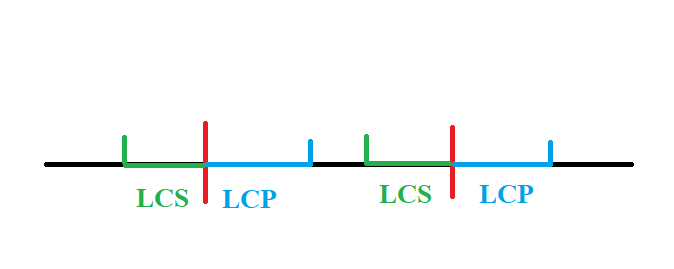
对于这种情况,即\(LCP+LCS-1<len\),我们是找不出\(\text{AA}\)串的
情况2
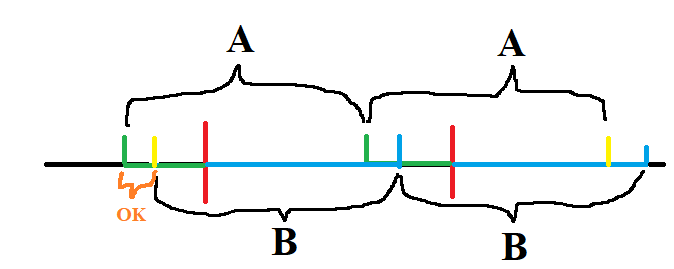
用脚画图 不愧是我
\(LCP+LCS-1<len\),这个时候就有很多的长为\(2*len\)的\(\text{AA}\)串了,图中画出的\(\text{AA},\ \text{BB}\)就是最靠左和最靠右的两个这样的串
实际上,我画了"OK"的那个橙色区间的每一个点都是一个长为\(2*len\)的\(\text{AA}\)串的开头,应该很好理解吧。。。
如何找哪一段是合法\(\text{AA}\)串的结尾也同理
所以实际上每次就是把\(a[N]\)和\(b[N]\)的某一段全部加一 用差分来维护一下就行了
最后来看一下时间复杂度
后缀数组+ST表是\(O(n\log n)\)
\(\frac{n}{1}+\frac{n}{2}+\frac{n}{3}+\dots+\frac{n}{n}\) 我记得差不多就是\(O(n \log n)\)吧。。。可能要稍微大一点
总之\(n\le 30000\)的数据是完全没有压力的
注意多组数据初始化数组!注意多组数据初始化数组!注意多组数据初始化数组!
代码
#include <bits/stdc++.h>
#define N 60005
using namespace std;
int t, n, nn;
char s[N];
int a[N], b[N];
int sa[N], sa2[N], rnk[N], sum[N], key[N], height[N], ST[N][21];
inline bool check(int *num, int aa, int bb, int l) {
if (aa + l > n || bb + l > n) return false; //多组数据,一定要加!
return num[aa] == num[bb] && num[aa+l] == num[bb+l];
}
void DA() {
int i, j, p, m = 128;
for (i = 1; i <= m; i++) sum[i] = 0;
for (i = 1; i <= n; i++) sum[rnk[i]=s[i]]++;
for (i = 2; i <= m; i++) sum[i] += sum[i-1];
for (i = n; i; i--) sa[sum[rnk[i]]--] = i;
for (j = 1; j <= n; j <<= 1, m = p) {
for (p = 0, i = n - j + 1; i <= n; i++) sa2[++p] = i;
for (i = 1; i <= n; i++) if (sa[i] - j > 0) sa2[++p] = sa[i] - j;
for (i = 1; i <= n; i++) key[i] = rnk[sa2[i]];
for (i = 1; i <= m; i++) sum[i] = 0;
for (i = 1; i <= n; i++) sum[key[i]]++;
for (i = 2; i <= m; i++) sum[i] += sum[i-1];
for (i = n; i; i--) sa[sum[key[i]]--] = sa2[i];
for (swap(sa2, rnk), p = 2, rnk[sa[1]] = 1, i = 2; i <= n; i++) {
rnk[sa[i]] = check(sa2, sa[i-1], sa[i], j) ? p - 1 : p++;
}
}
}
void geth() {
int p = 0;
for (int i = 1; i <= n; i++) rnk[sa[i]] = i;
for (int i = 1; i <= n; i++) {
if (p) p--;
int j = sa[rnk[i]-1];
while (s[i+p] == s[j+p] && i + p <= n && j + p <= n) p++; //多组数据,一定要加!
height[rnk[i]] = p;
}
}
void preST() {
for (int i = 1; i <= n; i++) ST[i][0] = height[i];
for (int l = 1; (1 << l) <= n; l++) {
for (int i = 1; i + (1<<l) - 1 <= n; i++) {
ST[i][l] = min(ST[i][l-1], ST[i+(1<<(l-1))][l-1]);
}
}
}
inline int QST(int x, int y) {
if (x > y) swap(x, y); x++;
int l = log2(y - x + 1);
return min(ST[x][l], ST[y-(1<<l)+1][l]);
}
inline int LCP(int x, int y) { return QST(rnk[x], rnk[y]); }
inline int LCS(int x, int y) { return QST(rnk[n-x+1], rnk[n-y+1]); }
void Solve() {
for (int l = 1; l * 2 <= nn; l++) {
for (int i = 1, j = i + 1; j * l <= nn; i++, j++) {
int lcp = min(LCP(i*l, j*l), l), lcs = min(LCS(i*l, j*l), l);
if (lcp + lcs - 1 >= l) {
a[j*l+l-lcs]++; a[j*l+lcp]--;
b[i*l-lcs+1]++; b[i*l-l+lcp+1]--;
}
}
}
for (int i = 1; i <= nn; i++) {
a[i] += a[i-1];
b[i] += b[i-1];
}
long long ans = 0;
for (int i = 1; i < nn; i++) {
ans += 1ll * a[i] * b[i+1];
}
printf("%lld\n", ans);
}
int main() {
scanf("%d", &t);
while (t--) {
memset(a, 0, sizeof(a)); memset(b, 0, sizeof(b));
scanf("%s", s + 1);
n = strlen(s + 1);
s[n+1] = '$';
for (int i = n + 2; i <= 2 * n + 1; i++) {
s[i] = s[2 * n - i + 2];
}
nn = n;
n = (n<<1|1);
DA(); geth(); preST();
Solve();
}
return 0;
}


