玩具装箱[HNOI2008]
题目描述
P 教授要去看奥运,但是他舍不下他的玩具,于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩,其可以将任意物品变成一堆,再放到一种特殊的一维容器中。
P 教授有编号为 \(1 \cdots n\) 的 \(n\) 件玩具,第 \(i\) 件玩具经过压缩后的一维长度为 \(C_i\)。
为了方便整理,P教授要求:
- 在一个一维容器中的玩具编号是连续的。
- 同时如果一个一维容器中有多个玩具,那么两件玩具之间要加入一个单位长度的填充物。形式地说,如果将第 \(i\) 件玩具到第 \(j\) 个玩具放到一个容器中,那么容器的长度将为 \(x=j-i+\sum\limits_{k=i}^{j}C_k\)
制作容器的费用与容器的长度有关,根据教授研究,如果容器长度为 \(x\),其制作费用为 \((x-L)^2\)。其中 \(L\) 是一个常量。P 教授不关心容器的数目,他可以制作出任意长度的容器,甚至超过 \(L\)。但他希望所有容器的总费用最小。
输入格式
第一行有两个整数,用一个空格隔开,分别代表 \(n\) 和 \(L\)。
第 \(2\) 到 第 \((n + 1)\) 行,每行一个整数,第 \((i + 1)\) 行的整数代表第 \(i\) 件玩具的长度 \(C_i\)。
输出格式
输出一行一个整数,代表所有容器的总费用最小是多少。
补一道斜率优化模板题QWQ
题解
设\(dp[i]\)表示装前\(i\)个玩具的最小花费,\(sum[i]\)为前\(i\)个玩具的\(C_i\)之和
转移方程非常显然:\(dp[i]=\min_{j=0}^{i-1} dp[j]+(sum[i]-sum[j]+i-j-1-L)^2\)
一个经典的1D/1D动态规划
直接转移是\(n^2\)的 由于这题转移方程有平方项所以也不能直接用单调队列 看到有二次项的1D/1D动态规划就要考虑使用斜率优化
接下来说说什么是斜率优化
我们给原方程变个形
设\(A_i=sum[i]+i,B_i=sum[i]+i+L+1\)
那个\(\min\)看着麻烦 先扔掉了
那么现在有 \(dp[i]=dp[j]+(A_i-B_j)^2\)
拆开完全平方,得到\(dp[i]=dp[j]+A_i^2-2*A_i*B_j+B_j^2\)
把只含\(j\)的全部移到左边,得到\((dp[j]+B_j^2)=(2*A_i)*B_j+(dp[i]-A_i^2)\)
为什么要打上括号?
看一下直线的斜截式的方程\(y=kx+b\) 我们的转移方程里 让\(y=dp[j]+B_j^2, k=(2*A_i), x=B_j, b=(dp[i]-A_i^2)\) 就是一条直线方程
其中\(j<i\),所以\(dp[j]\)我们已经算出来了 所以\(y,k,x\)都是已知的
\(j<i\)的\(j\)不止一个 所以实际上现在在二维平面上有很多个点 第\(j\)个点的坐标为\((B_j, dp[j]+B_j^2)\)
由于\(A_i^2\)已知,我们希望\(dp[i]\)尽量小就是要让\(dp[i]-A_i^2\)尽量小 也就是截距要尽量小
所以我们现在需要在二维平面上选一个点\(j\) 过它画一条斜率为\(2*A_i\)的直线 直线的截距即是\(dp[i]-A_i^2\)
比如像是这样?
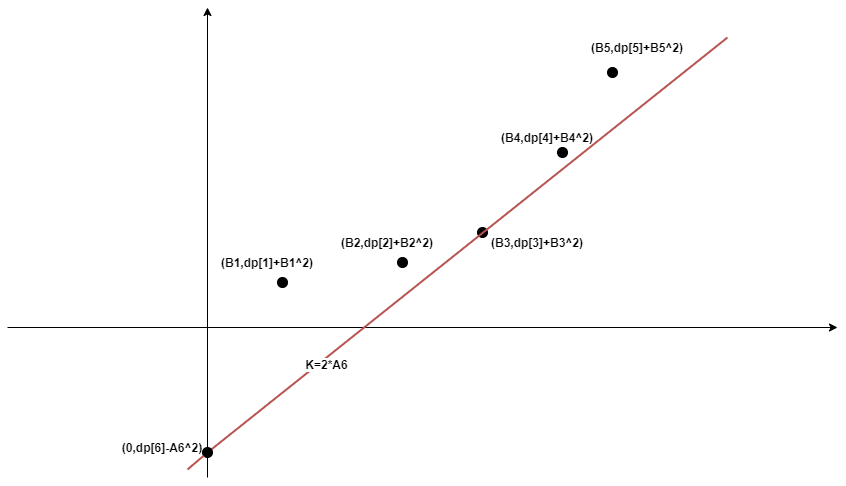
这是我们在推\(dp[6]\) 当直线斜率为\(2*A_6\)时 我们发现让它经过第3个点得到的截距最小
从而我们就能让\(dp[6]\)的值从\(dp[3]\)转移过来 然后在图中加入第6个点\((B_6,dp[6]+B_6^2)\)
问题来了 我们怎么快速求得经过哪个点会使得截距最小?
这题有一个很重要的性质:\(x\),即\(B_j\); 以及\(k\),即\(2*A_i\)(满足决策单调性!!!); 这两个都是递增的 (没有这个性质就不能用单调队列了 而是用cdq分治之类的算法)
所以第\(i\)个点一定在第\(i-1\)个点右边 而且直线的斜率也只会越来越大
我们对于已经存在的点 维护一个下凸壳 放在单调队列里
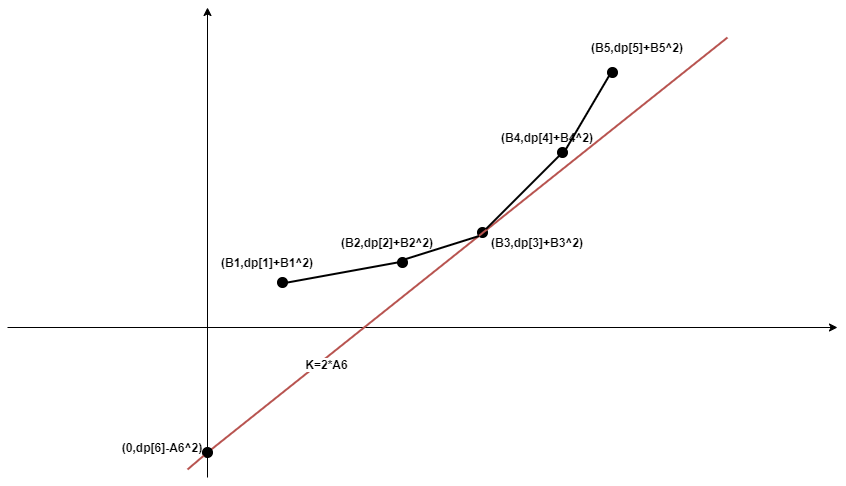
我们记第\(j\)个点为\(p_j\),记相邻两点连成的直线的斜率为 \(\operatorname{slope}(p_{j-1},p_j)\)
假设当前在推\(dp[6]\)的值 则我们要画一条斜率为\(2*A_6\)的直线
观察一下 我们发现 找到凸壳上第一个\(j\)满足\(\operatorname{slope}(p_{j},p_{j+1})>2*A_6\),过这个点画直线就是最优的 这个例子中这个点就是3
而且还有一个之前提到的性质 \(2*A_i\)是单增的 所以如果某个\(\operatorname{slope}(p_{j},p_{j+1})<2*A_6\) 那么对于之后的\(i>6\),也一定是\(\operatorname{slope}(p_{j},p_{j+1})<2*A_i\) 所以\(j\)这个点无论如何都不再会被用到 就直接从队列里弹出 ①
最后单调队列的队头就是最优的决策点 我们算出\(dp[6]\)的值 由于\(B_j\)是递增的 我们可以直接把\((B_6,dp[6]+B_6^2)\)拿去更新这个凸包
更新时\((B_6,dp[6]+B_6^2)\)可能在这里
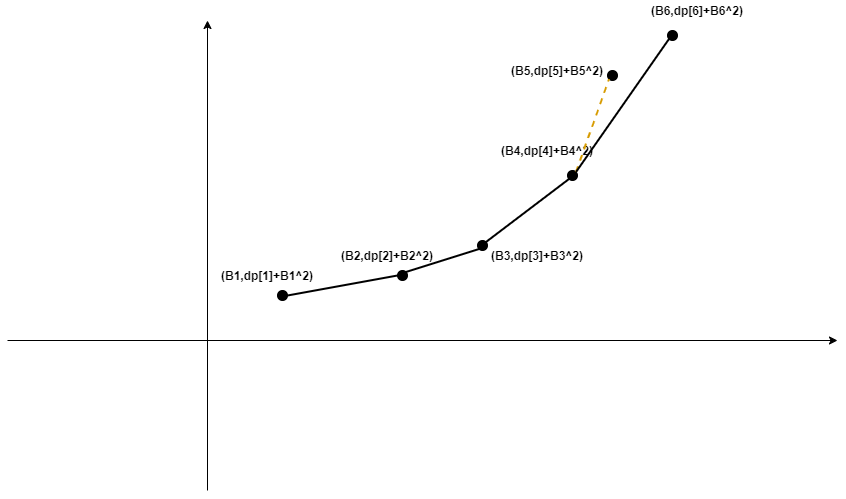
此时 \(\operatorname{slope}(p_{4},p_{5})>\operatorname{slope}(p_{5},p_{6})\)
为了维护凸包的性质 我们把\(4\rightarrow 5\)这条边从队列里删掉(即把5弹出) 然后再加入6 ②
实现起来其实很简单 结合注释看看吧
每个点最多出队入队一次 时间复杂度\(O(n)\)
不知道为什么原题数据规模这么小
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
template<typename T>
inline void read(T &num) {
T x = 0, f = 1; char ch = getchar();
for (; ch > '9' || ch < '0'; ch = getchar()) if (ch == '-') f = -1;
for (; ch <= '9' && ch >= '0'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ '0');
num = x * f;
}
int n, head, tail, q[100005];
ll l, c[100005], a[100005], b[100005], dp[100005];
struct point{
ll x, y;
point() {}
point(ll xx, ll yy): x(xx), y(yy) {}
} p[100005];
double slope(point A, point B) {
return 1.0 * (A.y - B.y) / (A.x - B.x);
}
int main() {
read(n); read(l);
b[0] = l + 1;
for (int i = 1; i <= n; i++) {
read(c[i]);
a[i] = a[i-1] + c[i] + 1; //预处理Ai,Bi
b[i] = b[i-1] + c[i] + 1;
}
head = tail = 1;
p[0] = point(b[0], b[0] * b[0]); //开始时队列里只有0号点
q[1] = 0;
for (int i = 1; i <= n; i++) {
while (head < tail && slope(p[q[head]], p[q[head+1]]) < 2.0 * a[i] + 1e-8) head++; //文中注释1
dp[i] = dp[q[head]] + (a[i] - b[q[head]]) * (a[i] - b[q[head]]); //q[head]为最佳决策点 直接用原转移方程更新dp[i]
p[i] = point(b[i], dp[i] + b[i] * b[i]); //确定i号点的位置
while (head < tail && slope(p[q[tail-1]], p[q[tail]]) + 1e-8 > slope(p[q[tail]], p[i])) tail--; //文中注释2
q[++tail] = i;
}
printf("%lld\n", dp[n]);
return 0;
}


