遗产「CF 787D」

【题目描述】
Rick和他的同事制作了一种新的放射性配方，很多坏人都跟着他们。所以Rick想要在坏人抓住他们之前将他的遗产交给Morty。他们的宇宙中有 \(n\) 个行星从 \(1\) 到 \(n\) 编号。Rick在行星编号 \(s\)（地球），他不知道Morty在哪里。众所周知，里克拥有一支门卫枪。有了这把枪，他就可以打开从他所在行星到任何其他星球（包括那个星球）的单向门。但这支枪有一些限制，因为他仍在使用免费试用版。

默认情况下，他不能用这把枪打开任何门。网站上有q个这些枪支的商品。每次购买时，您只能使用一次，但如果您想再使用它，可以再次购买。网站上的出售的枪有三种类型：

1.通过这种类型的枪，您可以打开从行星 \(v\) 到行星 \(u\) 的门户。

2.通过这种类型的枪，您可以打开从行星 \(v\) 到任何行星的入口，其范围为 \([l,r]\) 。

3.通过这种类型的枪，您可以从任何行星打开门，其索引范围为 \([l,r]\) 到行星 \(v\) 。

Rick不知道Morty在哪里，但Unity会告诉他，他希望在他找到并立即开始他的旅程时做好准备。因此，对于每个行星（包括地球本身），他想知道从地球到这个星球所需的最低金额。

【输入格式】
第一行包含三个整数 \(n,q,s(1\leq  n, q \leq  10^5, 1 \leq  s \leq  n)\) 分别代表星球数量，枪出售数量，地球的索引。接下来 \(q\) 行，每行从销售类型 \(t (1 \leq  t \leq 3)\) 开始。

【输出格式】
输出 \(n\) 个整数，用空格隔开。第 \(i\) 个答案，代表地球到编号为 \(i\) 的星球的最小花费是多少？如果无法到达输出 \(-1\)

题解

如果直接暴力建图 边数的数量是 \(n^2\) 级别的 不能接受

发现第2，3种枪都是一段区间匹配 我们可以用线段树优化建图

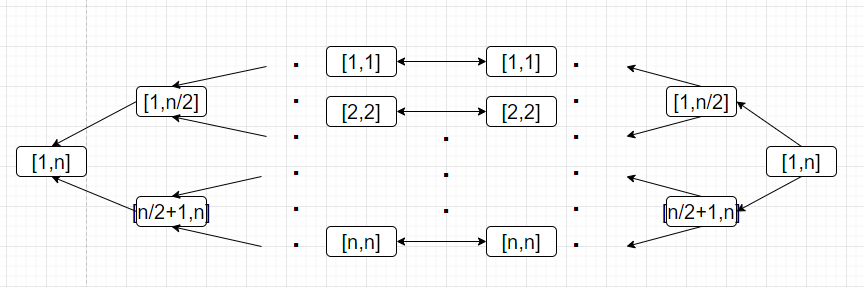
所以我们建了一个这样的图出来 这个图中所有边的边权都是 \(0\)

左右两边各是一棵线段树 其中右边的线段树是父节点向儿子连有向边 左边的线段树相反 然后两棵树的对应叶子节点之间连无向边 我们把右边的树叫做 \(in\) 左边的叫做 \(out\)

这个有什么用呢？我们来研究一下性质：对于 \(in\) 的一个非叶子节点\([l,r]\) 显然 从这个节点可以走 \(0\) 的距离到达任意一个 \(l\le i\le r\) 的叶子节点 \([i,i]\)

而对于 \(out\) 的一个叶子节点 \([x,x]\) 从这个节点可以走 \(0\) 的距离到达任意一个 \(l\le x\le r\) 的非叶子节点 \([l,r]\)

也就是说 对于题目中的第2种边 我们可以将 \(in\) 树的节点 \([v,v]\) 连向 \(in\) 中的一些节点 这些节点代表的区间的并集恰好组成边要求的 \([l,r]\) 这样其实就等价于我们从 \([v,v]\) 向每个 \(l\le i\le r\) 的 \([i,i]\) 都连了一条边 但是通过线段树这样连我们只需要连最多 \(\log n\) 条

比如说 \(n=8\) 现在有一条2类边 可以从 \(3\) 走向 \([1,7]\) 中的任意一个 那么我们就将 \(in\) 树中的 \([3,3]\) 向 \([1,4],[5,6],[7,7]\) 分别连有向边

第3类边也很相似 比如说有一条3类边 可以从 \([1,7]\) 中任意一个走向 \(3\) 那么我们把 \(out\) 树中的 \([1,4],[5,6],[7,7]\) 分别向 \([3,3]\) 连有向边

对于第一类边 如果这条边从 \(u\) 到 \(v\) 就直接从 \(in\) 中的节点 \([u,u]\) 向 \(out\) 的节点 \([v,v]\) 连有向边

答案即是从 \(in\) 中的节点 \([s,s]\) 开始跑单源最短路 到 \(out\) 每个叶子节点的最短距离

举个例子吧

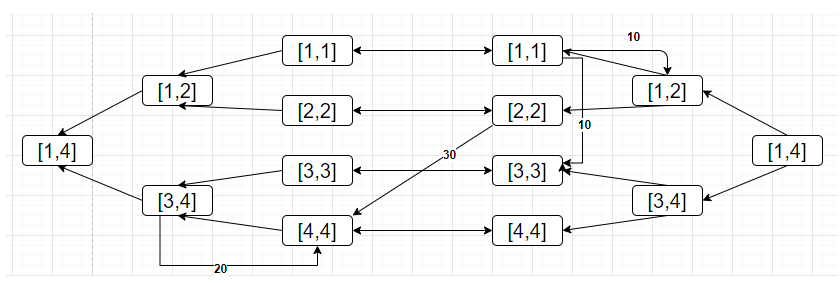
首先 有一条1类边 从 \(2\) 走到 \(4\) 花费为 \(30\) 我们把 \(in\) 的 \([2,2]\) 连向 \(out\) 的 \([4,4]\) 这条边叫做①

有一条2类边 可以从 \(1\) 走到 \([1,3]\) 花费为 \(10\) 我们在 \(in\) 图中从 \([1,1]\) 分别连向 \([1,2],[3,3]\) 这条边叫做②

有一条3类边 从 \([3,4]\) 走向 \(4\) 花费为 \(20\) 我们把 \(out\) 的 \([3,4]\) 连向 \([4,4]\) 这条边叫做③

假设我们现在要从 \(1\) 走到 \(4\) ，我们来看看怎么走：

先通过②从 \(1\) 走到 \(2\) 在图中即是从 \([1,1]\) 走到 \([1,2]\) 再走到 \([2,2]\)

然后走①从 \(2\) 到 \(4\) ，这种走法的总花费是 \(10+30=40\)

再看看另一种走法

通过②从 \(1\) 走到 \(3\) 在图中就是 \([1,1] \rightarrow [3,3]\)

再通过③从 \(3\) 走到 \(4\) 在图中就是 \([3,3] \rightarrow [3,3] \rightarrow [3,4] \rightarrow [4,4]\) 到达目标点

花费是 \(10+20=30\)

所以第二种走法是 \(1\rightarrow 4\) 的最短路

加第2，3类边的时候像线段树区间查询一样找到需要连边的区间就可以了 具体见代码

加完所有边之后一遍单源最短路就可以了 Dijkstra和某死了的算法应该都没问题

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

struct segtree{
	int l, r, id;
} in[400005], out[400005];

int cnt;

#define lson ind<<1
#define rson ind<<1|1

int head[1000005], pre[2000005], to[2000005], sz;
int pos[2][100005];
ll val[2000005];

inline void addedge(int u, int v, ll w) {
	pre[++sz] = head[u]; head[u] = sz; to[sz] = v; val[sz] = w;
}

void build(segtree *tr, int ind, int l, int r, int tp) {
	tr[ind].l = l, tr[ind].r = r, tr[ind].id = ++cnt;
	if (l == r) {
		pos[tp][l] = tr[ind].id;
		return;
	}
	int mid = (l + r) >> 1;
	build(tr, lson, l, mid, tp);
	build(tr, rson, mid+1, r, tp);
	if (!tp) {
		addedge(tr[ind].id, tr[lson].id, 0);
		addedge(tr[ind].id, tr[rson].id, 0);
	} else {
		addedge(tr[lson].id, tr[ind].id, 0);
		addedge(tr[rson].id, tr[ind].id, 0);
	}
}

void query(segtree *tr, int ind, int x, int y, int p, ll w, int tp) {
	int l = tr[ind].l, r = tr[ind].r;
	if (x <= l && r <= y) {
		if (!tp) addedge(p, tr[ind].id, w);
		else addedge(tr[ind].id, p, w);
		return;
	}
	int mid = (l + r) >> 1;
	if (x <= mid) query(tr, lson, x, y, p, w, tp);
	if (mid < y) query(tr, rson, x, y, p, w, tp);
}

int n, q, s;
bool vis[1000005];
ll dis[1000005];
priority_queue<pair<ll, int> > qq;

void dijkstra(int st) {
	memset(dis, 0x3f, sizeof(dis));
	memset(vis, 0, sizeof(vis));
	qq.push(make_pair(0ll, st));
	dis[st] = 0;
	while (!qq.empty()) {
		int x = qq.top().second; qq.pop();
		if (vis[x]) continue;
		vis[x] = 1;
		for (int i = head[x]; i; i = pre[i]) {
			int y = to[i];
			if (dis[y] > dis[x] + val[i]) {
				dis[y] = dis[x] + val[i];
				qq.push(make_pair(-dis[y], y));
			}
		}
	}
}

int main() {
	scanf("%d %d %d", &n, &q, &s);
	build(in, 1, 1, n, 0);
	build(out, 1, 1, n, 1);
	for (int i = 1; i <= n; i++) {
		addedge(pos[0][i], pos[1][i], 0);
		addedge(pos[1][i], pos[0][i], 0);
	}
	for (int i = 1; i <= q; i++) {
		int t, u, x, y; ll w;
		scanf("%d", &t);
		if (t == 1) {
			scanf("%d %d %lld", &x, &y, &w);
			addedge(pos[0][x], pos[1][y], w);
		} else if (t == 2) {
			scanf("%d %d %d %lld", &u, &x, &y, &w);
			query(in, 1, x, y, pos[0][u], w, 0);
		} else {
			scanf("%d %d %d %lld", &u, &x, &y, &w);
			query(out, 1, x, y, pos[1][u], w, 1);
		}
	}
	ll inf = 0x3f3f3f3f3f3f3f3f;
	dijkstra(pos[0][s]);
	for (int i = 1; i <= n; i++) {
		printf("%lld ", dis[pos[1][i]] == inf ? -1 : dis[pos[1][i]]);	
	}
	return 0;
}