Snuketoon [ABC217H]

https://atcoder.jp/contests/abc217/tasks/abc217_h

题解

设 $f_{i,x}$ 表示在 $T_i$ 时刻在 $x$ 位置，受到的最小伤害是多少

记 $m_i = T_i-T_{i-1}$

以 $D_i=0$ 为例，转移有 $f_{i,x}=\min\limits_{y\in [x-m_i,x+m_i]} f_{i-1,y} + \min\{X_i-x,0\}$

观察一下样例可以发现，对于一个固定的 $i$ ，若把所有 $(x,f_{i,x})$ 当成点画在二维平面上并连接相邻点，那么图像会是一段下凸壳，也就是说 $f_{i,x}$ 是一个下凸的函数

不妨把上面的转移分成两步，先是 $f_{i,x}=\min\limits_{y\in [x-m_i,x+m_i]} f_{i-1,y}$

此时对于凸壳左半边斜率小于 $0$ 的部分，有 $f_{i,x-1} > f_{i,x}$ ，所以 $f_{i,x}=\min\limits_{y\in [x-m_i,x+m_i]} f_{i-1,y}=f_{i-1,x+m_i}$

同理对于右半边斜率大于 $0$ 的部分，有 $f_{i,x}=f_{i-1,x-m_i}$

所以这一步就相当于将凸壳左半边向左平移 $m_i$ ，右半边向右平移 $m_i$

第二步是给每个 $f_{i,x}$ 加上 $\min\{X_i-x,0\}$ (仍然以 $D_i=0$ 为例)

可以发现，这个操作相当于给 $[-\infty,X_i]$ 这段的 $f_{i,x}$ 加上一个斜率为 $-1$ 的一次函数

考虑怎么维护这个凸壳：

对于左半边斜率小于0的部分，从右到左维护若干个断点 $p_1,p_2,\dots,p_k$，表示 $[p_1,p_2]$ 区间上凸壳斜率为 $-1$ ，$[p_2,p_3]$ 上斜率为 $-2$，......

对于右半边同理；额外维护一个 $ans$ 表示斜率为 $0$ 部分的答案

对于第一步转移，直接维护左半边和右半边的偏移量即可

对于第二步转移，以 $D_i=0$ 为例，设右半边凸壳的第一个断点为 $r$

如果 $X_i \le r$ ，那么此时 $X_i$ 左边的部分斜率要全部 $-1$ ，所以将 $X_i$ 作为断点加入左半边凸壳的断点集合即可

如果 $X_i > r$ ，那么有一段原来斜率为 $1$ 的区间加上这个斜率为 $-1$ 的一次函数后斜率变成 $0$ 了，更新 $ans+=X_i-r$，同时将右半边第一个断点改为 $X_i$ ，左半边新增了断点 $r$

下面放一张图方便理解：

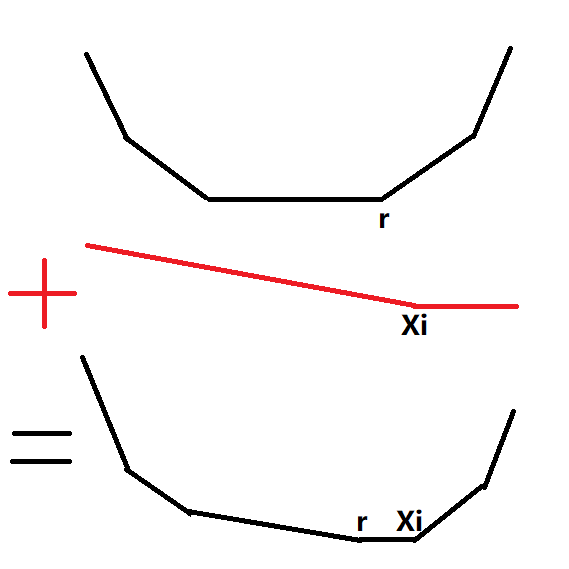
$D_i=1$ 时也同理

最后答案即为 $ans$

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int n;
priority_queue<ll> q0;
priority_queue<ll, vector<ll> , greater<ll> > q1;

int main() {
	scanf("%d", &n); ll ans = 0;
	for (int i = 1, t, d, x; i <= n; i++) {
		scanf("%d %d %d", &t, &d, &x);
		if (d == 0) {
			if (x > t) ans += x-t, x = t;
			if (q1.empty() || x <= q1.top()+t) q0.push(x+t);
			else {
				ll y = q1.top()+t;
				ans += x-y;
				q0.push(y+t); 
				q1.pop(); q1.push(x-t);
			}
		} else {
			if (x < -t) ans += -t-x, x = -t;
			if (q0.empty() || x >= q0.top()-t) q1.push(x-t);
			else {
				ll y = q0.top()-t;
				ans += y-x;
				q0.pop(); q0.push(x+t);
				q1.push(y-t);
			}
		}
	}
	printf("%lld\n", ans);
	return 0;
}