寻找车位[Code+#3]

题目描述

access_globe 有一个巨大的停车场，这个停车场有 \(N\) 行，每行有 \(M\) 个车位。为了美观，access_globe 在建立这个停车场时，规定这个停车场必须是长条形的，即 \(N\ge M\) 。每个车位都是一个正方形的区域。

最近，access_globe 正在为抽不到 Missing Poster 而苦恼，因此他请你帮他维护这个停车场。你需要支持两个事件：

• 一辆车停到某一个车位中，或一辆车从某个车位开走
• 查询一个矩形区域内最大的只包含空车位的正方形区域

如果你能帮 access_globe 高效地解决这个问题，access_globe 一定会好好奖励你的。

\(N \times M \le 4*10^6,Q\le 2000\)

题解

线段树神题

对 \(N\) 这一维开一棵线段树，然后线段树上的每个节点维护3个数组：lm[M], rm[M], val[M]

假设线段树的某个节点表示的是 \([l,r]\) 这段区间 (\(1\le l\le r\le N\)) ，那么这个节点的 lm[i] 表示第 \(i\) 列中，从第 \(l\) 个车位开始往后数有多少个连续的 \(1\) ，rm[i] 表示从第 \(r\) 个车位往前数有多少个连续的 \(1\)

这个节点的 val[i] 表示如果以第 \(i\) 列作为正方形的右边界，且正方形的上下边界在 \([l,r]\) 内 (这里的 \(l,r\) 实际上是竖着的一段区间) ，全1的正方形的边长最大是多少

lm[M] 和 rm[M] 都很容易通过左右儿子的值求出来，如何求出 val[M] ?

假设 \(mid=\dfrac{l+r}{2}\)，先考虑这个正方形的上下边界都在 \([l,mid]\) 或者都在 \([mid+1,r]\)

显然此时 val[i] 等于左右儿子的 val[i] 的较大值

如果正方形跨过了 \(mid\) 呢?

假设我们现在已经知道了正方形的上下边界在 \([l,r]\) 内，如果正方形的右边界在 \(i\)，左边界在 \(j\) (即边长为 \(i-j+1\) ) ，如何判断是否存在合法的正方形？

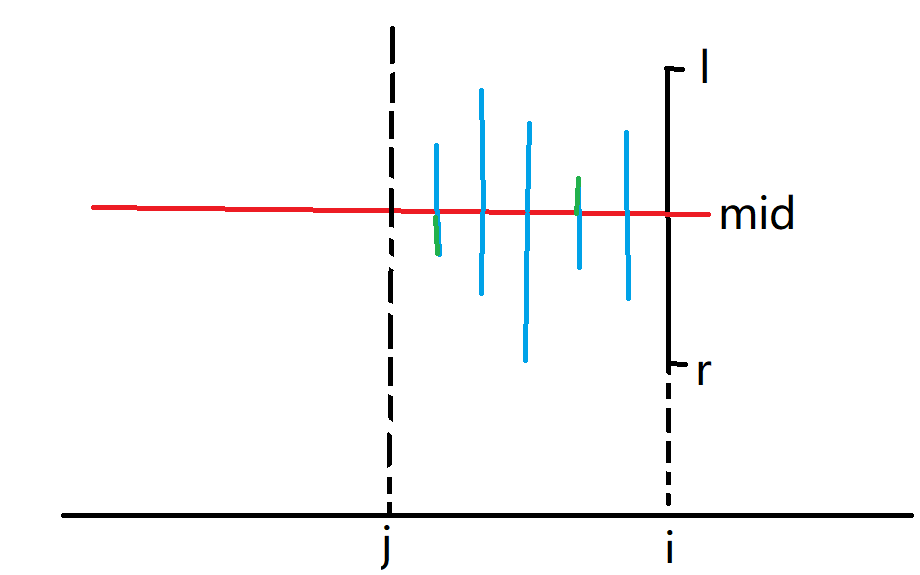
如图 我们对于 \([j,i]\) 中的每一列，找到从第 \(mid\) 行开始有多少个向上延申的连续的 \(1\) (蓝线)，同理找到向下延申的，然后分别找到向上和向下最少的 (绿线) ， 记为 \(a,b\) ，如果 \(i-j+1\le a+b\) ，就表示一定存在合法的正方形

容易发现如果以 \(i\) 为右边界可以构成的最大全1正方形的左边界在 \(j\) ，那么以 \(i+1\) 为右边界可以构成的最大全1正方形的左边界不可能小于 \(j\)

所以这个每次查询区间 \([j,i]\) 的最小值可以使用单调队列来维护，枚举右端点 \(i\) 并且维护另外一个指针 \(j\) ，如果此时 \(i-j+1\) 大于上下两个最小值之和，那就说明不满足条件，\(j\) 继续右移，找到第一个满足条件的 \(j\) ，那么 \([l,r]\) 这个线段树节点的 val[i] 就等于 \(j\)

这样就通过合并左右儿子两个区间算出了当前节点的值了

注意这样 pushup 一次的复杂度是 \(O(m)\) 的，所以进行一次修改或查询

那么怎么查询答案呢？

假设询问是 \(x1,y1,x2,y2\)，将 \([x1,x2]\) 在线段树上分为 \(\log N\) 个区间，然后在线段树上合并这些区间即可

一种比较聪明的做法是用一个没有用的节点暂时储存一下这 \(\log N\) 个区间合并得到的答案，最后只需要找出这个临时节点 val[y1] 到 val[y2] 之间的最大值即可

代码

#include <bits/stdc++.h>
#define N 4000005
using namespace std;

template <typename T>
inline void read(T &num) {
	T x = 0, f = 1; char ch = getchar();
	for (; ch > '9' || ch < '0'; ch = getchar()) if (ch == '-') f = -1;
	for (; ch <= '9' && ch >= '0'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ '0');
	num = x * f;
}

int n, m, Q;
int len[N<<2], q1[N], q2[N];
vector<int> A[N];
int lm[N<<2], rm[N<<2], val[N<<2];

inline int o(int x, int y) { return x*m+y; } 

inline void merge(int ind, int ls, int rs) {
    int h1 = 1, h2 = 1, t1 = 0, t2 = 0;
    for (int r = 1, l = 1; r <= m; r++) {
        while (h1 <= t1 && rm[o(ls,q1[t1])] > rm[o(ls,r)]) t1--;
        q1[++t1] = r;
        while (h2 <= t2 && lm[o(rs,q2[t2])] > lm[o(rs,r)]) t2--;
        q2[++t2] = r;
        while (h1 <= t1 && h2 <= t2 && rm[o(ls,q1[h1])] + lm[o(rs,q2[h2])] < r-l+1) {
            if (q1[h1] == l) h1++;
            if (q2[h2] == l) h2++;
            l++;
        }
        val[o(ind,r)] = max(max(val[o(ls,r)], val[o(rs,r)]), r-l+1);
    }
    for (int i = 1; i <= m; i++) lm[o(ind,i)] = lm[o(ls,i)] + (lm[o(ls,i)]==len[ls]?lm[o(rs,i)]:0);
    for (int i = 1; i <= m; i++) rm[o(ind,i)] = rm[o(rs,i)] + (rm[o(rs,i)]==len[rs]?rm[o(ls,i)]:0);
}
void build(int ind, int l, int r) {
    len[ind] = r-l+1;
    if (l == r) {
        for (int i = 1; i <= m; i++) lm[o(ind,i)] = rm[o(ind,i)] = val[o(ind,i)] = A[l][i];
        return; 
    }
    int mid = (l + r) >> 1;
    build(ind<<1, l, mid); build(ind<<1|1, mid+1, r);
    merge(ind, ind<<1, ind<<1|1);
}
void update(int ind, int l, int r, int x, int y, int v) {
    if (l == r) {
        lm[o(ind,y)] = rm[o(ind,y)] = val[o(ind,y)] = v;
        return; 
    }
    int mid = (l + r) >> 1;
    if (x <= mid) update(ind<<1, l, mid, x, y, v);
    else update(ind<<1|1, mid+1, r, x, y, v);
    merge(ind, ind<<1, ind<<1|1);
}

void query(int ind, int l, int r, int x, int y) {
    int ret = 0;
    if (x <= l && r <= y) {
        merge(0, 0, ind); //用0号点暂时储存答案
        return;
    }
    int mid = (l + r) >> 1;
    if (x <= mid) query(ind<<1, l, mid, x, y);
    if (mid < y) query(ind<<1|1, mid+1, r, x, y);
}

int main() {
    read(n); read(m); read(Q);
    for (int i = 1; i <= n; i++) A[i].resize(m+1);
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) {
        read(A[i][j]);
    }
    build(1, 1, n);
    for (int i = 1, tp, x, y, a, b; i <= Q; i++) {
        read(tp);
        if (tp == 0) {
            read(x); read(y);
            if (A[x][y]) update(1, 1, n, x, y, 0);
            else update(1, 1, n, x, y, 1);
            A[x][y] = 1 - A[x][y];
        } else {
            read(x); read(y); read(a); read(b);
            for (int j = 1; j <= m; j++) {
                lm[o(0,j)] = rm[o(0,j)] = val[o(0,j)] = 0; //用0号点暂时储存答案
            }
            query(1, 1, n, x, a);
            int ans = 0;
            for (int j = y; j <= b; j++) {
                ans = max(ans, min(j-y+1, val[o(0, j)]));
            }
            printf("%d\n", ans);
        }
    }
    return 0;
}