树的计数[NOI2013]
题目描述
我们知道一棵有根树可以进行深度优先遍历(DFS)以及广度优先遍历(BFS)来生成这棵树的 DFS 序以及 BFS 序。两棵不同的树的 DFS 序有可能相同,并且它们的 BFS 序也有可能相同,例如下面两棵树的 DFS 序都是 1 2 4 5 3,BFS 序都是 1 2 3 4 5。
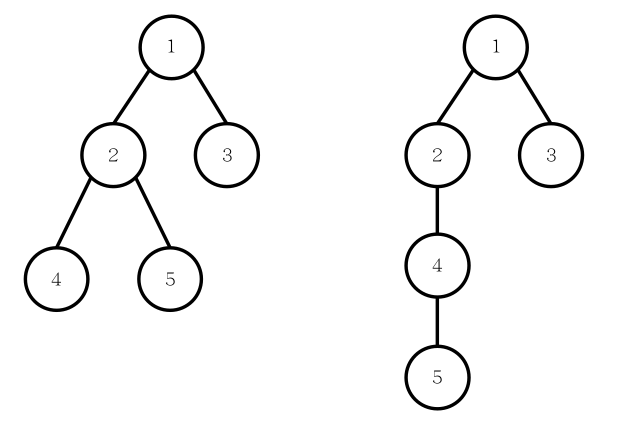
现给定一个 DFS 序和 BFS 序,我们想要知道,符合条件的有根树中,树的高度的平均值。即,假如共有 \(K\) 棵不同的有根树具有这组 DFS 序和 BFS 序,且他们的高度分别是 \(h_1,h_2,\cdots,h_K\),那么请你输出:
输入格式
第一行包含 \(n\) 个正整数 ,表示树的节点个数。
第二行包含 \(n\) 个正整数,是一个 \(1\dots n\) 的排列,表示树的 DFS 序。
第三行包含 \(n\) 个正整数,是一个 \(1\dots n\) 的排列,表示树的 BFS 序。
输入保证至少存在一棵树符合给定的两个序列。
输出格式
输出 \(1\) 个实数,四舍五入保留恰好三位小数,表示树高的平均值。
题解
对于给出的dfs序和bfs序,一定有一种方法给点重新标号,使得bfs序变成 \(1,2,3,\cdots,n\) 这个样子
以样例为例:dfs序为 \(1,2,4,5,3\),bfs序为 \(1,2,3,4,5\)
发现深度相同的点,在bfs序中一定是连续一段的,所以原题目可以看作给bfs序进行分段,使得分段后满足dfs序
样例中 \(n=5\),有4个分段点
经过观察,有如下几个分段的限制条件:
条件一
深度为1的点一定只有一个(根),所以 \(1\) 后面要进行分段。变为 \(1 | 2 3 4 5\)
条件二
设 \(p[i]\) 表示 \(i\) 在dfs序中在第几个,如 \(p[3]=5,p[4]=3\)
对于 \(i \in [1, n)\),如果 \(p[i]>p[i+1]\),那么有如下两种情况:
(以样例 \(p[3]>p[4]\) 为例)
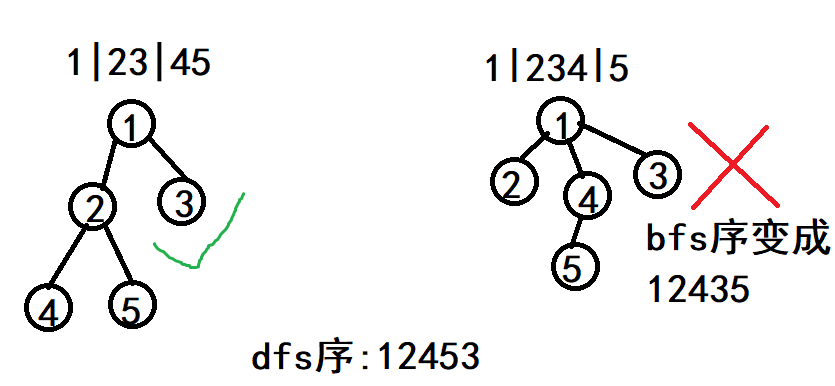
得到限制条件:对于 \(i \in [1, n)\),如果 \(p[i]>p[i+1]\),那么 \(i\) 与 \(i+1\) 之间要分段
样例中,\(3\) 和 \(4\) 之间必须要有分割线,即 \(1|23|45\)
样例中,只有 \(3\) 满足 \(p[i]>p[i+1]\),所以已经确定的必须要有的分割线为 \(1|23|45\)
条件三
dfs序为 \(12453\),\(2\) 后一个为 \(4\),所以点 \(4\) 的深度最多比点 \(2\) 多 \(1\)
在bfs序中,这就等价于说 \(2\) 和 \(4\) 之间最多有一条分割线
形式化地,设dfs序数组为 \(d[N]\),那么对于 \(i\in [1,n)\),如果 \(d[i]+1<d[i+1]\),那么在bfs序中 \(d[i]\) 与 \(d[i+1]\) 之间最多有一条分割线
发现在样例中,\(24\) 连在一起,那么 \(3\) 要不在 \(2\) 前面,要不在 \(4\) 后面
如果 \(3\) 在 \(2\) 前面,那么有 \(p[2]>p[3]\),出现条件二的情况,\(2\) 和 \(3\) 之间必须有分割线
如果 \(3\) 在 \(4\) 后面,那么有 \(p[3]>p[4]\),出现条件二的情况,\(3\) 和 \(4\) 之间必须有分割线
样例中就有 \(p[3]>p[4]\),所以\(3\) 和 \(4\) 之间必须有分割线
所以可以得出结论:\(2\) 和 \(4\) 之间必定至少有一条 由条件二得出的必须存在的分割线
又因为 \(2\) 与 \(4\) 之间最多有一条分割线,所以 \(2\sim 4\) 之间别的未确定的空隙中就必定是没有分割线的
以上就是3个分割条件,然后考虑如何实现
先找出所有的必须存在的分割线(条件一,二)
样例中必须存在的分割线就是 \(1|23|45\)
然后根据条件三,\(2\sim 4\) 之间剩余的空隙就不能填分割线,这里也就是 \(2\) 和 \(3\) 之间的那个空隙一定不能填
我们把所有 必须填/必须不填 的分割点打上标记,而可以自由选择填或不填的就不打标记
对于条件一,二,有必须要填的分割线,把必须要填的地方打上标记,并且让答案+1(必须多分割出一层)
对于条件三,有必须不填的分割线,把必须不填的地方打上差分标记
然后扫一遍,如果有可以自由选择填或不填的分割点,就让答案加上0.5
#include <bits/stdc++.h>
#define N 200005
using namespace std;
typedef long long ll;
template <typename T>
inline void read(T &num) {
T x = 0, f = 1; char ch = getchar();
for (; ch > '9' || ch < '0'; ch = getchar()) if (ch == '-') f = -1;
for (; ch <= '9' && ch >= '0'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ '0');
num = x * f;
}
int n, a[N], b[N], sum[N];
double ans;
int main() {
read(n); ans = 2;
for (int i = 1; i <= n; i++) read(a[i]);
for (int i = 1, x; i <= n; i++) {
read(x); b[x] = i;
}
for (int i = 1; i <= n; i++) {
a[i] = b[a[i]];
}
for (int i = 1; i <= n; i++) {
b[a[i]] = i;
}
sum[1]++; sum[2]--; //ban:1
for (int i = 1; i < n; i++) {
if (b[i] > b[i+1]) {
//情况1:i后面必须分段
ans++;
sum[i]++; sum[i+1]--; //ban:i
}
}
for (int i = 1; i < n; i++) {
if (a[i] + 1 < a[i+1]) {
//a[i]~a[i+1]只能分一次段, 且肯定至少有一个情况1
//若有大于等于两个情况1则无解
sum[a[i]]++; sum[a[i+1]]--; //ban:a[i]~a[i+1]-1
}
}
int now = 0;
for (int i = 1; i < n; i++) {
now += sum[i]; //差分
if (!now) ans += 0.5; //now==0表示可以自由选择在i后面分割
}
printf("%.3lf\n", ans);
return 0;
}


