通信原理期末复习笔记

第一章 绪论
通信性能指标:
信息量:消息x所含的信息量I是x发生的概率的函数 \(I(x)=-\log_2(P(x))\) 单位 bit
信息传输速率:
-
传码率\(R_B\):单位时间内传输码元(可以是二进制、多进制)的个数,单位 Baud/s
-
传信率\(R_b\):单位时间内传输的比特总数,单位 bit/s或bps
-
关系:\(R_b =R_B \log_2M\) 其中 M 为进制数
频带利用率(2种表示方式,B为信号传输占用的带宽):
- \(\eta=\frac{R_B}{B} ~~(Baud/Hz)\)
- \(\eta_b=\frac{R_b}{B} ~~(bit/s/Hz)\)
误码率:
- 码元差错率:\(P_e=\frac{错误码元数}{传输的总码元数}\)
- 信息差错率:\(P_e=\frac{错误比特数}{传输的总比特数}\)
第二章 随机信号与噪声分析
随机过程X(t)的数字特征
-
数学期望:\(E[X(t)]=\int_{-\infty}^{+\infty}x f(x, t)dx\)
-
方差:\(D[X(t)] = E\{[X(t)-a(t)]^2\}\) 其中a(t)为数学期望
-
自相关函数(重要):\(R(t_1, t_2)=E[X(t_1)X(t_2)]\)
-
协方差函数:\(B(t_1, t_2)=E\{[X(t_1)-a(t_1)][X(t_2)-a(t_2)]\}\),
且 \(B(t_1, t_2)=R(t_1, t_2)-a(t_1)a(t_2)\) (重要)
平稳随机过程
广义平稳:
- 均值与时间t无关,为常数\(a\)
- 自相关函数只与时间间隔有关,为\(R(\tau)\)
狭义平稳:
- 一维情况:的概率密度函数与时间t无关
判断 \(X(t)=A\cos(\omega t+φ)\) 的平稳性,其中A和ω为常数,φ服从【均匀分布】,则
- \(E[X(t)]=0\)
- \(R_X(t_1,t_2)=\frac{A^2}{2}\cos\omega \tau\),其中 \(\tau=t_2-t_1\)
综上:X(t)是广义平稳的
【平稳随机过程的各态历经性】:
假设 x(t) 是平稳随机过程 \(X(t)\) 的任意一次实现,则其时间均值、时间相关函数分别为:
- 时间均值:\(\overline{a}=\lim_{T\to\infty}\frac{1}{T}\int_{-T/2}^{T/2} x(t)dt\)
- 时间相关函数:\(\overline{R(\tau)}= \lim_{T \to \infty} \frac{1}{T} \int_{-T/2}^{T/2} x(t)x(t+\tau)dt\)
如果平稳过程使得下式成立:
- \(a=E[X(t)]=\overline{a}\)
- \(R(\tau)=\overline{R(\tau)}\)
则该平稳随机过程具有各态历经性
【自相关函数的性质】:
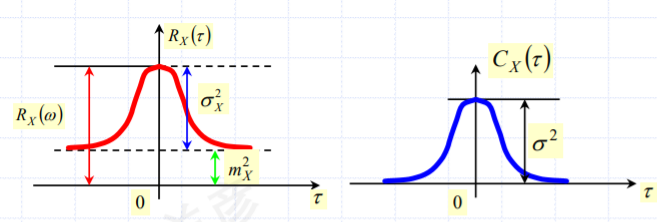
记住这幅图就可以记住 \(R(\tau)\) 的性质(拿随机信号处理的PPT的图来顶一下😅)
- \(R(\tau)\) 为偶函数
- \(R(0)=E[X^2(t)]=\sigma^2 + E^2(\infty)\) 图中的 \(\sigma_X^2\) 即方差, \(m_X^2\) 即 \(E^2(\infty)\)
- \(R(0)\)为平均功率, \(\sigma^2\)为交流功率, \(E^2(\infty)\) 为直流功率
【功率谱密度函数\(P_X(\omega)\)】
-
确定信号:\(P_x(\omega)=\lim_{T\to \infty} \frac{|X_T(\omega)|^2}{T}\)
-
随机信号:\(P_X(\omega)= E[P_x(\omega)] = \lim_{T\to \infty} \frac{E[|X_T(\omega)|^2]}{T}\)
性质:自相关函数的傅里叶变换等于 \(P_X(\omega)\),即 \(R(\tau)\Leftrightarrow P_X(\omega)\)
-
\(P_X(\omega)\) 是确定函数,偶函数,非负函数
-
随机过程的平均功率=\(R(0)=\frac{1}{2\pi}\int_{-\infty}^{+\infty} P_X(\omega) d\omega\)
第三章 信道与噪声
香农公式:
信道容量:\(C=B\log_2(1+S/N)\) (bit/s)
第四章 模拟调制系统
幅度调制
-
普通调幅AM
\(s_{AM}(t)=[A_0+m(t)]\cos \omega_ct\) 其中m(t)为输入的调制信号,输出\(s_{AM}(t)\) 为【调幅信号】,所以经过调制的信号都可称为 【已调信号】
调幅度:\(\frac{\max(m(t))}{A_0}\) 调幅度小于等于 1 时可以采用包络检波
-
双边带调幅DSB
\(s_{DSB}=m(t)\cdot \cos(\omega_ct)\)
-
单边带调制(调制结果分为上边带、下边带两种)
-
上边带:\(s_{USB}=\frac{1}{2}m(t)\cos(\omega_ct)-\frac{1}{2}\hat{m}(t)\sin(\omega_ct)\)
-
下边带:\(s_{LSB}=\frac{1}{2}m(t)\cos(\omega_ct)+\frac{1}{2}\hat{m}(t)\sin(\omega_ct)\)
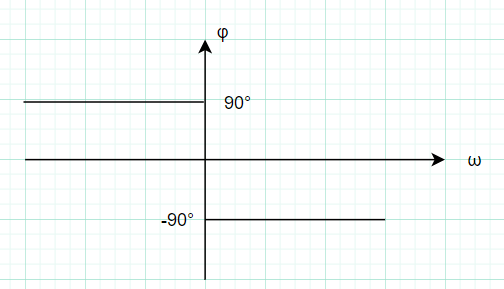
注:\(\hat{m}(t)\) 是 \(m(t)\) 的希尔伯特变换,即 m(t) 的正频率部分相位减去 \(\frac{\pi}{2}\)
-
带宽:\(B_{AM}=B_{DSB}=2B_{SSB}=2B_{VSB}\)
功率:设 \(P_m\)为调制信号 \(m(t)\) 的平均功率\(E(m^2(t))\),则
- \(P_{AM}=载波功率+边带功率=P_c+P_s=\frac{A_0^2}{2}+\frac{P_m}{2}\)
- \(P_{DSB}=P_s=\frac{P_m}{2}\)
- \(P_{SSB}=\frac{1}{2}P_s=\frac{1}{4}P_m\)
调制效率:\({\Large \eta_{AM}=\frac{P_s}{P_{AM}}}\)
解调:
-
AM解调:
- 相干解调:\(m_o(t)\approx \frac{1}{2}[m(t)+A_0]\overset{隔直}{\rightarrow} \frac{1}{2}m(t)\)
- 包络检波:\(m_o(t)\approx m(t)+A_0\overset{隔直}{\rightarrow} m(t)\)
-
DSB解调:
相干:\(m_o(t)=\frac{1}{2}m(t)\) 输出功率:\(P_o=\frac{1}{4}\overline{m^2(t)}=\frac{1}{4}P_m\)
-
SSB解调:
相干:\(m_o(t)=\frac{1}{4}m(t)\), \(P_o=\frac{1}{16}\overline{m^2(t)}=\frac{1}{16}P_m\)
解调器的信噪比增益:
- \(G_{AM}\le 1\) (包络检波、且为大信噪比时),单音调制,且调制度=100%时,\(G_{AM}=2/3\)
- \(G_{DSB}=2\)
- \(G_{SSB}=1\)
平稳高斯白噪声 \(n_i(t)\) 通过解调器后,输出 \(n_o(t)=n_i(t)/2\),因此输出噪声功率 \(N_o=N_i/4\)
通常高斯白噪声的[双边]功率谱 \(\frac{n_0}{2}\) W/Hz,[单边]功率谱为 \(n_0\) W/Hz
角度调制
调角信号:\(s_{m}(t)=A_0\cos(\omega_ct+\varphi(t))\)
- 调相:\(\varphi(t)=K_P m(t)\)
- 调频:\(\frac{d\varphi(t)}{dt}=K_F m(t)\)
调频带宽:\(B_{FM}=2(D+1)f_m\) ,其中 \(f_m\) 为调制信号m(t)的最高频率
- 窄带调频时,\(D<<1, B_{NBFM}=2f_m\)
- 宽带调频时,\(B_{FM}=2(D+1)f_m\)
- D为调频指数,\(D=\Delta f_m/f_m\), \(\Delta f_m=K_F|m(t)|_{\max}\) 为最大频偏,单音调制时用 \(m_f\)代替 D
功率:窄带、宽带均为 \(P_{FM}=载波功率=A_0^2/2\)
调频信号的解调:
- 非相干解调 \(m_o(t)=K_dK_Fm(t)\)
- 相干解调:\(m_o(t)=\frac{1}{2}A_0K_Fm(t)\)
信噪比增益:\(G_{FM}=3m_f^2(m_f+1)\approx 3m_f^3\)
第五章 数字基带传输系统
各种编码
-
单极性不归零码
-
双极性不归零码
-
单极性归零码
-
双极性归零码
-
AMI码(传号反转码,1码交替用正、负电平表示,0码用低电平表示)
-
HDB3码(解决AMI码中连0长串问题)
原码->AMI码->加V(交替正负)->加B(与后一个V正负相同)->±V、±B改为±1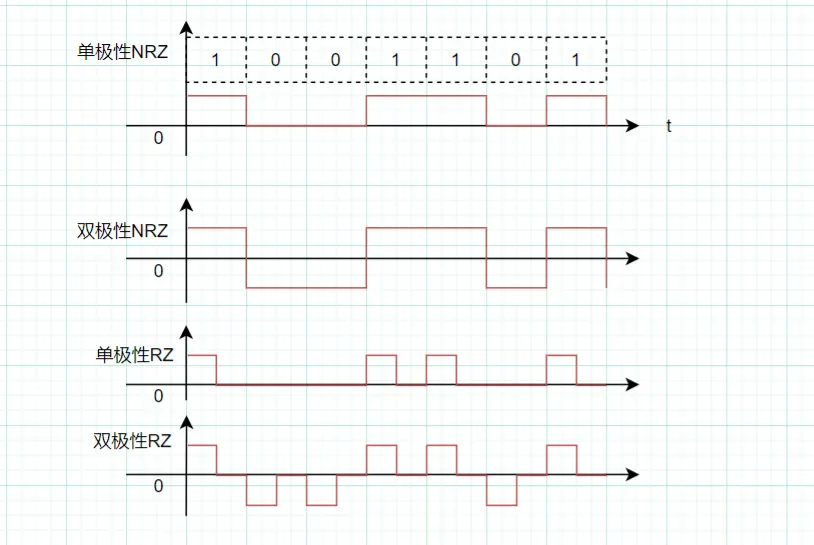
数字基带传输
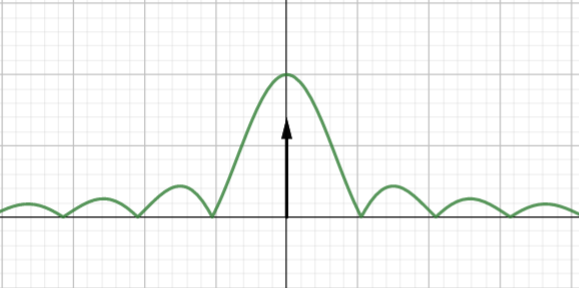
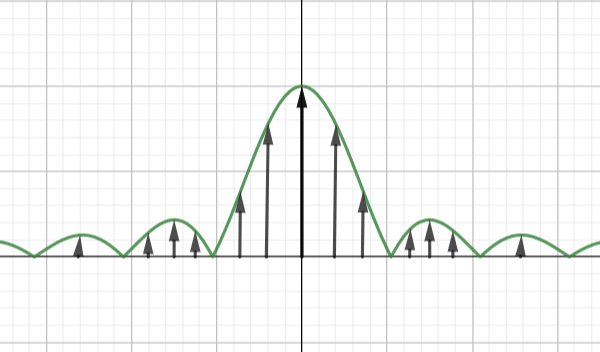
数字基带信号功率谱:
| 单极性NRZ(含直流分量) | 双极性NRZ(0,1等概发送) | 单极性RZ(含离散分量) | 双极性RZ(0,1等概发送) |
|---|---|---|---|
 |
 |
 |
 |
无码间干扰
无码间干扰最大速率:\(R_B=\frac{2}{1+\alpha}f_{ch}\) ,\(f_{ch}\)为系统最高截止频率
最大码速时的频带利用率:\(\eta=\frac{2}{1+\alpha}\) (Baud/Hz)
无码间干扰的误码率:
- 双极性、等概率发送0,1:\(P_e=\frac{1}{2}erfc(\frac{A}{\sqrt{2}\sigma_n})\)
- 单极性、等概率发送0,1:\(P_e=\frac{1}{2}erfc(\frac{A}{2\sqrt{2}\sigma_n})\)
部分响应系统
特点:频带利用率可以达到 2 Baud/Hz
实现方式:
- 预编码:\(b_k=a_k\oplus b_{k-1}\)
- 相关编码(消除误码传播):\(c_k=b_k+b_{k-1}\)
- 译码:\(a_k=b_k\oplus b_{k-1}=[c_k]_{\mod{2}}\)
均衡器
输出:
第六章 数字信号频带传输
主要介绍如何将数字信号调制到高频范围进行传输
带宽
- \(B_{2ASK}=2R_B\)
- \(B_{2FSK}=|f_1-f_2|+2R_B\)
- \(B_{2DPSK}=B_{2PSK}=2R_B\)
误码率
相干解调
- 2ASK: \(\frac{1}{2}erfc(\sqrt{\frac{r}{4}})\), r>>1时,\(\frac{1}{\sqrt{\pi r}} e^{-r/4}\)
- 2FSK: \(\frac{1}{2} erfc(\sqrt{\frac{r}{2}})\), r>>1时,\(\frac{1}{\sqrt{2\pi r}} e^{-r/2}\)
- 2PSK: \(\frac{1}{2}erfc(\sqrt{r})\), r>>1时,\(\frac{1}{2\sqrt{\pi r}} e^{-r}\)
- 2DPSK: \(erfc(\sqrt{r})\), r>>1时,\(\frac{1}{\sqrt{\pi r}} e^{-r}\)
- 4PSK: \(erfc(\sqrt{r}\sin\frac{\pi}{4})\)
- 4DPSK: \(erfc(\sqrt{2r}\sin\frac{\pi}{8})\)
非相干解调
- 2DPSK(差分相干解调): \(\frac{1}{2}e^{-r}\)
- 2FSK(包络检波): \(\frac{1}{2}e^{-r/2}\)
- 2ASK(包络检波): \(\frac{1}{2}e^{-r/4}\)
解调框图
......
第七章 现代数字调制技术
主要看书,了解基本目的和原理
QAM:带宽、频率利用率记一下即可
第八章 模拟信号的数字传输
主要介绍模拟信号如何转换为数字信号:采样、量化、编码
采样定理
\(f_s=2f_m\)
了解一下理想采样、自然采样、平顶采样
带通抽样定理
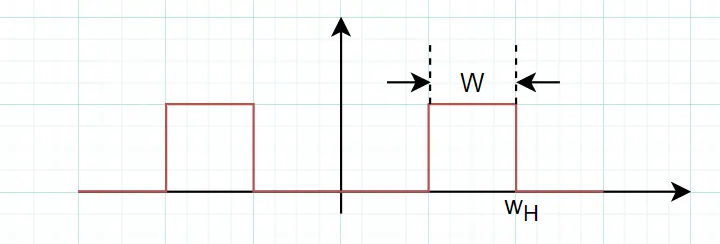
采样角频率:
其中
- \(N= floor(\omega_H/W)\),也就是 \(\omega_H/W\)的整数部分
- \(M=\frac{\omega_H}{W}-N\), 且 \(0\le M < 1\)
最终 \(2W<\omega_s<4W\)
量化
均匀量化:
- 最小量化间隔:\(\Delta A=\frac{b-a}{M}\),最大值b,最小值a,M个量化区间
- 最大量化误差:\((\Delta q)_{\max}=\Delta A/2\)
- 量化信噪比:\(\frac{S_o}{N_o}=M^2\)
非均匀量化:
A律压缩曲线:
采用13折线编码:A=87.6
量化信噪比:
- 大信噪比时:\(\frac{S_o}{N_o}=2^{2N_b},N_b\ge \log_2M\)
- 小信噪比时:\(\frac{S_o}{N_o}=\frac{1}{4P_e}\), Pe为误码率
PCM编码
十三折线编码基本步骤
例题:对抽样值1268进行量化编码
编码结果是一个8位码 \(b_7b_6b_5b_4b_3b_2b_1b_0\)
-
符号位 \(b_7\):1-正,0-负;1268为正数,则\(b_7=1\)
-
段落码 \(b_6b_5b_4\):根据下表判断该取哪个值,比如,抽样值为567,则\(512\le567<1024\),则\(b_6b_5b_4=110\)。抽样值为1268>1024,则\(b_6b_5b_4=111\)
抽样值 \(b_6b_5b_4\) 1024 111 512 110 256 101 128 100 64 011 32 010 16 001 0 000 -
段内码 \(b_3b_2b_1b_0\):将对应区间分成均匀分为16份,比如抽样值为567,所在区间为[512, 1024),分成16份,每份大小为(1024-512)/16=32;题中给的抽样值 1268>1024,因此1268所在的区间为[1024, 2048),每份大小ΔA=(2048-1024)/16=64,则
0000对应
10240001对应
1024+64*10010对应
1024+64*2,...
1111对应
1024+64*15 -
因为
1024+64*3=1216< 1268 <1024+64*4=1280,因此1268对应的 \(b_3b_2b_1b_0=0011\) -
综上,得到最终编码为 11110011
-
误差计算
- 采用起始电平为译码电平时,则实际上11110011对应1216,因此 误差=1268-1216=52
- 通常采用中间电平为译码电平,即在原来的基础上加 ΔA/2,则1110011对应译码后应该为 1216+64/2=1248,因此最终【误差】=1268-1248=20
时分复用TDM
- \(f_s=2f_m\), \(T_s=\frac{1}{2f_m}\)
- 每个0、1信号占用时间:\(T_b=\frac{T_s}{N_b n}\), n代表几路信号进行复用
- \(R_B=1/T_b\)
- 无码间干扰带宽:\(B=R_B/2\)
- 主瓣带宽:\(B=1/\tau\),τ表示码元宽度
不采用时分复用时:\(R_B=N_bf_s\)
第九章 差错控制编码
基本概念
码重:一个码中1的个数,如0011码重为2
对2个码求异或的结果中1的个数,即码距\(d_0\),如 0011+1000=1011,码距为3
检错与纠错的条件
- \(d_0\ge e+1\),可以检错e个码
- \(d_0\ge 2t+1\),可以纠错t个码
- \(d_0\ge t+e+1且e\ge t\),可以检查出e个错,同时纠正其中t个错
线性分组码
对于一个(n, k)码,即n个码中有k个是信息码,r=n-k个监督码
-
其编码效率为 \(k/n\)
-
监督矩阵 \(H_0=[P~~~I_r]\),其中 \(I_r\)代表单位矩阵,阶数为r,H0共n列,r行。(注:H0是典型化的矩阵,不是典型化需要进行【矩阵初等变化】,才能得到典型化的矩阵)
-
生成矩阵 \(G_0=[I_k~~~P^T]\),其中 \(I_k\)代表单位矩阵,阶数为k,G0共n列,k行。(注:G0是典型化的矩阵,不是典型化需要进行【矩阵初等变化】,才能得到典型化的矩阵)
发送时使用的码组(系统码):\(A=[a_{n-1}a_{n-2}\cdots a_{n-k}]\times G_0\)
【译码方式】
计算校正子 \(S^T=HR^T\),\(R^T\)为接收码组的列向量
\(|S^T|-1=j\),则 R 中从又往左数(0开始)第j个码发生错误,记得在回答时纠正过来
循环码
生成多项式 g(x) 的确定
- g(x)最高次项为 \(x^{n-k}\),常数项为1
- 一般题目会给出许用码组,在许用的码组中找出一个码字,其中 \(a_{n-k}\)左边的码均为0,第n-k个码\(a_{n-k}\)为1,最右边的码\(a_0\)为1,然后根据这个码的\(a_1,a_2,\cdots,a_{n-k-1}\)来判断\(g_1,g_2,\cdots,g_{n-k-1}\)是多少。
证明g(x)是循环码(n,k)的生成多项式
- 即证 \(x^n-1\) 能被 \(g(x)\) 整除
求码多项式A(x)
-
先求监督多项式 \(r(x)\equiv x^{n-k}m(x),模g(x)\)
-
则 \(A(x)=m(x)x^{n-k} + r(x)\)
m(x)为信息码多项式
判断接收到的码多项式 \(R(x)\) 是不是码多项式
- 利用所有码多项式均能被 g(x) 整除的性质
译码:\(S^T=HR^T\) 或 \(S=RH^T\)
第十章 数字信号的最佳接收
最大信噪比准则与匹配滤波器

- 输出噪声功率谱 \(P_{no}(\omega)=\frac{n_o}{2}|H(\omega)|^2\), \(n_0/2\)是输入高斯白噪声的功率谱密度函数\(P_{ni}\)
- 输出噪声总功率 \(N_o=\frac{1}{2\pi}\int_{-\infty}^{+\infty}P_{no}(\omega)d\omega\)
- 输入信号功率 \(E_i=\frac{1}{2\pi}\int_{-\infty}^{+\infty}|S_i(\omega)|^2d\omega\)
- 最大输出信噪比 \(r_{omax}=\frac{E_i}{n_0/2}\)
根据 \(s_i(t)\) 计算匹配滤波器系统函数和冲击响应函数
- \(h(t)=Ks_i(t_0-t)\),通常取 \(K=1, t_0=T_b\)
- \(H(\omega)=KS_i^*(\omega)e^{-j\omega t_0}\)
输出信号计算: \(s_o(t)=KR_{s_i}(t_0-t)\)
匹配滤波器结构
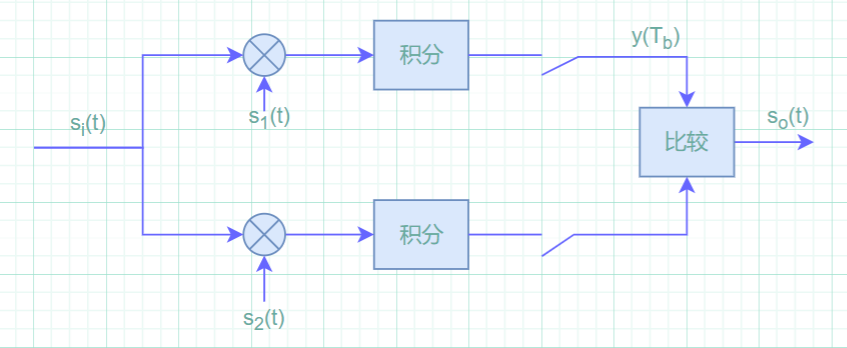
最小误码率准则与相关接收机
判决准则
\(P(s_1)P(x|s_1)>P(s_2)P(x|s_2)\) 则判断为s1, 否则为s2,相等时无法判断,误码率最大
相关接收机结构
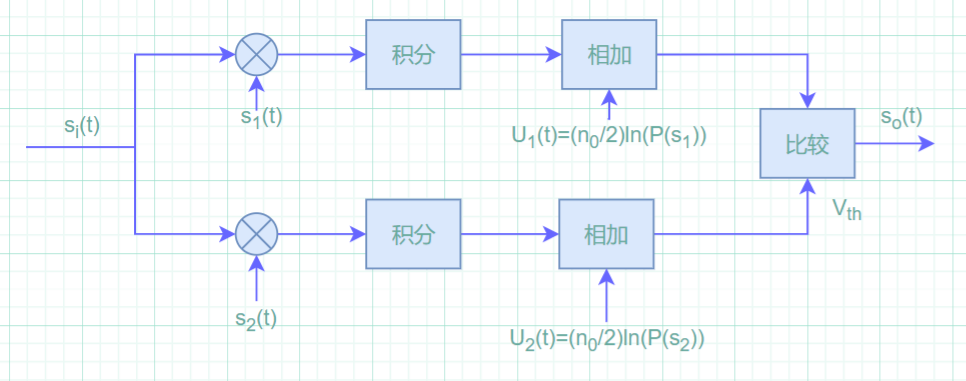
最佳接收机误码率
\(P_e=\frac{1}{2}erfc(\sqrt{\frac{E_b(1-\rho)}{2n_0}})\)
其中,两个信号平均能量\(E_b=\frac{1}{2}\int_{0}^{T}(s_1^2(t)+s_2^2(t))dt\)
相关系数 \(\rho=\frac{\int_0^Ts_1(t)s_2(t)dt}{E_b}\)
- 当使用 双极性码,PSK发送时,ρ=-1
- 当使用 单极性码,ASK或FSK发送时,ρ=0
- ρ=1时,Pe=0.5,误码率最大
第十一章 同步原理
载波同步
- 插入导频法
- 直接提取法
- 平方变换法(平方环法)
- 同相正交环法
位同步
- 外同步法
- NRZ码:在\(\omega_b\)处插入导频
- RZ码,在 \(\omega_b/2\) 处插入导频,然后2倍频即可得到 \(\omega_b\)
- 自同步法
- 模拟锁相环法
- 带限整流法
- 数字锁相环
帧同步
巴克码作帧同步码
本文来自博客园,作者:aJream,转载请记得标明出处:https://www.cnblogs.com/ajream/p/16413202.html

 本科最后一门考试——通信原理复习
本科最后一门考试——通信原理复习

 浙公网安备 33010602011771号
浙公网安备 33010602011771号