10-误差反向传播法（一）——计算图

误差反向传播法

上一篇文章介绍的是用数值微分法计算梯度，但这种方法比较耗时间，接下来介绍新的梯度计算法：误差反向传播法。在此之前，先介绍计算图。

一、计算图

计算图用节点和箭头表示，节点表示某种运算（可以是加减乘除等简单计算，也可以是一个复合运算），箭头上是某些参与计算的数据。

计算图分为正向传播和反向传播，下面这幅图，白色箭头是正向的，蓝色箭头是反向的。

局部计算

每个节点的计算只与当前节点及它的数据有关，各个节点的计算互不干扰。

链式法则

计算图的反向传播：

假设存在 y = f(x)的计算，这个计算的反向传播如图所示。

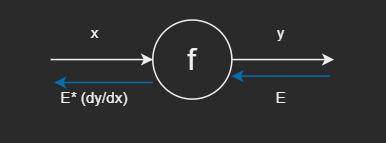
反向传播的计算顺序是，将信号E乘以节点的局部导数 （$\frac{dy}{dx}$），然后将结果传递给下一个节点。这里所说的局部导数是指正向传播 中y = f(x)的导数，即y关于x的导数（$\frac{dy}{dx}$）

通过这样的计算，可以高效地求出导数的 值，这是反向传播的要点

什么是链式法则：

介绍链式法则时，我们需要先从复合函数说起。复合函数是由多个函数 构成的函数。比如，$z=(x+y{)}^2$是由式$\{\begin{array}{l}z=t^2\\ t=x+y\end{array}$的两个式子构成的。

链式法则的原理：如果某个函数由复合函数表示，则该复合函数的导数可以用构成复 合函数的各个函数的导数的乘积表示。用公式表示为：
$$\frac{\partial z}{\partial x}=\frac{\partial z}{\partial t}\frac{\partial t}{\partial x}$$

链式法则和计算图:

以该函数为例：$\{\begin{array}{l}z=t^2\\ t=x+y\end{array}$

其中 a, b, c, d 各字母表示的式子如下：
$$\begin{gathered} d:\frac{\partial z}{\partial z} \\ c:\frac{\partial z}{\partial z}\times \frac{\partial z}{\partial t} \\ b:\frac{\partial z}{\partial z}\times \frac{\partial z}{\partial t}\times \frac{\partial t}{\partial y} \\ a:\frac{\partial z}{\partial z}\times \frac{\partial z}{\partial t}\times \frac{\partial t}{\partial x} \end{gathered}$$

加法节点的反向传播

例：$z=x+y$

$$\begin{gathered} c:\frac{\partial L}{\partial z} \\ b:\frac{\partial L}{\partial z}\times 1 \\ a:\frac{\partial L}{\partial z}\times 1 \end{gathered}$$
可以看到a, b, c 都是一样的，因此，加法节点的反向传播将上游的值原封不动地输出到下游，下面用具体数据来表示，看下面的图，你会对 原封不动 有更深的印象：

乘法节点的反向传播

以 $z=xy$ 为例：

$$\begin{gathered} c:\frac{\partial L}{\partial z} \\ b:\frac{\partial L}{\partial z}\times x \\ a:\frac{\partial L}{\partial z}\times y \end{gathered}$$
乘法的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值” 后传递给下游。

如上图所示，正向传播时信号是x的话，反向传播时则是y（即$\frac{\partial L}{\partial z}\times y$）；正向传播时信号是y的话，反向传播时则是x（即$\frac{\partial L}{\partial z}\times x$）。

下面用具体数据表示，好好理解下什么是翻转：