[学习笔记]普通平衡树(Splay)
好家伙今天心血来潮再次学习了Splay。。。也算是填坑吧,把几年前的坑给填上。
首先,贴题目,洛谷的普通平衡树模板,之前用treap和fhq treap实现过(不过也是快忘完了就是)
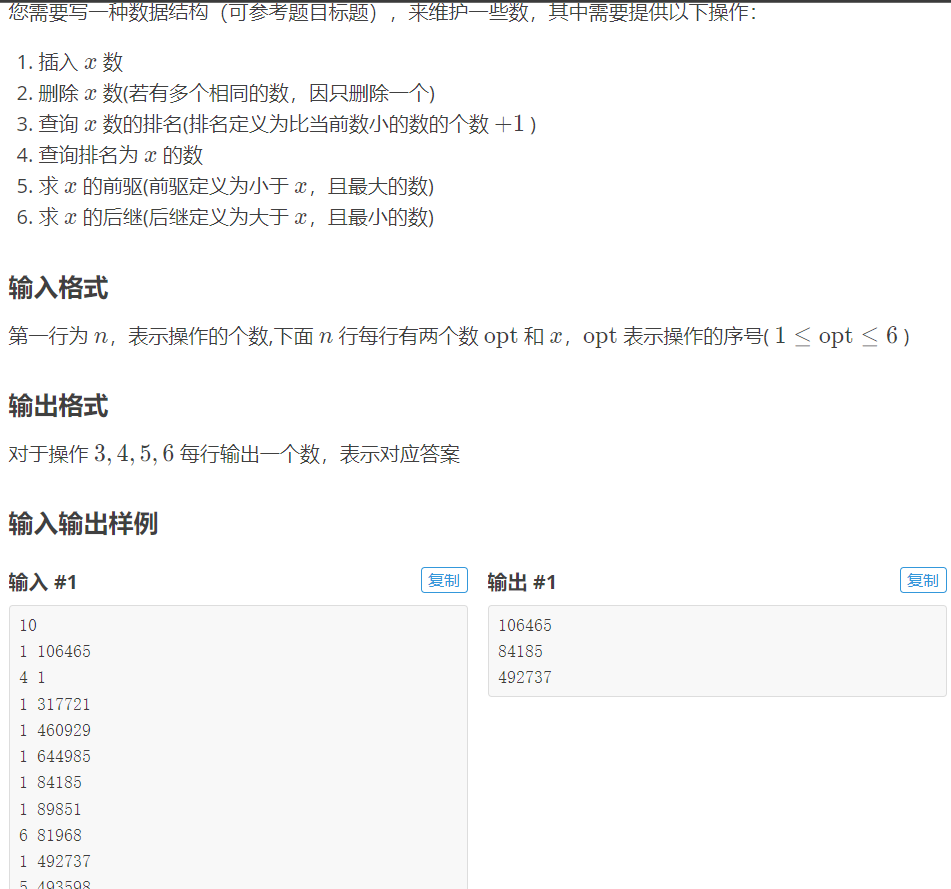
就是要写一个平衡树嘛,平衡树,就是一个平衡的树(废话)
就是一个左右两边差不多大的BST,以保证时间复杂度为O(nlogn)
与treap以时间戳为key值进行的随机不同,Splay是用操作来进行随机化,即利用操作的随机性来不停旋转,以破坏极端的链装情况。
需要注意的是,Splay其实不是一个严格平衡的平衡树,而是均摊时间复杂度为O(nlogn)的平衡树。
Splay中,最核心的操作也是旋转。
因为BST的性质,左子树<节点<右子树
要维护这个性质,需要这样
考虑以下结构,要把A和B的父子关系互换
其中,AB是节点,123是子树。单独考虑子树2(因为它比较特殊,1&3都不需要改变,但2却...),它满足这样的条件:
2的值大于B,小于A
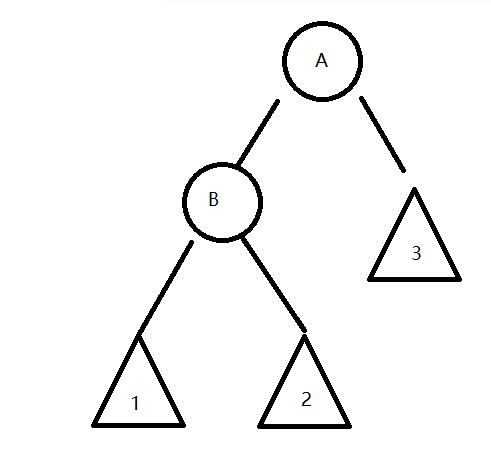
旋转之后,它将变成这样
可以看到,2的位置也发生了改变。这样描述
2的位置从原来的2的值大于B小于A变成了小于A大于B
很形象是不是[doge]
实现代码如下
void rotate(int x) //对一个节点进行旋转 { int y = t[x].f; // x的父节点 int z = t[y].f; // x的爷节点 int k = (t[y].ch[1] == x); //判断是左儿子还是右儿子(这个运算是真的很妙) t[z].ch[(t[z].ch[1] == y)] = x; //把y的位置换成x t[x].f = z; //改变x的父亲(和y换位,于是原本的爷变成了爹) t[y].ch[k] = t[x].ch[k ^ 1]; //更换那个特殊的子树 t[t[x].ch[k ^ 1]].f = y; //转后原本x的儿子的父亲变成y t[x].ch[k ^ 1] = y; // xy互换 t[y].f = x; //更新y的父亲 update(y); update(x); }
其中,update为维护子树size
void update(int x) { t[x].size = t[t[x].ch[0]].size + t[t[x].ch[1]].size + t[x].cnt; //节点的size等于左子树size+右子树size+自己的权重 }
有了这,理论上我们就可以把任何一个点给转到想要的地方了,现在来考虑Splay操作叭
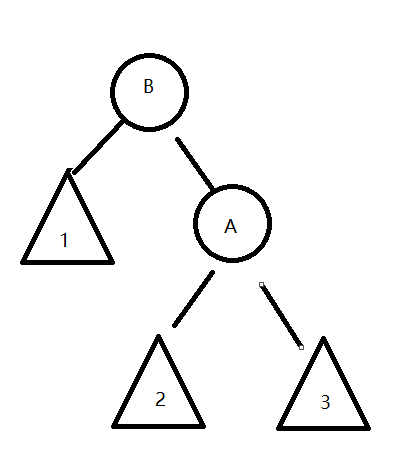
对于极端的情况(比如一条链)
如果只转x,那得到的结果是
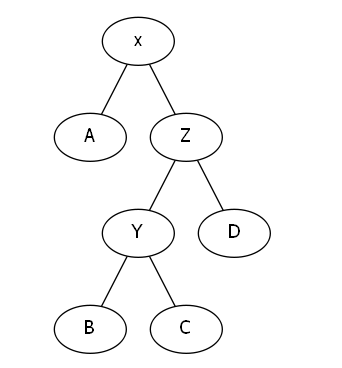
最长链还是四个节点,没有改变。
于是乎,如果是链的情况,我们对于目标节点先转它的父节点。
void splay(int x, int s) //把x转成s的儿子 { while (t[x].f != s) //直到x的f不是s { int y = t[x].f, z = t[y].f; if (z != s) //如果不是链 (t[z].ch[0] == y) ^ (t[y].ch[0] == x) ? rotate(x) : rotate(y); //如果是链就先转y,否则先转x(位运算真的很妙) rotate(x); } if (s == 0) root = x; }
好了,这就是整个Splay了。现在来看题的每一个操作叭。直接贴代码,都在注释里。
0、查找一个数
void find(int x) { int u = root; if (!u) //如果根节点不存在 return; //直接润吧 while (t[u].ch[x > t[u].val] && x != t[u].val) u = t[u].ch[x > t[u].val]; //不断地跳 splay(u, 0); //找到之后把节点转到根节点以方便调用和维护随机 }
1、插入
void insert(int x) { int u = root, f = 0; //从根节点开始 while (u && t[u].val != x) //向下找,找到一个u应该在地位置 { f = u; u = t[u].ch[x > t[u].val]; } if (u) //如果u存在 t[u].cnt++; //那就在这个点加一个权重 else //如果没有 { u = ++tot; //新建一个节点 if (f) //如果父节点非根 t[f].ch[x > t[f].val] = u; //那有一个点的ch就是当前点 t[u].ch[0] = t[u].ch[1] = 0; //更新各种信息 t[tot].f = f; t[tot].val = x; t[tot].cnt = 1; t[tot].size = 1; } splay(u, 0); }
2、删除
void Delete(int x) { int last = next(x, 0); //找前驱 int Next = next(x, 1); //和后继 splay(last, 0); //把last转到根节点 splay(Next, last); //把next转到last的右儿子 int del = t[Next].ch[0]; //要删的就是next的左儿子 if (t[del].cnt > 1) //如果权重>1 { t[del].cnt--; //直接权重-1 splay(del, 0); //并且转到根节点 } else t[Next].ch[0] = 0; //否则直接删除节点(感觉根硬盘的数据擦除差不多,直接把索引给删了,从父节点查无此点) }
3、kth
inline int kth(int x) //查找排名为x的数 { int u = root; //当前根节点 if (t[u].size < x) //如果当前树上没有这么多数 return 0; //不存在 while (1) { int y = t[u].ch[0]; //左儿子 if (x > t[y].size + t[u].cnt) //如果排名比左儿子的大小和当前节点的数量要大 { x -= t[y].size + t[u].cnt; //数量减少 u = t[u].ch[1]; //那么当前排名的数一定在右儿子上找 } else //否则的话在当前节点或者左儿子上查找 if (t[y].size >= x) //左儿子的节点数足够 u = y; //在左儿子上继续找 else //否则就是在当前根节点上 return t[u].val; } }
4、排名
利用find函数,找到那个数然后用其左儿子的size+1
5、前驱&后继
int next(int x, int ff) // ff:0前驱,1后继 { find(x); //先找到x int u = root; //这时候,x就是根节点了 if (t[u].val > x && ff) //如果根节点的值不等于x,那它就是前驱||后继 return u; //大就是前驱,如果要找前驱就返回它 if (t[u].val < x && !ff) return u; u = t[u].ch[ff]; //往左或往右 while (t[u].ch[ff ^ 1]) //一直反着跳直到跳不动,就找到了前驱||后继 u = t[u].ch[ff ^ 1]; return u; }
(完)





