P3521 [POI2011]ROT-Tree Rotations（线段树合并）

一句话题意（不用我改了.....）：给一棵n(1≤n≤200000个叶子的二叉树，可以交换每个点的左右子树，要求前序遍历叶子的逆序对最少。

......这题输入很神烦呐。。。

给你一棵二叉树的dfs序（考场上没发现2333），只有叶子结点有值，然后求逆序对大小

在考场上，建树建了好久，然后暴力暴了好久，然后得到了0分的好成绩呢（我真棒）

正解其实也不难想（但是当时不会权值线段树）

题解：

其实很简单，想想：对于一层的逆序对，数量是一定的。也就是说，无论怎么转当前子树，对上一层的逆序对数量是没有影响的。

挺好理解的但是还是上张图吧：

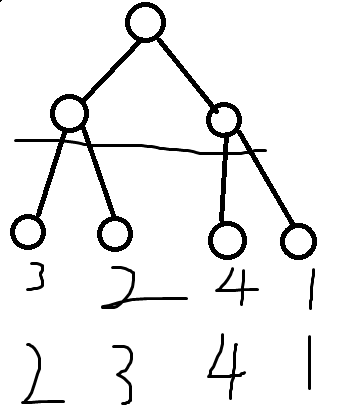
对于第二层来说，无论左边的2,3怎么改变，相对于右边4,1或1,4的逆序对个数始终不会改变。

这个性质吼啊

于是我们只需要求块内的最小逆序对个数就行了。

然后再考虑怎么求逆序对个数。

首先，权值线段树是一个桶，而且下标是有序的（废话）

然后，两课权值线段树在本题中是等价的，也就是说，左右要合并的线段树，除了维护的区间&&存储元素不一样，是满足可并线段树的条件的。

所以，对于一个区间，逆序对只需要比较左区间的右半边（桶中）数量*右区间的左半边就行了，

然后再比较swap之后的，贪心地取下去，合并下去就行了。

.....语言表述有问题，看一下这一小段代码：

ans1+=(ll )t[t[l].rs].sum*t[t[r].ls].sum;
ans2+=(ll )t[t[l].ls].sum*t[t[r].rs].sum;

就这样，比较然后加小的，最后就是总答案了。

tips：真正明白了指针的好处，好好用啊，但是得注意一下，因为指针是直接改值，有些值不能改的话，得用一个中间变量记录。

#include<bits/stdc++.h>
using namespace std;
const int maxn=210000;
#define ll long long
struct tree
{
    int ls,rs,sum;
}t[maxn*30];
ll ans=0,ans1=0,ans2=0;
int n,pos;
int cnt=0;
void insert(int &x,int l,int r)
{
    if(!x)
    {
        x=++cnt;
    }
    t[x].sum++;
    if(l==r)
    {
        return ;
    }
    int mid=(l+r)>>1;
    if(pos<=mid)
    {
        insert(t[x].ls,l,mid);
    }
    else
    {
        insert(t[x].rs,mid+1,r);
    }
}
void merge(int &l,int r)//直接指针合并，比原来的要好写
{
    if(!l||!r)
    {
        l=l+r;
        return ;
    }
    t[l].sum+=t[r].sum;
    ans1+=(ll )t[t[l].rs].sum*t[t[r].ls].sum;
    ans2+=(ll )t[t[l].ls].sum*t[t[r].rs].sum;
    merge(t[l].ls,t[r].ls);
    merge(t[l].rs,t[r].rs);    
}
int work(int &x)
{
    int T,ls,rs;
    x=0;
    cin>>T;
    if(!T)
    {
        work(ls);
        work(rs);
        ans1=ans2=0;
        x=ls;//指针，得用中间变量存储
        merge(x,rs);
        ans+=min(ans1,ans2);
    }
    else
    {
        pos=T;
        insert(x,1,n);
    }
}
int main()
{
    scanf("%d",&n);
    int t=0;
    work(t);
    printf("%lld",ans);
    return 0;
}

（完）