P4873 [USACO14DEC] Cow Jog_Gold 牛慢跑（乱搞？二分？）

（话说最近写的这类题不少啊。。。）

 

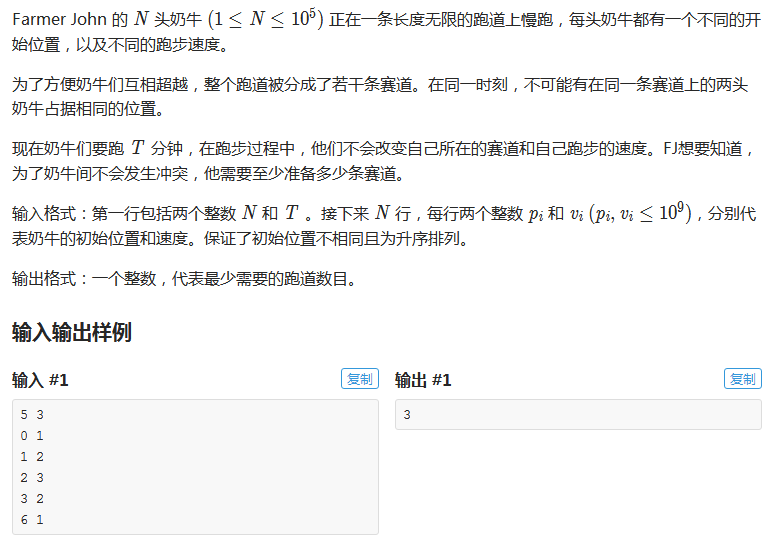
化简：给定数轴上一系列点，向正方向移动，点不能撞在一起，如果碰到一起就需要放到另外一行，求要多少行才能满足所有点不相撞的条件。

（被标签误解，老是想到二分答案。。。）

这题其实不难。首先，答案一定是最大相撞的那个点。（开的道可以共用）

然后，这题就比较明朗了。要找的就是一个点，它后面的点在t时刻堆在它头上最多。

也就是到终点的距离超过了它。

这个关系有点眼熟.....有点像逆序对啊。。。或者说，对一个点求逆序对...亦或者...最长不（上升下降不管了）子序列（对结束点求）？

那....有请我们的lower_bound上场。（每个点*-1，才能求小于等于它的最大值）

但是，发现不对....wa了不少点。

回头想想，大思路应该没有问题，一定是哪个细节的问题。

翻了翻边界，发现是最长不上升子序列，所以lower_bound的一个等号是罪魁祸首...

于是改成upper_bound就行了啊。。。

 于是不断（贪心地）更新，就能找到答案了。

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=1e6+10;
struct node
{
    ll x,v,st,ed;
}a[maxn];

ll q[maxn];
ll n,t;
ll tot;
int main()
{
    scanf("%lld%lld",&n,&t);
    for(int i=1;i<=n;i++)
    {
        ll x,y;
        scanf("%lld%lld",&x,&y);
        a[i].st=x;
        a[i].ed=x+y*t;
    }
    q[++tot]=-a[1].ed;
    for(int i=2;i<=n;i++)
    {
        ll x=-a[i].ed;
        if(x>=q[tot])
        {
            q[++tot]=x;
        }
        else
        {
            int k=upper_bound(q+1,q+tot+1,x)-q;
            q[k]=x;
        }
    }
    printf("%lld",tot);    
    return 0;
}

（完）