树链剖分复习笔记
鸽了好久的一篇博客啊....
题目描述
如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
输入输出格式
输入格式:
第一行包含4个正整数N、M、R、P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含N个非负整数,分别依次表示各个节点上初始的数值。
接下来N-1行每行包含两个整数x、y,表示点x和点y之间连有一条边(保证无环且连通)
接下来M行每行包含若干个正整数,每行表示一个操作,格式如下:
操作1: 1 x y z
操作2: 2 x y
操作3: 3 x z
操作4: 4 x
输出格式:
输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模)
输入输出样例
说明
时空限制:1s,128M
数据规模:
对于30%的数据: N≤10,M≤10
对于70%的数据: N≤103,M≤103
对于100%的数据: N≤105,M≤105
( 其实,纯随机生成的树LCA+暴力是能过的,可是,你觉得可能是纯随机的么233 )
样例说明:
树的结构如下:
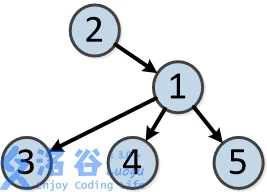
各个操作如下:

(之前一直觉得树剖非常难来着...)
树链剖分,就是把一颗树分成链们,然后用数据结构维护值.
总的来说难点就是两个dfs。
一、原理
把一棵树分成链和轻链,然后用数据结构维护。
二、几组概念
重边:父节点和他重儿子的连边
重儿子:对于非叶节点,他的儿子中以那个儿子为根的子树节点数最大的儿子为重儿子
轻边:除重边,其余全是轻边
轻儿子:每个非叶节点的儿子中,除去重儿子,其余全是轻儿子
重链:当一条链全为重边组成,其为重链。
注意:
- 对于叶节点,若其为轻儿子,则有一条以自己为起点的长度为一的链。
- 每一条重链均以轻儿子为起点,即为下面提到的TOP。
- 叶节点既没有重儿子,也没有轻儿子,因为他没有儿子。。。
- 每条边的值其实就是进行DFS时的序号。
如图

为什么呢?重链的话,我们当然希望越简单维护的东西越挨在一起,于是越长链我们把他们鸽在一起(咕咕咕)
然后把它们用线段树啊treap啊之类的维护一下就好了。
三、实现手段
(1)变量申明
struct edge { int to,next; }e[maxn]; int head[maxn],cnt; inline int addedge(int from,int to)//初步存图(树) { e[++cnt].next=head[from]; e[cnt].to=to; head[from]=cnt; } int rt=0; int son[maxn];//节点的重儿子 int size[maxn];//子树大小 int top[maxn];//重链的顶端 int dep[maxn];//深度 int dfsn[maxn];//dfs序 int fa[maxn];//点的父亲 int w[maxn];//新的点在线段树里的下标 int tot;//节点数量 struct tree//线段树 { int l,r,sum,add; }t[maxn];
要实现标记轻儿子,重儿子,我们需要子树大小,这需要dfs,深度,这也要dfs,dfs序....反正就是dfs就是了
所以
(2)dfs
void dfs1(int u)//处理的量:子树大小,深度,fa,son { size[u]=1;//首先子树大小为1(自身) dep[u]=dep[fa[u]]+1;//同lca预处理 for(int i=head[u];i;i=e[i].next) { int v=e[i].to; if(v!=fa[u])//向下遍历 { fa[v]=u; dfs1(v);//先向下 size[u]+=size[v];//再统计子树大小 if(size[son[u]]<size[v])//更新重儿子 son[u]=v;//保存重儿子 } } }
dfs1还是较好理解&&实现的跑完这样:
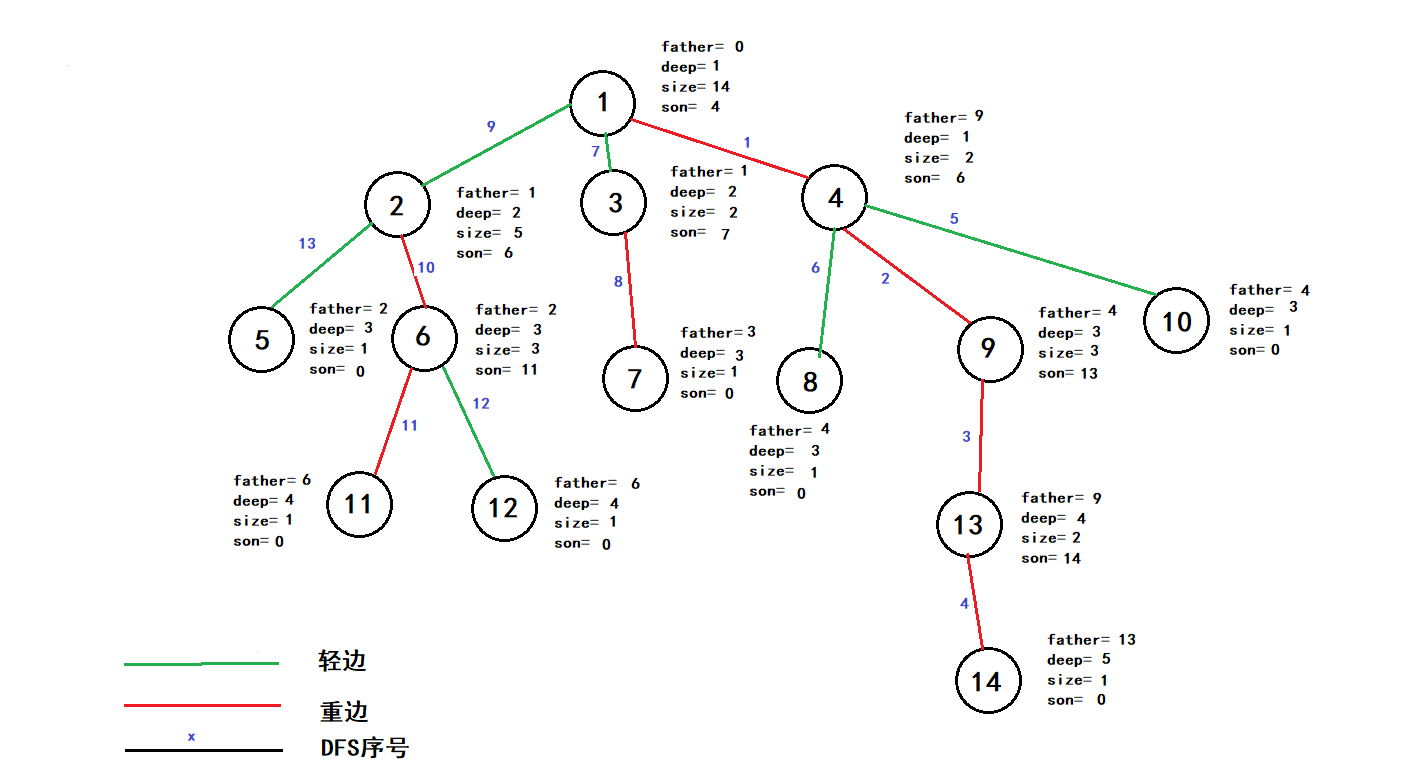
void dfs2(int u,int d)//当前点,和链顶//处理量:链顶,dfs序,新编号 { top[u]=d; dfsn[u]=++tot;//记录dfs序 w[tot]=u;//线段树里的东西 if(son[u])//如果有重儿子 dfs2(son[u],d);//继续走重儿子伸长重链 for(int i=head[u];i;i=e[i].next) { int v=e[i].to; if(v!=son[u]&&v!=fa[u])//如果v是轻儿子 dfs2(v,v);//那跟新链顶,继续向下 } }
其实到这树剖就已经差不多了跑完这样:
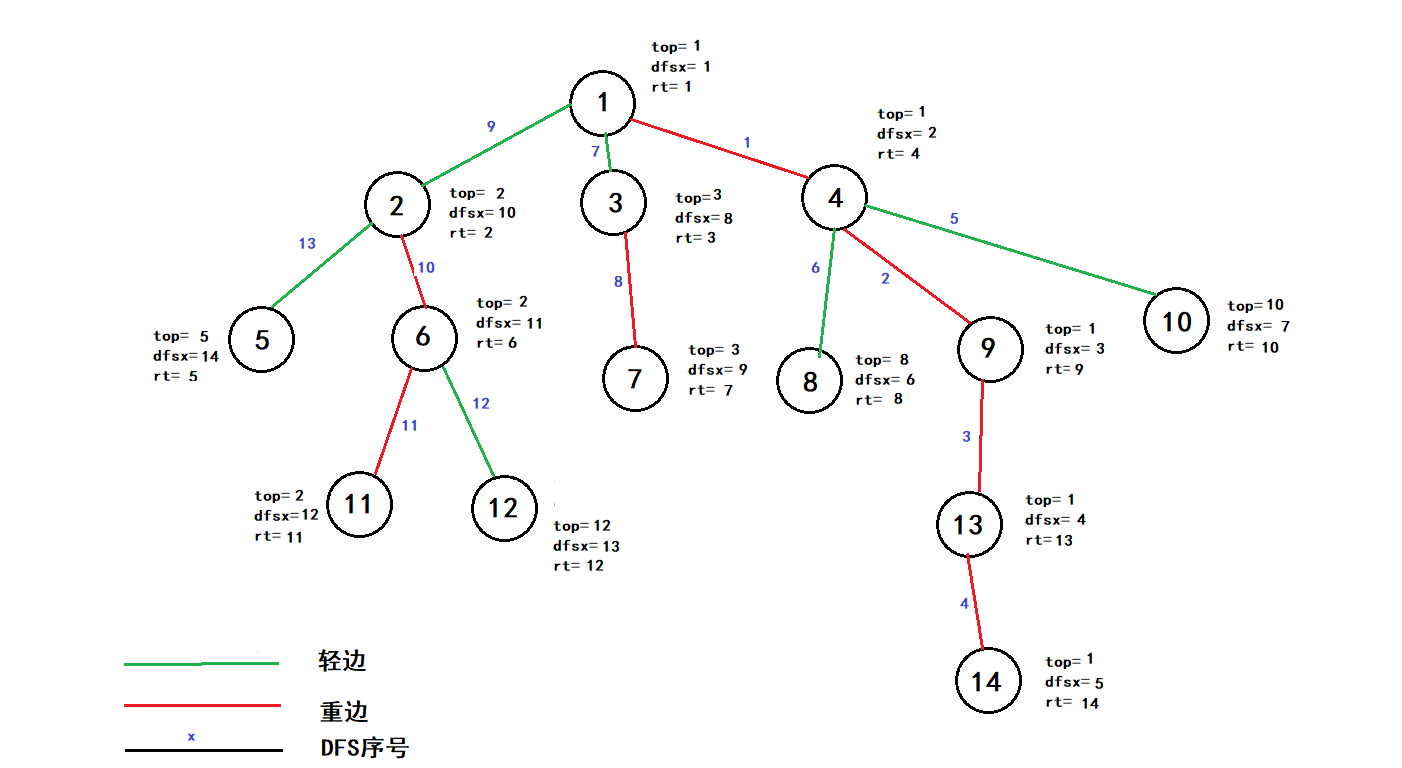
(3)数据结构
以线段树为例:

struct tree { int l, r, sum, add; } t[maxn]; void pushup(int p) { t[p].sum = (t[lc(p)].sum + t[rc(p)].sum) % mod; } int len(int p) { return t[p].r - t[p].l + 1; } void build(int l, int r, int p) { t[p].l = l; t[p].r = r; if (l == r) { t[p].sum = w[l]; return; } int mid = l + r >> 1; build(l, mid, lc(p)); build(mid + 1, r, rc(p)); pushup(p); } void spread(int p) { if (t[p].add != 0) { t[lc(p)].add = (t[lc(p)].add + t[p].add) % mod; t[rc(p)].add = (t[rc(p)].add + t[p].add) % mod; t[lc(p)].sum = (t[lc(p)].sum + t[p].add * len(lc(p))) % mod; t[rc(p)].sum = (t[rc(p)].sum + t[p].add * len(rc(p))) % mod; t[p].add = 0; } } void change(int l, int r, int k, int p) { if (l <= t[p].l && t[p].r <= r) { t[p].add = (t[p].add + k) % mod; t[p].sum = (t[p].sum + len(p) * k) % mod; return; } spread(p); int mid = t[p].l + t[p].r >> 1; if (l <= mid) change(l, r, k, lc(p)); if (r > mid) change(l, r, k, rc(p)); pushup(p); } int ask(int l, int r, int p) { if (l <= t[p].l && t[p].r <= r) { return t[p].sum % mod; } spread(p); int mid = t[p].l + t[p].r >> 1; int res = 0; if (l <= mid) res = (res + ask(l, r, lc(p))) % mod; if (r > mid) res = (res + ask(l, r, rc(p))) % mod; return res % mod; }
这样就处理好了第三第四操作~
下面,又是一个难点:
操作1和操作2.这里的处理方式有点像lca....
inline int sum(int x,int y) { int ret=0; while(top[x]!=top[y])//一直走到顶 { if(dep[top[x]]<dep[top[y]]) swap(x,y); ret=(ret+ask(dfsn[top[x]],dfsn[x],rt)%mod);//可以区间查的区间查 x=fa[top[x]];//跳上去 }
//循环之后,这两个点在同一重链上,但由于不知道是否是同一点,所以来统计一下两点的贡献 if(dfsn[x]>dfsn[y]) swap(x,y); return (ret+ask(dfsn[x],dfsn[y],rt))%mod; } inline void updates(int x,int y,int c) { while(top[x]!=top[y])//同上,能区间加的区间加 { if(dep[top[x]]<dep[top[y]]) swap(x,y); change(dfsn[top[x]],dfsn[x],c,rt); x=fa[top[x]];//跳上去 } if(dfsn[x]>dfsn[y]) swap(x,y); change(dfsn[x],dfsn[y],c,rt); }
于是,树剖基本就结束了(真的结束了)
完整代码(模板题):
#include <bits/stdc++.h> #define lc(x) x << 1 #define rc(x) x << 1 | 1 using namespace std; const int maxn = 1e6 + 10; int n, m, rt, mod; int a[maxn]; struct edge { int to, next; } e[maxn]; int head[maxn], cnt; inline void addedge(int from, int to) { e[++cnt].next = head[from]; e[cnt].to = to; head[from] = cnt; } int fa[maxn]; // int dep[maxn]; // int son[maxn]; // int size[maxn]; // int top[maxn]; // int w[maxn]; // int dfsn[maxn]; // void dfs1(int u, int f) { fa[u] = f; dep[u] = dep[f] + 1; size[u] = 1; for (int i = head[u]; i; i = e[i].next) { int v = e[i].to; if (v == f) continue; dfs1(v, u); size[u] += size[v]; if (size[son[u]] < size[v] || son[u] == 0) son[u] = v; } } int tot; void dfs2(int u, int d) { dfsn[u] = ++tot; w[tot] = a[u]; top[u] = d; if (son[u] != 0) dfs2(son[u], d); for (int i = head[u]; i; i = e[i].next) { int v = e[i].to; if (v == fa[u] || v == son[u]) continue; dfs2(v, v); } } /*~~~~~~~~~~~~~~~~~~~~~~~~~~*/ struct tree { int l, r, sum, add; } t[maxn]; void pushup(int p) { t[p].sum = (t[lc(p)].sum + t[rc(p)].sum) % mod; } int len(int p) { return t[p].r - t[p].l + 1; } void build(int l, int r, int p) { t[p].l = l; t[p].r = r; if (l == r) { t[p].sum = w[l]; return; } int mid = l + r >> 1; build(l, mid, lc(p)); build(mid + 1, r, rc(p)); pushup(p); } void spread(int p) { if (t[p].add != 0) { t[lc(p)].add = (t[lc(p)].add + t[p].add) % mod; t[rc(p)].add = (t[rc(p)].add + t[p].add) % mod; t[lc(p)].sum = (t[lc(p)].sum + t[p].add * len(lc(p))) % mod; t[rc(p)].sum = (t[rc(p)].sum + t[p].add * len(rc(p))) % mod; t[p].add = 0; } } void change(int l, int r, int k, int p) { if (l <= t[p].l && t[p].r <= r) { t[p].add = (t[p].add + k) % mod; t[p].sum = (t[p].sum + len(p) * k) % mod; return; } spread(p); int mid = t[p].l + t[p].r >> 1; if (l <= mid) change(l, r, k, lc(p)); if (r > mid) change(l, r, k, rc(p)); pushup(p); } int ask(int l, int r, int p) { if (l <= t[p].l && t[p].r <= r) { return t[p].sum % mod; } spread(p); int mid = t[p].l + t[p].r >> 1; int res = 0; if (l <= mid) res = (res + ask(l, r, lc(p))) % mod; if (r > mid) res = (res + ask(l, r, rc(p))) % mod; return res % mod; } /*~~~~~~~~~~~~~~~~~~~~~~~~~*/ void update(int x, int y, int k) { k = k % mod; while (top[x] != top[y]) { if (dep[top[x]] < dep[top[y]]) swap(x, y); change(dfsn[top[x]], dfsn[x], k, 1); x = fa[top[x]]; } if (dep[x] > dep[y]) swap(x, y); change(dfsn[x], dfsn[y], k, 1); } int query(int x, int y) { int res = 0; while (top[x] != top[y]) { if (dep[top[x]] < dep[top[y]]) swap(x, y); res = (res + ask(dfsn[top[x]], dfsn[x], 1)) % mod; x = fa[top[x]]; } if (dep[x] > dep[y]) swap(x, y); res = (res + ask(dfsn[x], dfsn[y], 1)) % mod; return res % mod; } int main() { scanf("%d%d%d%d", &n, &m, &rt, &mod); for (int i = 1; i <= n; i++) scanf("%d", &a[i]); for (int i = 1; i < n; i++) { int x, y; scanf("%d%d", &x, &y); addedge(x, y); addedge(y, x); } dfs1(rt, 0); dfs2(rt, rt); build(1, n, 1); for (int i = 1; i <= m; i++) { int f, x, y, z; scanf("%d", &f); if (f == 1) { scanf("%d%d%d", &x, &y, &z); update(x, y, z); } if (f == 2) { scanf("%d%d", &x, &y); printf("%d\n", query(x, y)); } if (f == 3) { scanf("%d%d", &x, &z); change(dfsn[x], dfsn[x] + size[x] - 1, z, 1); } if (f == 4) { scanf("%d", &x); printf("%d\n", ask(dfsn[x], dfsn[x] + size[x] - 1, 1)); } } return 0; }
(完)
图片来源:https://www.cnblogs.com/2529102757ab/p/10732188.html




