tarjan学习(复习)笔记(持续更新)(各类找环模板)
题目背景
缩点+DP
题目描述
给定一个n个点m条边有向图,每个点有一个权值,求一条路径,使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点,但是,重复经过的点,权值只计算一次。
输入输出格式
输入格式:
第一行,n,m
第二行,n个整数,依次代表点权
第三至m+2行,每行两个整数u,v,表示u->v有一条有向边
输出格式:
共一行,最大的点权之和。
输入输出样例
说明
n<=10^4,m<=10^5,0<=点权<=1000
算法:Tarjan缩点+DAGdp、
基本可以算是套路了吧,先缩点,然后tpsort,跑dp,是不是可以解决不少图论题目呢
思路:
两个数组,dfn,low。
dfn:dfs序(时间戳)
low:以u为根的子树里dfn最小的那个点(它的最早祖先)
附属数组:
st:模拟栈
co:重建图的联通快(点)
维护这两个数组,当dfn[u]=low[u]时判定为强连通分量(环)
为什么呢?
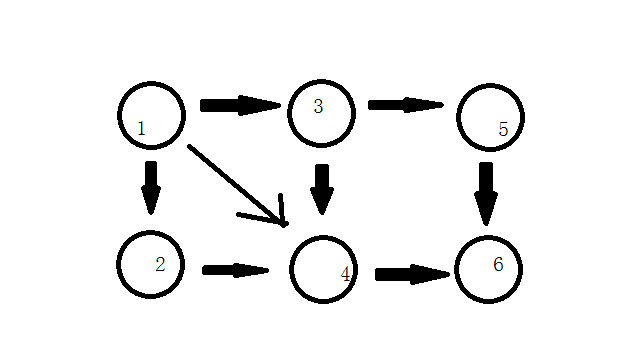
当一个点它的最老祖先等于它自己的时候,这就是一个环啊
了解四种边:
树枝边:遍历路径
前向边:爹——>儿
后向边:儿——>爹
横插边:从这个子树插到另外一个搜索子树的边
下面介绍怎么维护low
如果(u,v)是树枝边,一切好说,直接比较low[u]和low[v]的最小值即可,因为v是u的儿子,直接比较它们最早祖先的大小。
如果(u,v)是后向边或者横插边,就需要比较lou[u]和dfn[v]的最小值。
为什么?
后向边相对好理解,从这个点可以回溯到它的祖先,我们需要比较它儿子们的时间戳最小值和它祖先的时间戳 的最小值。
若之前搜到过u的祖先,那么它祖先的dfn一定是小的,但是我能从它的耳孙之间找到它的身影(自交?回交?)!
这说明什么?强连通分量!
但是,不要着急,我们需要找到强连通分量的根。所以我们需要比较一个极小值。
解释通了,那么横插边也是同理。
当dfn=low时:
也就是说它的子孙的最高祖先就是子孙本身时。
dfn时间戳正好是它子树节点的low的最小值。因为dfn值具有不重复性,所以可以断定,以它为根的子树的所有点都是一个强连通分量。
所以,可以很好地判断图的环。
注意:因为图可能不连通,所以要多次跑tarjan。
时间复杂度:由于每个点只遍历了一次,每条边也只遍历了一次,所以O(N+M)(不是spfa那么不靠谱,人家就是N+M)
给出缩点板子的代码:
#include<bits/stdc++.h> using namespace std; const int maxn=100005; struct node { int next,to; }e[maxn]; int head[maxn],cnt,sum[maxn],a[maxn]; int n,m,ru[maxn]; inline void addedge(int from,int to) { e[++cnt].next=head[from]; e[cnt].to=to; head[from]=cnt; } int dep,top; int dfn[maxn],low[maxn],vis[maxn],co[maxn],st[maxn]; void tarjan(int u) { dfn[u]=low[u]=++dep; vis[u]=1; st[++top]=u; for(int i=head[u];i;i=e[i].next) { int v=e[i].to; if(!dfn[v]) { tarjan(v); low[u]=min(low[v],low[u]); } else if(vis[v]) { low[u]=min(low[u],dfn[v]); } } if(dfn[u]==low[u])//退栈,把强连通分量薅出来 { int t; do { t=st[top--]; sum[u]+=a[t]; co[t]=u; vis[t]=0; }while(t!=u); } } int dp[maxn]; queue < int > q; void tpsort() { for(int i=1;i<=n;i++) { if(ru[i]==0&&co[i]==i) q.push(i); dp[co[i]]=sum[co[i]]; } while(!q.empty()) { int u=q.front(); q.pop(); for(int i=head[u];i;i=e[i].next) { int v=e[i].to; dp[v]=max(dp[u]+sum[co[v]],dp[v]); if(!(--ru[v])) { q.push(v); } } } } pair < int , int > g[maxn]; int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); } for(int i=1;i<=m;i++) { int x,y; scanf("%d%d",&x,&y); addedge(x,y); g[i].first=x; g[i].second=y; } for(int i=1;i<=n;i++) { if(!dfn[i]) tarjan(i); } memset(e,0,sizeof(e)); memset(head,0,sizeof(head)); cnt=0; for(int i=1;i<=m;i++) { int x=g[i].first; int y=g[i].second; if(co[x]!=co[y]) { addedge(co[x],co[y]); ru[co[y]]++; } } tpsort(); int ans=-1; for(int i=1;i<=n;i++) { ans=max(ans,dp[i]); } printf("%d",ans); return 0; }
无向图:
void tarjan(int u) { dfn[u]=low[u]=++tot; st[++top]=u; for(int i=head[u];i;i=e[i].next) { int v=e[i].to; if(!vis[i]) { vis[i]=vis[i^1]=1; if(dfn[v]==0) { tarjan(v); low[u]=min(low[u],low[v]); } else { low[u]=min(low[u],dfn[v]); } } } if(dfn[u]==low[u]) { color[u]=++col; while(st[top]!=u) color[st[top]]=col,top--; top--; } }
(完)



