矩阵乘法（乘，递推，快速幂）学习笔记

 

矩阵，是一个好东西。

大家都知道，斐波那契数列是满足如下性质的一个数列：

• f(1) = 1

• f(2) = 1

• f(n) = f(n-1) + f(n-2) (n ≥ 2 且 n 为整数)

题目描述

请你求出 f(n) mod 1000000007 的值。

输入输出格式

输入格式：

 

·第 1 行：一个整数 n

 

输出格式：

 

第 1 行： f(n) mod 1000000007 的值

 

输入输出样例

输入样例#1：

5

输出样例#1：

5

输入样例#2：

10

输出样例#2：

55

说明

对于 60% 的数据： n ≤ 92

对于 100% 的数据： n在long long(INT64)范围内。

斐波那契，基础递推吧。。但是数据范围让线性递推望而却步...

这时候，我们列出一个式子：

f(n)=f(n-1)+f(n-2);

f(n)=1*f(n-1)+1*f(n-2);

我们把f(n)和f(n-1):

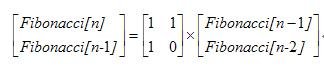
这时发现：

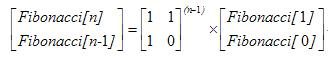
于是我们只需要计算

1 1

1 0

的n-1次方就行了。

个人对于矩阵的计算方式一直很迷...看了不少博客，都没有明白，最后自己总结了一条规律：

---

 

第一个矩阵的x行*第二个矩阵的y列，结果相加，作为结果矩阵的(x行，y列)处的数。

---

矩阵的快速幂：

即使是可以省去大量空间，一次一次推还是会超时...
n-1次方嘛，很容易想到卡速米这个东西。

其实和卡速米一样，逢二平方即可。

 于是上代码（感觉各个博客，题解的马蜂都好毒瘤啊。。）：

#include<bits/stdc++.h>
using namespace std;
const int mod=1000000007;
long long int n;
struct node
{
    long long int a[3][3];
};
node mul(node x,node y)
{
    node e;
    e.a[1][1]=e.a[1][2]=e.a[2][1]=e.a[2][2]=0;//初始化矩阵全都是0；for(int i=1;i<=2;i++)
    {
        for(int j=1;j<=2;j++)
        {
            for(int k=1;k<=2;k++)
            {
                e.a[i][j]=(e.a[i][j]+x.a[i][k]*y.a[k][j])%mod;//呱
            }
        }
    }
    return e;
}
node ksm(node x,long long int y)
{
    node ans;
    ans.a[1][1]=1;
    ans.a[1][2]=1;
    ans.a[2][1]=0;
    ans.a[2][2]=0;
    while(y)
    {
        if(y&1)
        ans=mul(ans,x); //这里是要写成赋值，我居然在这里卡了好久
        x=mul(x,x);
        y>>=1;//据说位运算能加速然而就快了1ms。。。
    }
    return ans;
}
int main()
{
    scanf("%lld",&n);//不开longlong见祖宗
    node e;
    e.a[1][1]=e.a[1][2]=e.a[2][1]=1;
    e.a[2][2]=0;//初始化1110矩阵
    if(n==1||n==2)//对n=1,2特判
    {
        printf("1");
        return 0;
    }
    node ans=ksm(e,n-2);//卡速米真好吃
    printf("%lld",ans.a[1][1]);
    return 0;
}

 

（完）