请使用π乘以你估计的任务时间(转)
add by zhj: 用PI并没什么科学依据,作者在文章结尾也提到了这点。不过,系数肯定大于1,我一般使用2
请使用π乘以你估计的时间
项目估计是一个黑色魔法,尤其是在游戏开发中更是这样。我曾经听过数理逻辑学家的一个神秘的说法,即把他们估计的时间乘以π。据实践表明,这给了他们足够的缓冲时间来处理新的需求、测试、迭代和范围内的其他变化。
因为好奇和武断,这给我留下了很深的印象,但我确实被吸引了。现在我很高兴的宣布,我已经能够为他们的循环估计猜测找到一个坚实的数学基础。

请听我解释。
某个人——一个设计者、你的领导、执行生产者、一个朋友、你的妈妈——让你做某件事。你考虑一下,草草记下一些笔记,考虑需要什么,提出一个计划和一个估计的时间。

但情况有变。发现你的设计者/生产者/领导/朋友/妈妈忽略了一些事情,而且在你工作的过程中有了一些进一步改善的想法。你的视野变大了。

当然进展不太顺利。你的第一次尝试是有益的失败。然后你急着开始第二次尝试,遇到了很多问题需要一段时间来解决。你花了额外的两天时间来考虑替换的方法。总之,你走在一条绝对曲折的路上来实现目标。
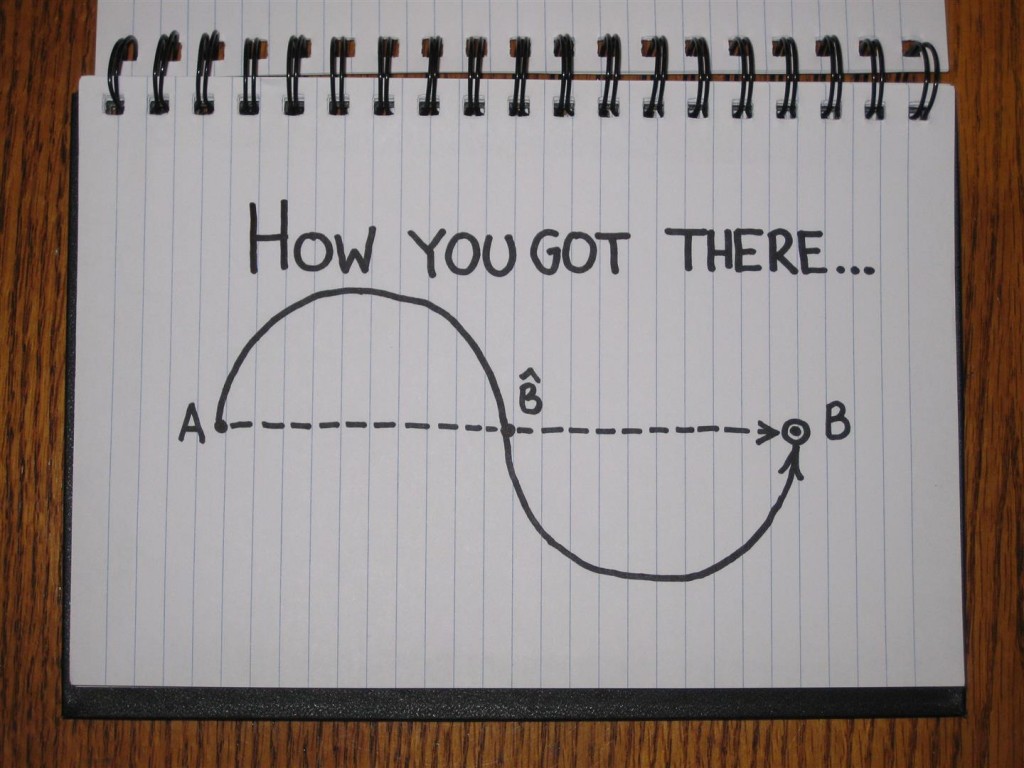
那么相比与你以前的计划,你的旅程花费了多久呢?结果是数理逻辑学家是对的。。。
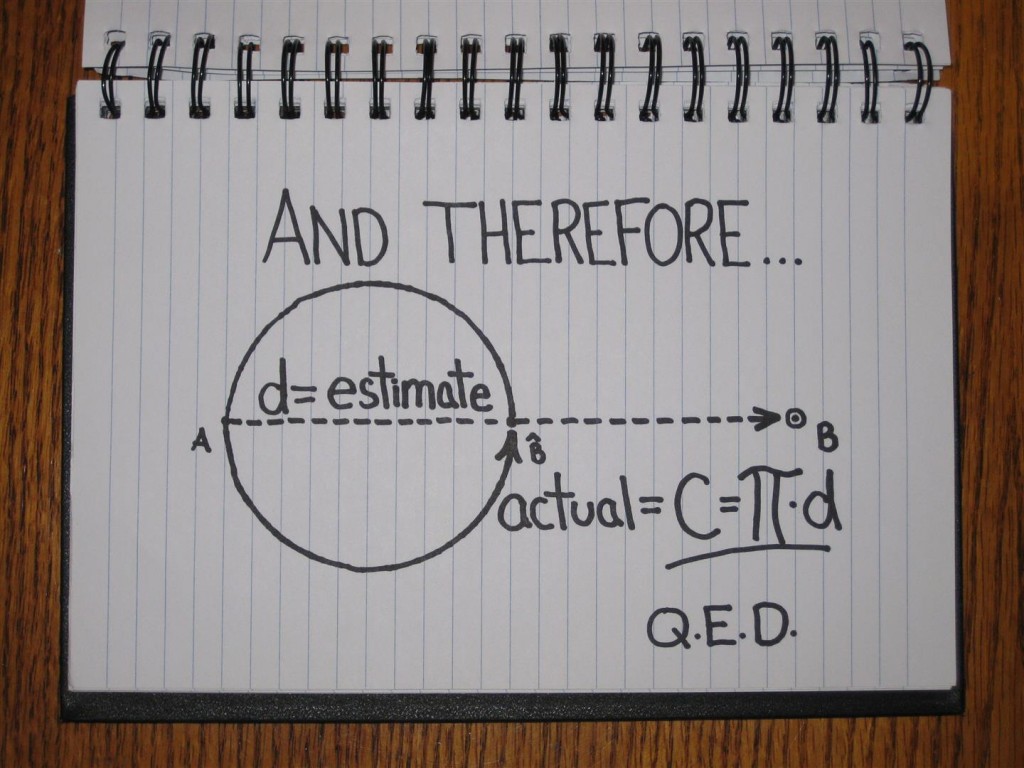
情况就是这样——无论你认为你什么时候开始,一旦你经历了研究、设计、讨论、原型、失败、测试、需求生成和创造过程中的其他一些行为时,你将无疑会在你之前计划的π倍时间完成。
现在也许有人会质疑我的数学精确性,甚至会质疑我所认为的确定的结论。人们也许会说正确的乘数不是真正的π——而应该是2,或者√2,或者e,或者黄金比例φ。然而,我确信没人会说乘数会小于一。
关于你的数理逻辑学习,重要的是你必须让自己承认——当你开始一项工程时——你无法看到全貌,你不知道情况会怎样,而且你几乎无法提前了解工作的内容。没有大量的计划和任务分析,是无法改变这个情况的,所以不要太较真。相反,给自己一个合适的缓冲,努力去工作。
噢,你上周写的那个to-do列表?你仅仅完成了列表的三分之一并不是巧合。;-)






