Core 第三组 结对作业——四则运算 Part1. Core代码编写
结对作业——四则运算 Part1. Core代码编写
PB15061303 刘梓轩
PB16061489 艾寅中
GITHUB 地址
目录 (因为内容较多,分为了三个部分,但作业系统中只能提交一次)
Part 1. Core代码编写部分
Part 2. 封装与对接相关问题
Part 3. 对于结对编程的总结与思考
项目简介
写一个能自动生成小学四则运算题目并给出答案的命令行 “软件”, 如果我们要把这个功能放到不同的环境中去(例如,命令行,Windows 图形界面程序,网页程序,手机App),就会碰到困难,因为目前代码的普遍问题是代码都散落在main ( )函数或者其他子函数中,我们很难把这些功能完整地剥离出来,作为一个独立的模块满足不同的需求。
建议大家把四则运算的计算功能包装在一个模块中(这个模块可以是一个类 Class, 一个DLL,等等), 为了方便起见,我们叫它 “计算核心”Core 模块, 这个模块至少在两个地方可以使用:
1.测试程序,这个可以是一个命令行的程序,或者是JUnit 的框架,或者是Visual Studio 单元测试的框架。这样,我们在算法层级保证了这个模块的正确性。
2.实际的软件,这是交付给最终用户的软件,有一定的界面和必要的辅助功能。
项目要求及需求分析
要求中,助教提出了一个基本的框架,就是将软件整体分为三个部分,分别为 Calc() 、Setting() 和Generate() 。现对每个部分进行需求分析。
1.Calc()
这个Calc 函数接受字符串的输入(字符串里就是算术表达式,例如 “5*3.5”,“7/8 - 3/8 ”,“3 + 90 * 0.3”等等),这个模块的返回值是一个字符串,例如,前面几个例子的结果就是(“17.5”,“1/2”,“30”)。
如果输入是有错误的,例如 “1 ++ 2”, 在数值范围是 -1000 .. 1000 的时候,传进去“10000 + 32768”,或者是“248 / 0” 怎么办?怎么告诉函数的调用者“你错了”?把返回的字符串定义为“-1” 来表示? 那么如果真的计算结果是“-1”又怎么处理呢?
建议这个时候,我们要定义各种异常(Exception),让Core在碰到各种异常情况的时候,能告诉调用者——你错了!定义要增加的功能 - 例如:支持 “运算式子格式错误” 异常
如上所述,Calc 承担了一个计算的功能,对于传进的字符串形式的表达式计算,并传出计算结果。对于如何进行表达式的计算,小组两人第一时间想到了数据结构中的利用栈进行计算的方式,但是,由于考虑到生成中缀表达式其实会带来相当程度的不便,所以最后笔者决定采取了另一种方式的表达式传入传出。避免了上述要求中第二点所提出的表达式不规范问题,详细在 Generate() 部分的需求分析及后面的代码详解中叙述。
2.Setting()
相较之下,Setting() 函数就较为简单,实际上为了简化函数中的参数传递,并且考虑到实际上最终提供的是一个封装好的代码,笔者们选择了采用全局变量作为控制相关选项的参数,而用多个bool 函数对 Setting() 进行设置,最终整合进一个 Setting() 中。
3.Generate()
Generate() 可以说是整个函数的核心部分了。因要求中实际上对于整个表达式的要求略微复杂,即显示时的括号要求,所以如果直接生成中缀表达式,优先级判断来添加括号较为复杂,所以笔者们决定直接生成后缀表达式,大大简化了 Calc() 函数。同时,个人添加了 Output() 这样一个模块,用来传出经过调整的表达式 String 。
代码详解
首先对于表达式的生成与计算,笔者们定义了如下的结构体:
typedef struct node { //the node of string char c = 0; int num = 0; int flag = -1; int frac[4] = { 0,0,0,0 }; double xiao = 0; }Node, NNode[NUMSIZE], *N_ptr;
实际上生成的表达式,就是一个由该结构体组成的串。通过 falg 的值来决定类型,即为整数 / 小数 / 分数 / 运算符,大大简化了生成和运算。
其中,int num 用来储存整数,对应的 flag 为1
char c 用来储存运算符,对应的 flag 为2
int frac 用来储存分数,分别用三个来储存 整数部分、分子和分母
double xiao 用来储存小数
接下来便是参数部分,见代码:

int _sup = 5, _inf = 1; //生成数的最大值和最小值 int _inf_len = 5, _sup_len = 9; //生成表达式长度的最大值和最小值 int _symbol =0 ; //表达式的类型,是否分数,小数等 int _row = 50; //一次生成表达式的数目 int _mi = 4; //幂次的最大 char *_oper = "+-*/"; //支持的运算符 int flag_pow = 1; //是否启用乘方运算 int _xi_disp = 5; //小数的位数 int PowerType = 0; //乘方的显示类型 ^ or ** bool set_range(int inf, int sup) { if (0 <= inf&&inf <= sup&&sup <= INT_MAX) { _inf = inf; _sup = sup; return true; } return false; }//end set_range bool set_len(int inf, int sup) { if (inf >= 2 && sup >= inf&&sup <= MAX_LEN) { _inf_len = inf; _sup_len = sup; return true; }//end if return false; }//end set_len bool set_mode(int symbol) { if (symbol == 0 || symbol == 1 || symbol == 2) { _symbol = symbol; return true; }//end if else return false; }//end set_mode bool set_row(int row) { if (row > 0 && row <= ROWSIZE) { _row = row; return true; }//end if return false; }//end set_row bool set_operator(bool add, bool min, bool mul, bool div, bool power) { //set_operator char temp[5]; for (int i = 0; i < 5; i++) { temp[i] = 0; }//end for int count = 0; if (add == true) { temp[count++] = '+'; }//end if+ if (min == true) { temp[count++] = '-'; }//end if - if (mul == true) { temp[count++] = '*'; }//end if * if (div == true) { temp[count++] = '/'; }//end if/ if (power == true) { flag_pow = 1; }//end if ^ if (count <= 0 && count > 4) return false; else { for (int i = 0; i < count; i++) { _oper[i] = temp[i]; } _oper[count] = 0; return true; } }//end set_operator bool set_file_app(int app) { //set_file: out is true if need get result into file if (File_out == 1) { if (app == 0) { File_app = 0; }//end if else if (app == 1) { File_app = 1; }//end else if return true; }//end if else { return false; }//end else }//end set_file bool set_path(bool symbol, bool reset, string pathe, string pathk) { if (symbol == true) { File_out = 1; if (reset == true) { path_exp = pathe; path_key = pathk; }//end if if (path_exp.empty() || path_key.empty()) { return false; }//end if else return true; }//end if else { File_out = 0; return true; } }//end set_path bool set_Ngenapp(bool symbol) { if (symbol == false) { N_gen_app = 0; }//end if else { N_gen_app = 1; }//end else return true; }//end set_Ngenapp bool set_PowerType(bool symbol) { //set_PowerType if (symbol == true) { PowerType = 1; return true; }//end if else { PowerType = 0; return true; }//end else }//end set_Powertype bool set_xi_disp(int symbol) { //set_xi_disp if (symbol > 0 && symbol <= Max_disp) { _xi_disp = symbol; return true; }//end if else return false; }//end set_xi_disp
可见,实际上本组的参数是较多的。原因主要是因为对于要求不断的更新,实际代码的编写过程中,笔者们先进行了整数的加减乘生成及运算,除法、分数、乘方、小数都是在后来的一个个版本中不断的加入,又因为一开始没有给相关的参数留好接口,便只好新加一些参数和判断条件。
根据代码也可见,对于处理参数的 bool 函数,里面有较为复杂的安全性判断。虽然略微显得代码有些繁琐,但这一点大大的提高了健壮性。(此处特别赞美组中的轩轩,不亏是信息安全的dalao
接下来是生成与计算部分。(代码较长

void suffix_generator() { //generate the suffix erpression //initialization N_init_suffix(suffix); int symbol = _symbol; int temp = 0, temp1;//temp variable(use for case 3) int i = 0, j = 0, k = 0;// invariable of count char oper2[10]; for (i = 0; i < int(strlen(_oper)); i++) { oper2[i] = _oper[i]; } oper2[i] = 0, i = 0; char* oper = oper2; bool flag = 0; // flag of generating operator or num int sup = _sup;// the superior bound of the num int inf = _inf; // the inferior bound of the num int count_num = 0; //the number of num in the experssion int count_oper = 0; //the number of operator in the experssion int inf_len = _inf_len;//the inferior bound of the length of expression int sup_len = _sup_len;//the superior bound of the length of expression int len_oper = strlen(oper); //the length of the operator set int length; if (inf_len == sup_len) { length = inf_len; } else { length = random(inf_len, sup_len);//the length of the exp,randomized } string string1 = oper; //end definition if (length % 2 == 0) length++; suffix[0].flag = 3; //3 ************* 3 means begin suffix[0].num = length;//store the length //end initialization temp = string1.find('/'); if (symbol == 0 && temp>0) { symbol = 3; char oper1[10]; for (i = 0, j = 0; i < len_oper; i++) { if (oper[i] != '/') { oper1[j] = oper[i]; j++; }//end if } oper1[j] = 0; oper = oper1; len_oper = strlen(oper); } switch (symbol) { case 0: //case of only intergar suffix[1].num = random(inf, sup); suffix[1].flag = 0; suffix[2].num = random(inf, sup); suffix[2].flag = 0; count_num = 2; i = 3; //end initialization while (count_num < (1 + (length - 1) / 2)) { if (count_num <= count_oper + 1) { //the prefix is full(n numbers and n-1 operators) suffix[i].flag = 0; suffix[i++].num = random(inf, sup); count_num++; }//end if else if (count_oper == ((length - 1) / 2 - 1)) { //if there is almost done,then num should not be the last suffix[i].flag = 0; suffix[i++].num = random(inf, sup); count_num++; } else { flag = srand_generator(inf, sup, (inf + sup) / 2); //generating num & operator with equal possibility if (flag == 0) { //generating the number suffix[i].flag = 0; suffix[i++].num = random(inf, sup); count_num++; }//end if else { //generating the operator suffix[i].flag = 1; if (flag_pow == 1 && suffix[i - 1].flag == 0) { temp = random(1, 20); if (temp <= 4 && suffix[i - 1].num <= _mi) { suffix[i++].c = '^'; }//end if get ^ else if (temp <= 4 && suffix[i - 1].num > _mi) { if (random(0, 1)) { suffix[i++].c = oper[random(0, len_oper - 1)]; }//end if get other else { suffix[i - 1].num = random(2, _mi); suffix[i++].c = '^'; }//end else get '^' but need a change on suffix[i-1] }//end else if possibly get '^' else { suffix[i++].c = oper[random(0, len_oper - 1)]; }//end if no get '^' }//end if can get ^ else { suffix[i++].c = oper[random(0, len_oper - 1)]; } count_oper++; }//end else }//end else }//end while break;//end case 0 case 1: //initialization set_num_suffix(suffix[1], inf, sup, oper); set_num_suffix(suffix[2], inf, sup, oper); count_num = 2; i = 3; //end initialization while (count_num < (1 + (length - 1) / 2)) { if (count_num <= count_oper + 1) { //the prefix is full(n numbers and n-1 operators) set_num_suffix(suffix[i++], inf, sup, oper); count_num++; }//end if else if (count_oper == ((length - 1) / 2 - 1)) { //if there is almost done,then num should not be the last set_num_suffix(suffix[i++], inf, sup, oper); count_num++; } else { flag = srand_generator(inf, sup, (inf + sup) / 2); //generating num & operator with equal possibility if (flag == 0) { //generating the number set_num_suffix(suffix[i++], inf, sup, oper); count_num++; }//end if else { //generating the operator suffix[i].flag = 1; if (flag_pow == 1 && suffix[i - 1].flag == 0) { temp = random(1, 20); if (temp <= 4 && suffix[i - 1].num <= _mi) { suffix[i++].c = '^'; }//end if get ^ else if (temp <= 4 && suffix[i - 1].num > _mi) { if (random(0, 1)) { suffix[i++].c = oper[random(0, len_oper - 1)]; }//end if get other else { suffix[i - 1].num = random(2, _mi); suffix[i++].c = '^'; }//end else get '^' but need a change on suffix[i-1] }//end else if possibly get '^' else { suffix[i++].c = oper[random(0, len_oper - 1)]; }//end if no get '^' }//end if can get ^ else { suffix[i++].c = oper[random(0, len_oper - 1)]; } count_oper++; }//end else }//end else }//end while break; case 2: //生成小数**************** suffix[1].xiao = random_d(inf, sup); suffix[1].flag = 3; suffix[2].xiao = random_d(inf, sup); suffix[2].flag = 3; count_num = 2; i = 3; //end initialization while (count_num < (1 + (length - 1) / 2)) { if (count_num <= count_oper + 1) { //the prefix is full(n numbers and n-1 operators) suffix[i].flag = 3; suffix[i++].xiao = random_d(inf, sup); count_num++; }//end if else if (count_oper == ((length - 1) / 2 - 1)) { //if there is almost done,then num should not be the last suffix[i].flag = 3; suffix[i++].xiao = random_d(inf, sup); count_num++; } else { flag = srand_generator(inf, sup, (inf + sup) / 2); //generating num & operator with equal possibility if (flag == 0) { //generating the number suffix[i].flag = 3; suffix[i++].xiao = random_d(inf, sup); count_num++; }//end if else { //generating the operator suffix[i].flag = 1; if (flag_pow == 1 && suffix[i - 1].flag == 0) { temp = random(1, 20); if (temp <= 4 && suffix[i - 1].xiao <= double(_mi)) { suffix[i++].c = '^'; }//end if get ^ else if (temp <= 4 && suffix[i - 1].num > double(_mi)) { if (random(0, 1)) { suffix[i++].c = oper[random(0, len_oper - 1)]; }//end if get other else { suffix[i - 1].xiao = random_d(2, _mi); suffix[i++].c = '^'; }//end else get '^' but need a change on suffix[i-1] }//end else if possibly get '^' else { suffix[i++].c = oper[random(0, len_oper - 1)]; }//end if no get '^' }//end if can get ^ else { suffix[i++].c = oper[random(0, len_oper - 1)]; } count_oper++; }//end else }//end else }//end while break;//end case 0 break; case 3: //case of only intergar,with / suffix[1].num = random(inf, sup); suffix[1].flag = 0; suffix[2].num = random(inf, sup); suffix[2].flag = 0; count_num = 2; i = 3; //end initialization while (count_num < (1 + (length - 1) / 2)) { if (srand_generator(10, 20, 15)) { if (count_num <= ((length - 1) / 2 - 1)) { temp = random(inf, int(floor(sqrt(sup)))); temp1 = random(inf, int(floor(sqrt(sup)))); suffix[i].num = temp1*temp; suffix[i++].flag = 0; suffix[i].num = temp; suffix[i++].flag = 0; suffix[i].c = '/'; suffix[i++].flag = 1; count_num += 2; count_oper++; }//if no out of range else continue; }//end if else { if (count_num <= count_oper + 1) { //the prefix is full(n numbers and n-1 operators) suffix[i].flag = 0; suffix[i++].num = random(inf, sup); count_num++; }//end if else if (count_oper == ((length - 1) / 2 - 1)) { //if there is almost done,then num should not be the last suffix[i].flag = 0; suffix[i++].num = random(inf, sup); count_num++; } else { flag = srand_generator(inf, sup, (inf + sup) / 2); //generating num & operator with equal possibility if (flag == 0) { //generating the number suffix[i].flag = 0; suffix[i++].num = random(inf, sup); count_num++; }//end if else { //generating the operator suffix[i].flag = 1; if (flag_pow == 1 && suffix[i - 1].flag == 0) { temp = random(1, 20); if (temp <= 4 && suffix[i - 1].num <= _mi) { suffix[i++].c = '^'; }//end if get ^ else if (temp <= 4 && suffix[i - 1].num > _mi) { if (random(0, 1)) { suffix[i++].c = oper[random(0, len_oper - 1)]; }//end if get other else { suffix[i - 1].num = random(2, _mi); suffix[i++].c = '^'; }//end else get '^' but need a change on suffix[i-1] } else { suffix[i++].c = oper[random(0, len_oper - 1)]; }//end if no get '^' }//end if can get ^ else { suffix[i++].c = oper[random(0, len_oper - 1)]; }//end if no get '^' count_oper++; }//end else }//end else }//end else }//end while break;//end case 3 } while (count_oper < (length - 1) / 2) { //fill the last operator suffix[i].flag = 1; suffix[i++].c = oper[random(0, len_oper - 1)]; count_oper++; }//end while suffix[i].flag = -1;// not need }//end suffix_generator

int calculate() { //calculate the suffix //symbol decides the type of calculation //未考虑分数,小数,真分数,返回整数 //未考虑中间出现负数 Nsqstack s; Ninitstack(s); int symbol = _symbol; int length = suffix[0].num;//the length of exp int len_num = (length + 1) / 2; int len_oper = (length - 1) / 2; if (length >= 3) { Npush(s, suffix[1]); Npush(s, suffix[2]); } else return -10000; Node suffix_left, suffix_right, suffix_result; init_suffix(suffix_left); init_suffix(suffix_right); init_suffix(suffix_result); int i = 3; int left = 0, right = 0;//left number and right number use in case 0&1 double left_d = 0, right_d = 0;//left number and right number use in case 2 char op = 0; //operator int result = -1; //result use in case0&1 double result_d = -1; switch (symbol) { case 0: //all the num is integar while (i <= length) { init_suffix(suffix_result); if (suffix[i].flag == 0) { //get a num Npush(s, suffix[i]); i++; }//end if else if (suffix[i].flag == 1) { //get a operator Npop(s, suffix_right); right = suffix_right.num; Npop(s, suffix_left); left = suffix_left.num; op = suffix[i].c; result = cal(left, right, op); if (result <= -1) return -1; else if (result == -10000) return -10000; suffix_result.num = result; suffix_result.flag = 0; Npush(s, suffix_result); i++; }//end else if }//end while Npop(s, _suffix_result); result = suffix_result.num; break; //end case 0 case 1: //the num includes fracs&integars while (i <= length) { init_suffix(suffix_result); if (suffix[i].flag == 0 || suffix[i].flag == 2) { //get a num Npush(s, suffix[i]); i++; }//end if else if (suffix[i].flag == 1) { //get a operator Npop(s, suffix_right); Npop(s, suffix_left); op = suffix[i].c; result = cal(suffix_left, suffix_right, suffix_result, op); if (result == -10000) return -10000;//error else if (result == -1) return -1;//get <0 Npush(s, suffix_result); i++; }//end else if }//end while Npop(s, _suffix_result); return 1; break; //end case 1 case 2: //get result ofxiaoshu while (i <= length) { init_suffix(suffix_result); if (suffix[i].flag == 3) { //get a num Npush(s, suffix[i]); i++; }//end if else if (suffix[i].flag == 1) { //get a operator Npop(s, suffix_right); right_d = suffix_right.xiao; Npop(s, suffix_left); left_d = suffix_left.xiao; op = suffix[i].c; result = cal(left_d, right_d, op, result_d); if (result <= -1) return -1; else if (result == -10000) return -10000; suffix_result.xiao = result_d; suffix_result.flag = 3; Npush(s, suffix_result); i++; }//end else if }//end while Npop(s, _suffix_result); result = int(suffix_result.xiao); break; //end case 2 } return result; }//end calculate ,return int*********
可见,两个函数的参数都较为简单(明明就是没有参数啊喂)。原因还是因为前述的,所支持的类型不断的增加,参数也是改了又改。于是最后就决定利用一个全局变量来储存生成的式子的答案了。
实际的生成与计算函数思路较为明确,就是根据相关的参数,来决定是否调用不同的 random 函数。而计算由于直接生成了后缀表达式,所以只需要利用一个栈来计算就好了。
为了表达式的正确性,代码中仍有一些小的细节调整。即:对于一个后缀表达式来说,前两个一定是运算数,而不会是运算符;运算符的数目一定是运算数少1。因此,只要先生成两个运算数,接着再按照规定的数目生成足够的运算符和运算数,即一定可以保证表达式的正确性。
接下来的问题,就是如何把后缀表达式转换为一个中缀表达式的 string了,代码实现如下:

string needbracket(string a, char c, int which) { //suffix get char by char int len = a.length(); if (len < 3) return a; int flag = 0; switch (c) { case'+': return a; break; case'-': { if (which == 1) { for (int i = 0; i < len; i++) { if (a[i] == '+' || a[i] == '-') flag = 1; if (a[i] == ')') flag = 0; } if (flag == 1) { string c = "("; c += a; c += ")"; return c; } } else { return a; } } ; break; case'*': { for (int i = 0; i < len; i++) { if (a[i] == '+' || a[i] == '-') flag = 1; if (a[i] == ')') flag = 0; } if (flag == 1) { string c = "("; c += a; c += ")"; return c; } } ; break; case'/': { if (which == 1) { for (int i = 0; i < len; i++) { if (a[i] > 41 && a[i] < 48) flag = 1; if (a[i] == ')') flag = 0; } if (flag == 1) { string c = "("; c += a; c += ")"; return c; } } else { for (int i = 0; i < len; i++) { if (a[i] == '+' || a[i] == '-') flag = 1; if (a[i] == ')') flag = 0; } if (flag == 1) { string c = "("; c += a; c += ")"; return c; } } } ; break; case'^': { for (int i = 0; i < len; i++) { if (a[i] > 41 && a[i] < 48) flag = 1; if (a[i] == ')') flag = 0; } if (flag == 1) { string c = "("; c += a; c += ")"; return c; } } ; break; } return a; }//end needbracket void getnormalsuffix(int key, int NUM) { stack<string> Expression; string next; string last; string delete_zero; char lastop = 0; int flag = 0; for (int i = 1; i <= suffix[0].num; i++) { // if is a num/frac then change to string else change to mid if (suffix[i].flag == -1) break; else if (suffix[i].flag == 0) { Expression.push(to_string(suffix[i].num)); flag++; //cout << suffix[i].num << ' '; }//end elseif else if (suffix[i].flag == 2) { //cout << suffix[i].frac[1] << '`' << suffix[i].frac[2] << '/' << suffix[i].frac[3] << ' '; string c; if (suffix[i].frac[1] != 0) { c += to_string(suffix[i].frac[1]); c += '`'; }//end if c += to_string(suffix[i].frac[2]); c += '/'; c += to_string(suffix[i].frac[3]); Expression.push(c); flag++; }//end elseif else if (suffix[i].flag == 3) { delete_zero = to_string(suffix[i].xiao); for (int j = delete_zero.length(); delete_zero[j - 1] == '0'; j--) { delete_zero.erase(j - 1); } Expression.push(delete_zero); flag++; } else { next = Expression.top(); Expression.pop(); last = Expression.top(); Expression.pop(); if (flag == 0) { next = needbracket(next, suffix[i].c, 1); last = needbracket(last, suffix[i].c, 0); }//end if else { if (flag == 1) { last = needbracket(last, suffix[i].c, 0); }//end else }//end else last += ' '; if (suffix[i].c == '^') { if (PowerType == 1) last += suffix[i].c; else last += "**"; } else { last += suffix[i].c; } last += ' '; last += next; Expression.push(last); lastop = suffix[i].c; //cout << suffix[i].c << ' '; flag = 0; }//end else }//end for expression = Expression.top(); cout << endl << expression << " " << endl; }//end getnormalsuffix string quantize(string exp, int i) { if (exp[i] < '5') { exp.erase(i); return exp; } else { exp.erase(i); for (int len = exp.length(); i > 0; ) { if (exp[i - 1] == '.') i--; exp[--i]++; if (exp[i] > '9') { exp[i] = '0'; }//end if else return exp; }//end for if (exp[i] == '0') { string temp = "1"; exp[i] = '0'; temp += exp; return temp; } } }
同样使用了栈来辅助,其实思路和 Calc() 几乎是一样的,遍历表达式串,如果是数字,进栈,如果是运算符,从栈中取出两个元素进行运算,只不过这个地方是一个字符串的相加,然后利用的栈也是一个字符串类型的栈。
而 needbrack 函数,即是用来给表达式添加合适的括号。简单来说,其逻辑即为读到一个运算符,根据运算符的优先级,来加括号。遍历运算符两边的表达式,如果出现了低优先级的运算符没有被括号“保护”起来,才加括号,从而避免了多余的括号。
从头到尾最让我头疼的一个要求莫过于查重的要求了,但实际上静下心来看看这个要求其实没那么难,先贴上代码:

bool repeated() { int len = suffix[0].num; //suffix[0] 用来储存式子的长度 int char_location = (len + 1) / 2; //串中运算符开始的位置 for (int i = 0; char_location <= len; char_location++, i++;) { if (suffix[char_location].c == '+' || suffix[char_location].c == '*') { for (int num_of_exp = 0; num_of_exp < expressions.size(); num_of_exp++;) { if (suffix[i] == expression[num_of_exp][i]) return -1; int flag = 0; for (int j = i; j <= len; j++) { if (suffix[j] != expression[num_of_exp][j]) flag = 1; }//end for if (flag == 0) return -1; }//end for }//end if else continue; }//end for return }
实际可见代码并不长,但嵌套了三个循环。
一开始本身准备对于产生的中缀表达式来进行查重,但是,在转换中缀表达式的 string 的过程中,为了美观添加了大量的空格,加大了操作难度。后来笔者提出对于我们的表达式结构体串来进行操作。
首先,笔者们重新修改了表达式的生成函数,形成了一种更加完全的后缀表达式,例如:
普通的后缀表达式:
3 5 * 2 - 7 /
完全的后缀表达式:
7 2 3 5 * - /
两者实际表达的是同一个运算
对于重复的定义是,可以通过有限次的运算,转化为同一个式子。笔者们便有了如下思路,如果将每一个可以左右交换的运算符(+和*)两边的表达式遍历比较,如果完全相同,便可以得到结果。转换成上述的那种完全后缀的表达式,也更加方便了这样的操作。从代码可见,除了嵌套的循环多了点,其他都好。
同时,由于原始表达式中的数字都是用 int/double 来储存的,比起 string 的比较,速度有所提升。
测试结果
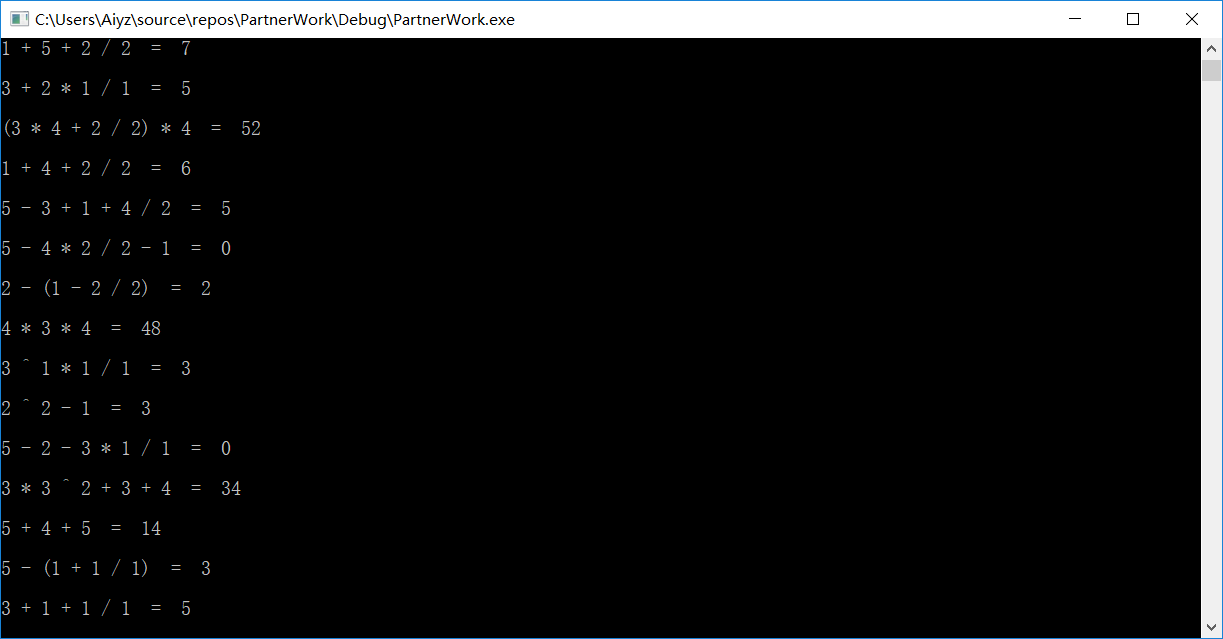

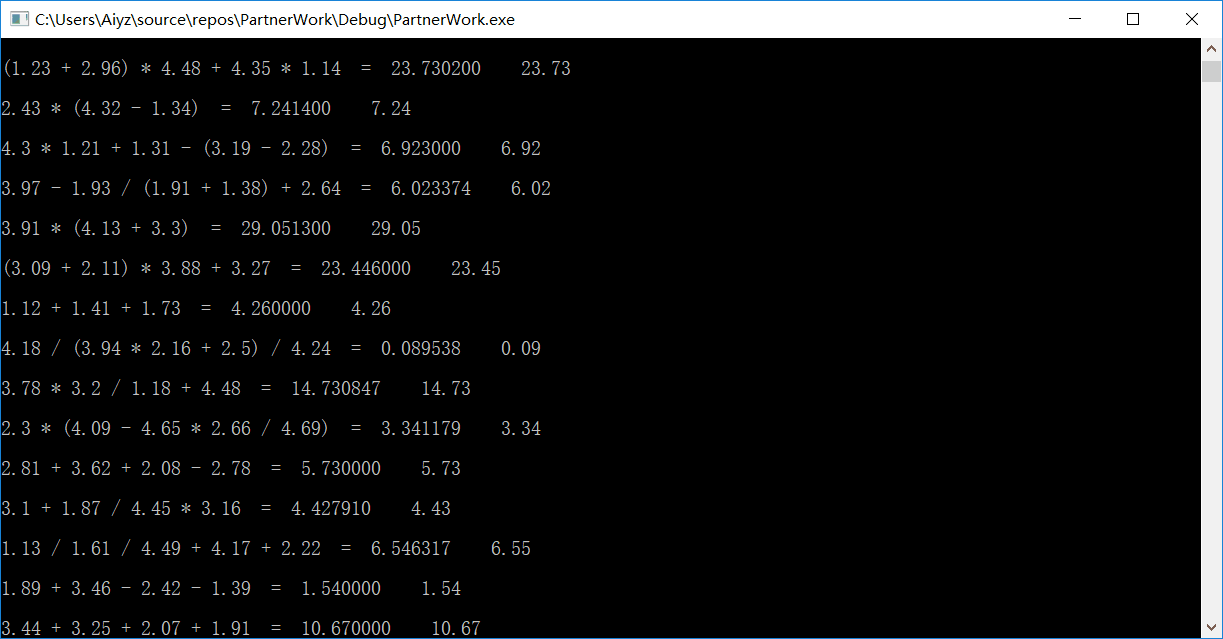
如图可见,测试结果良好。且对于小数位数的四舍五入效果较好
BUG相关
笔者们特意记录了编写过程中所出现的 BUG,现罗列如下:
在转化中缀表达式这个过程中,出现了一个较为难发现的问题。即“减号和除号后面要变号”。起初笔者们在给表达式添加括号时,仅仅判断是否新的运算符优先级更高,却忘了这一条,结果出现了这种如果不仔细看十分难以发现的问题
例如:3 2 1 - - 一式,如果仅仅由运算符的优先级遍历判断,- 号属于最低的优先级,因此出来的结果不会加括号,就出现了:3 - 2 - 1 = 1 这样的结果,一开始也没有想到这个问题。多亏了结对伙伴慧眼明察,后来负责这部分的笔者几乎重新写了整个 needbrack 函数,行数扩充了5倍
再如:在生成式子的时候,因为用户的需求,在写的过程中遇到了很多意想不到的bug。比如一开始我们并没有考虑到整数除法必须得到整除的结果的需求。而在获知该需求以后,我们经历了一些困难,代码的结构也因此发生了一定的变动,而正是这样的变动,使得我们接下来遇到了新的问题。
由于结构的改变,导致本来写好的乘方的计算又出现了问题。因为乘方的幂次和出现程度不能太高,否则的话很容易使得结果溢出,我们只得再次为了乘方对计算模块的结构作出改动。把本来读取字符串中的乘方字符改为用bool型指示变量,然而这个改变又带来了新的问题。由于乘方不在字串中,一旦用户只选择乘方来计算,那么我们的生成模块就会因为输入的是空串导致溢出。为此我们不得不再次对生成模块进行改动,最后原本很流畅的代码被改得面目全非,即使我们已经尽最大的努力使其维持原来的结构,但不得不说,这对我们的调试工作和维护代码工作都带来了很大的影响。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号