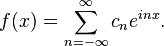稀疏学习之设计字典
稀疏信号的一个最重要的部分就是字典A。那么选择A?怎么样选择才是合理?
一、字典的选择和学习
如何选择合适的字典,一种基本的方法是选择预定义的字典,如无抽样小波、可操纵小波、轮廓博、曲波,等等。近期很多学者提出来主要针对图像的字典,特别是类似于“卡通”的图像内容,假设分段平滑并具有平滑边界。
这些提出的字典附有详细的理论分析,能够对简单信号建立稀疏表示系数。一个典型的应用时M项近似衰减率——用M个最佳的非零系数表示信号。
另一种选择字典的方法是可调节的——通过在特定参数(连续或者离散的)控制下生成基或帧。两个最熟知的例子就是小波包和Bandelets.
尽管预定义和自适应的字典通常具有较快的变换速度,他们无法处理稀疏信号,并且,这些字典限制于特定类型的图像和信号,无法应用于新的,任意类型的信号。因此我们需要寻找克服这些限制的新方法——通过一种学习的观点。
基于学习的方法首先需要构建一个训练信号集,然后构建一个经验学习字典,即通过经验数据中生成潜在的原子,而不通过理论模型。这样的字典可以实际应用,作为固定或冗余字典。
与预定义和自适应的字典不同,学习字典能够适用于符合稀疏场定义的任何类型的信号。然而,这将带来更重的计算负担,且只能应用于低维信号(至少目前为止是这样的)这是为什么这种方法只能应用于图像块。
二、字典学习算法
2.MOD算法
显然,没有一种通用的算法可以求解(12.1)和(12.2),和我们无法求解(P0)的原因类似。然而,没有理由我们不去寻找一个启发式算法,并研究它在特殊情况下的执行表现。
我们可以将(12.1)看成一种嵌套最小化策略:在第k步,我们利用第k-1步得到字典A(k-1),对数据库中的M个实例yi求解对应的 :这可以得到矩阵
,然后我们通过最小二乘法求解
:
这里我们使用了Frobenius范数来评价误差(矩阵的F范数为矩阵中所有元素的平方和的平方根)。允许对获得的字典的元素进行缩放。递增k并重复上述循环,直到满足收敛准则。这样的块坐标松弛算法首先由Engan提出,称为最优方向法(Method of Optimal Direction,MOD),这个算法描述如图12.1
以下是本人对MOD算法的理解
1,匹配追踪算法
在分析该算法前,先介绍下匹配追踪算法
匹配追踪最早是时频分析的分析工具,目的是要将一已知讯号拆解成由许多被称作为原子讯号的加权总和,而且企图找到与原来讯号最接近的解。其中原子讯号为一极大的原子库中的元素。以数学式子表示可以得到:
其中, 是权重,
是权重,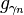 是由字典D中获得的原子讯号。
是由字典D中获得的原子讯号。
如同傅立叶级数将一讯号拆解成一系列的正弦波的相加,其中每个成分拥有不同的系数作为权重,其数学式子如下:
而匹配追踪也具有将讯号拆解成一系列原子相加的意涵,而甚至可以使用匹配追踪去描述傅立叶级数,也就是原子库对应到的所有正弦函数的集合
2.贪婪算法
为了找到最符合原讯号的一组原子加权总合,如果对原子库进行所有组合的尝试过于耗费时间。在1993年由Mallat S和Zhang Z的论文[1]中,提出了一个贪婪算法(Greedy Algorithm),并大幅降低找出近似解的时间。其作法首先在原子库中寻找与原讯号内积结果最大的原子,找到此讯号以及其内积结果 之后再将原讯号减掉
之后再将原讯号减掉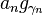 作为下一次重复运算的原始讯号,如此反复做下去即可得到一系列的
作为下一次重复运算的原始讯号,如此反复做下去即可得到一系列的 以及原子,直到达到停止条件为止,其详细的算法如下:
以及原子,直到达到停止条件为止,其详细的算法如下:
- 输入: Signal:
 , dictionary
, dictionary  .
. - 输出: List of coefficients:
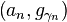 .
. - 初始化:
 ;
;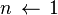 ;
;- 重复:
- find
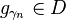 with maximum inner product
with maximum inner product 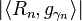 ;
; 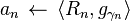 ;
; ;
;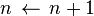 ;
;- 直到达到停止条件,例如:
 )
) - 此时的
是稀疏表示的
3.字典更新
2中的 即为此式中的
,将其代入,求解该方程的最小值,