稀疏编码学习笔记整理（一）

最近新入手稀疏编码，在这里记录我对稀疏编码的理解（根据学习进度不断更新中）

一，稀疏编码的概述

      稀疏编码的概念来自于神经生物学。生物学家提出，哺乳类动物在长期的进化中，生成了能够快速，准确，低代价地表示自然图像的视觉神经方面的能力。我们直观地可以想象，我们的眼睛每看到的一副画面都是上亿像素的，而每一副图像我们都只用很少的代价重建与存储。我们把它叫做稀疏编码，即Sparse Coding.

     1959年,David Hubel和Toresten Wiesel通过对猫的视觉条纹皮层简单细胞感受野的研究得出一个结论:主视皮层V1区神经元的感受野能对视觉感知信息产生一种“稀疏表示”.基于这一知识。

     1961年,H.B.Barlow[5]提出了“利用感知数据的冗余”进行编码的理论.

     1969年,D.J.Willshaw和O.P.Buneman等人提出了基于Hebbian 学习的局部学习规则的稀疏表示模型.这种稀疏表示可以使模型之间有更少的冲突,从而使记忆能力最大化.Willshaw模型的提出表明了稀疏表示非常有利于学习神经网络中的联想.

     1972年,Barlow推论出在稀疏性(Sparsity)和自然环境的统计特性之间必然存在某种联系.随后,有许多计算方法被提出来论证这个推论,这些方法都成功地表明了稀疏表示可以体现出在大脑中出现的自然环境的统计特性.

     1987年,Field提出主视皮层V1区简单细胞的感受野非常适于学习视网膜成像的图像结构,因为它们可以产生图像的稀疏表示.基于这个结论,1988年,Michison明确提出了神经稀疏编码的概念,然后由牛津大学的E.T.Roll 等人正式引用.随后对灵长目动物视觉皮层和猫视觉皮层的电生理的实验报告,也进一步证实了视觉皮层复杂刺激的表达是采用稀疏编码原则的.

     1989年,Field提出了稀疏分布式编码(Sparse Distributed Coding)方法.这种编码方法并不减少输入数据的维数,而是使响应于任一特殊输入信息的神经细胞数目被减少,信号的稀疏编码存在于细胞响应分布的四阶矩(即峭度Kurtosis)中.

     1996年,Olshausen和Field在Nature杂志上发表了一篇重要论文指出,自然图像经过稀疏编码后得到的基函数类似于V1区简单细胞感受野的反应特性.这种稀疏编码模型提取的基函数首次成功地模拟了V1区简单细胞感受野的三个响应特性:空间域的局部性、时域和频域的方向性和选择性.考虑到基函数的超完备性(基函数维数大于输出神经元的个数),Olshausen 和Field在1997年又提出了一种超完备基的稀疏编码算法,利用基函数和系数的概率密度模型成功地建模了V1区简单细胞感受野.

     1997年,Bell和Sejnowski 等人把多维独立分量分析(Independent Component Analysis, ICA)用于自然图像数据分析,并且得出一个重要结论:ICA实际上就是一种特殊的稀疏编码方法.

     21世纪以来,国外从事稀疏编码研究的人员又提出了许多新的稀疏编码算法,涌现出了大量的稀疏编码方面的论文,国内研究者在稀疏编码算法和应用方面也作了一些工作],但远远落后于国外研究者所取得的成果.

     稀疏编码的目的：在大量的数据集中，选取很小部分作为元素来重建新的数据。

    稀疏编码难点：其最优化目标函数的求解。

二，稀疏线性模型

    X为一个n为特征向量，可以是一个小波信号，可以是一副图片等。

D为标准化的基础矩阵，由组成元素的基本原子构成，也称为字典。在信号中可以是不同频率的波形，在图像中可以是构成图像的基本边，角。

X可以由D中和少量原子线性组合而成，及其表示系数为稀疏。如下：

 

三、数学模型

引出稀疏表示的两个基本要求 1：尽可能与原特征相似

                                       2 : 系数为稀疏。

    有上图中，我们要求p>m，根据线性代数的知识我们知道，稀疏系数有无穷多组的解。根据稀疏的条件，我们可以在所有的可行解中挑出非零元素最少的解，也就是满足稀疏性。于是得到如下的数学模型：

 

如果再考虑噪声的话，就得到如下的模型:

目标函数中为L0范数约束，是非确定性多项式（NP）难题，即是指可以在多项式时间内被非确定机(他可以猜,他总是能猜到最能满足你需要的那种选择,如果你让他解决n皇后问题,他只要猜n次就能完成----每次都是那么幸运)解决的问题.

有人做了一个证明，在一定条件下，上述的最优化问题有唯一的解。

Terry tao又证明了，在满足一定条件下，零范数问题与一范数问题是等价的。于是上述模型转化为：

 

 

四、L0范数与L1范数

      L0范数是指向量中非0的元素的个数。如果我们用L0范数来规则化一个参数矩阵W的话，就是希望W的大部分元素都是0。这太直观了是不是？，换句话说，让参数W是稀疏的。OK，看到了“稀疏”二字，大家应该意识到，原来用的漫山遍野的“稀疏”就是通过这玩意来实现的。但是看到的papers世界中，稀疏不是都通过L1范数来实现吗？这个时候你又该怀疑了，脑海里是不是到处都是||W||₁影子呀！几乎是抬头不见低头见。没错，这就是这节的题目把L0和L1放在一起的原因，因为他们有着某种不寻常的关系。那我们再来看看L1范数是什么？它为什么可以实现稀疏？为什么大家都用L1范数去实现稀疏，而不是L0范数呢？

     L1范数是指向量中各个元素绝对值之和，也有个美称叫“稀疏规则算子”（Lasso regularization）。现在我们来分析下这个价值一个亿的问题：为什么L1范数会使权值稀疏？有人可能会这样给你回答“它是L0范数的最优凸近似”。实际上，还存在一个更美的回答：任何的规则化算子，如果他在W_i=0的地方不可微，并且可以分解为一个“求和”的形式，那么这个规则化算子就可以实现稀疏。这说是这么说，W的L1范数是绝对值，|w|在w=0处是不可微，但这还是不够直观。这里因为我们需要和L2范数进行对比分析。所以关于L1范数 的直观理解，请待会看看第二节。

     那么还有一个问题：既然L0可以实现稀疏，为什么不用L0，而要用L1呢？本人查资料理解为两点：

                             1.因为L0范数很难优化求解（NP难问题）

                             2.L1范数是L0范数的最优凸近似，而且它比L0范数要容易优化求解。所以大家才把目光和万千宠爱转于L1范数。

      小结：L1范数和L0范数可以实现稀疏，L1因具有比L0更好的优化求解特性而被广泛应用。

      好，到这里，我们大概知道了L1可以实现稀疏，但我们会想呀，为什么要稀疏？让我们的参数稀疏有什么好处呢？这里扯两点：

1）特征选择(Feature Selection)：

传统的pattern recognition为：

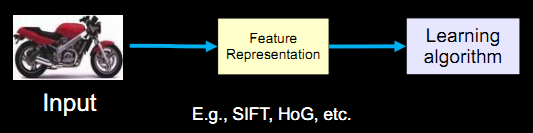
进行特征提取后为：

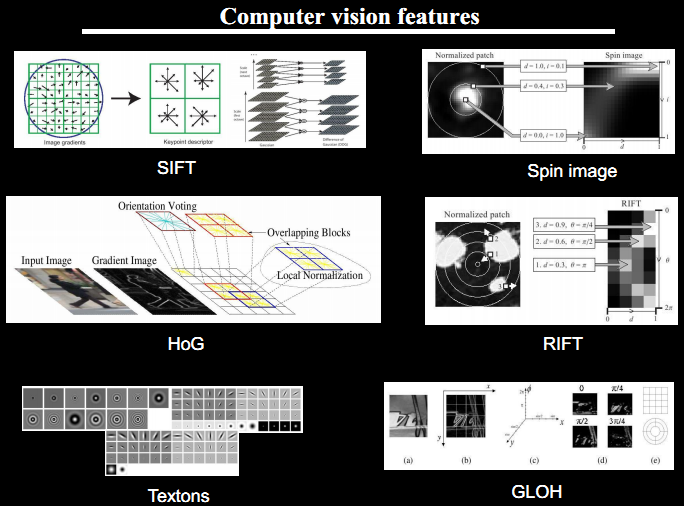
      原始的模式识别是直接对原始图形进行特征提取，而所提取出来的特征和最终的输出很多情况下其实是有冗余成分的，就是说我们只需要关键特征识别就可以，没有必要用那么多特征，更多情况下，那些冗余信息会干扰我们最后的识别结果！

       稀疏编码算法是一种无监督学习方法，它用来寻找一组“超完备”基向量来更高效地表示样本数据。大家对稀疏规则化趋之若鹜的一个关键原因在于它能实现特征的自动选择。一般来说，x_i的大部分元素（也就是特征）都是和最终的输出y_i没有关系或者不提供任何信息的，在最小化目标函数的时候考虑x_i这些额外的特征，虽然可以获得更小的训练误差，但在预测新的样本时，这些没用的信息反而会被考虑，从而干扰了对正确y_i的预测。稀疏规则化算子的引入就是为了完成特征自动选择的光荣使命，它会学习地去掉这些没有信息的特征，也就是把这些特征对应的权重置为0。

2）可解释性(Interpretability)：

       另一个青睐于稀疏的理由是，模型更容易解释。例如患某种病的概率是y，然后我们收集到的数据x是1000维的，也就是我们需要寻找这1000种因素到底是怎么影响患上这种病的概率的。假设我们这个是个回归模型：y=w₁*x₁+w₂*x₂+…+w₁₀₀₀*x₁₀₀₀+b（当然了，为了让y限定在[0,1]的范围，一般还得加个Logistic函数）。

说简单些，logistic函数其实就是这样一个函数：

 

这个函数的曲线如下所示：

 

 

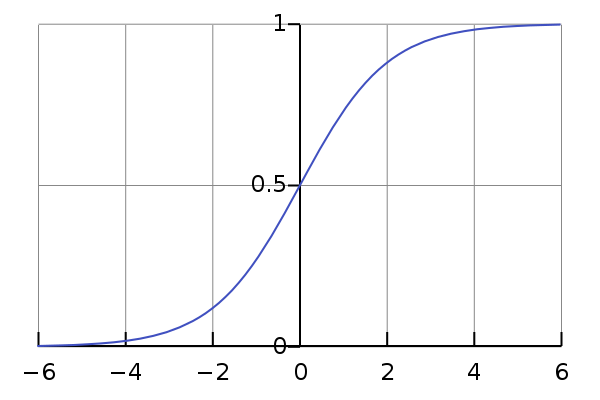
很像一个“S”型吧，所以又叫 sigmoid曲线（S型曲线）。详细的资料可以参考 http://www.cnblogs.com/chaosimple/archive/2013/06/10/3130628.html 

通过学习，如果最后学习到的w*就只有很少的非零元素，例如只有5个非零的w_i，那么我们就有理由相信，这些对应的特征在患病分析上面提供的信息是巨大的，决策性的。也就是说，患不患这种病只和这5个因素有关，那医生就好分析多了。但如果1000个w_i都非0，医生面对这1000种因素，累觉不爱。

本节至此结束，之后会录取更新，同时我的新浪博客有学习记录总结，希望可以和各方学者交流成长http://blog.sina.com.cn/u/2029100307