用BP人工神经网络识别手写数字——《Python也可以》之三
这是我读工程硕士的时候完成课程作业时做的,放在 dropbox 的角落中生尘已经有若干年头了,最近 @shugelee 同学突然来了兴致搞验证码识别,问到我的时候我记起自己做过一点点东西,特发上来给他参考,并趁机补充了一下《Python也可以》系列。
图像预处理
使用下图(后方称为 SAMPLE_BMP)作为训练和测试数据来源,下文将讲述如何将图像转换为训练数据。
灰度化和二值化
在字符识别的过程中,识别算法不需要关心图像的彩色信息。因此,需要将彩色图像转化为灰度图像。经过灰度化处理后的图像中还包含有背景信息。因此,我们还得进一步处理,将背景噪声屏蔽掉,突显出字符轮廓信息。二值化处理就能够将其中的字符显现出来,并将背景去除掉。在一个[0,255]灰度级的灰度图像中,我们取 196 为该灰度图像的归一化值,代码如下:def convert_to_bw(im):
im = im.convert("L")
im.save("sample_L.bmp")
im = im.point(lambda x: WHITE if x > 196 else BLACK)
im = im.convert('1')
im.save("sample_1.bmp")
return im下图是灰度化的图像,可以看到背景仍然比较明显,有一层淡灰色:
下图是二值化的图像,可以看到背景已经完全去除:

图片的分割和规范化:
通过二值化图像,我们可以分割出每一个字符为一个单独的图片,然后再计算相应的特征值,如下图所示: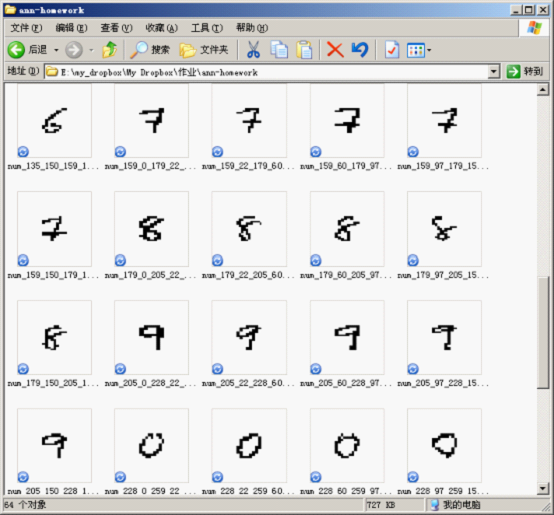
这些图片是由程序自动进行分割而成,其中用到的代码片段如下:
def split(im): assert im.mode == '1' result = [] w, h = im.size data = im.load() xs = [0, 23, 57, 77, 106, 135, 159, 179, 205, 228, w] ys = [0, 22, 60, 97, 150, h] for i, x in enumerate(xs): if i + 1 >= len(xs): break for j, y in enumerate(ys): if j + 1 >= len(ys): break box = (x, y, xs[i+1], ys[j+1]) t = im.crop(box).copy() box = box + ((i + 1) % 10, ) # save_32_32(t, 'num_%d_%d_%d_%d_%d'%box) result.append((normalize_32_32(t, 'num_%d_%d_%d_%d_%d'%box), (i + 1) % 10)) return result其中的 xs 和 ys 分别是横向和竖向切割的分界点,由手工测试后指定,t = im.crop(box).copy() 代码行是从指定的区域中“抠”出图片,然后通过 normalize_32_32 进行规范化。进行规范化是为了产生规则的训练和测试数据集,也是为了更容易地地计算出特征码。
产生训练数据集和测试数据集
为简单起见,我们使用了最简单的图像特征——黑色像素在图像中的分布来进行训练和测试。首先,我们把图像规范化为 32*32 像素的图片,然后按 2*2 分切成 16*16 共 256 个子区域,然后统计这 4 个像素中黑色像素的个数,组成 256 维的特征矢量,如下是数字 2 的一个特征矢量:0 0 4 4 4 2 0 0 0 0 0 0 0 0 2 4 0 0 4 4 4 2 0 0 0 0 0 0 0 0 2 4 2 2 4 4 2 1 0 0 0 0 0 0 1 2 3 4 4 4 4 4 0 0 0 0 0 0 0 0 2 4 4 4 4 4 4 4 0 0 0 0 0 0 0 0 2 4 4 4 4 4 0 0 0 0 0 0 0 0 0 0 2 4 4 4 4 4 0 0 0 0 0 0 0 0 0 0 2 4 4 4 4 4 0 0 0 0 0 0 0 4 4 4 4 4 4 4 4 4 0 0 0 0 0 0 0 4 4 4 4 4 4 4 4 4 2 2 2 2 2 2 2 4 4 2 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 0 2 4 4 4 2 2 2 2 4 3 2 2 2 2 2 0 2 4 4 4 0 0 0 0 4 2 0 0 0 0 0 0 2 4 4 4 0 0 0 0 4 2 0 0 0 0 0 0 2 4 4 4 0 0 0 0 0 0 0 0 0 0 0 0 2 4 4 4 0 0 0 0 0 0 0 0 0 0 0 0 2 4 4 4
相应地,因为我们只需要识别 0~9 共 10 个数字,所以创建一个 10 维的矢量作为结果,数字相应的维置为 1 值,其它值为 0。数字 2 的结果如下:0 0 1 0 0 0 0 0 0 0
我们特征矢量和结果矢量通过以下代码计算出来后,按 FANN 的格式把它们存到 train.data 中去:
f = open('train.data', 'wt')
print >>f, len(result), 256, 10
for input, output in result:
print >>f, input
print >>f, outputBP神经网络
利用神经网络识别字符是本文的另外一个关键阶段,良好的网络性能是识别结果可靠性的重要保证。这里就介绍如何利用BP 神经网络来识别字符。反向传播网络(即:Back-Propagation Networks ,简称:BP 网络)是对非线性可微分函数进行权值训练的多层前向网络。在人工神经网络的实际应用中,80%~90%的模型采用 BP 网络。它主要用在函数逼近,模式识别,分类,数据压缩等几个方面,体现了人工神经网络的核心部分。网络结构
网络结构的设计是根据输入结点和输出结点的个数和网络性能来决定的,如下图。本实验中的标准待识别字符的大小为 32*32 的二值图像,即将 1024 个像素点的图像转化为一个 256 维的列向量作为输入。由于本实验要识别出10 个字符,可以将目标输出的值设定为一个10 维的列向量,其中与字符相对应那个位为1,其他的全为0 。根据实际经验和试验确定,本文中的网络隐含层结点数目为64。因此,本文中的BP 网络的结构为 256-64-10。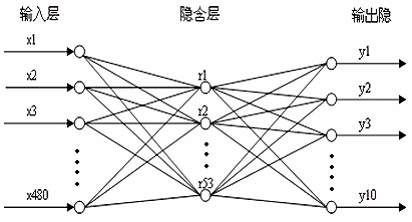
训练结果
本实验中的采用的样本个数为 50 个,将样本图像进行预处理,得到处理后的样本向量P,再设定好对应的网络输出目标向量T,把样本向量 P 和网络输出目标向量 T 都保存到 train.data 文件中。设置好网络训练参数,对网络进行训练和测试,并将最佳的一个网络权值保存到 number_char_recognize.net 文件中。下面就将本文中设置和训练网络参数的程序列举如下:connectionRate = 1 learningRate = 0.008 desiredError = 0.001 maxIterations = 10000 iterationsBetweenReports = 100 inNum= 256 hideNum = 64 outNum=10 class NeuNet(neural_net): def __init__(self): neural_net.__init__(self) neural_net.create_standard_array(self,(inNum, hideNum, outNum)) def train_on_file(self,fileName): neural_net.train_on_file(self,fileName,maxIterations,iterationsBetweenReports,desiredError)可以从代码中看到我们建立起一个输出层有 256 个神经元,隐藏层有 64 个神经元,输出层有 10 个神经元的ANN,其中神经层的连接率为 100%,学习率为 0.28,最大进行 10000 次迭代,并每隔 100 次报告一下学习结果。
if __name__ == "__main__":
ann = NeuNet()
ann.train_on_file("train.data")
ann.save("number_char_recognize2.net")按照上面的程序,对网络进行训练和仿真测试,保存训练性能最好的一组网络权值,并保存到起来。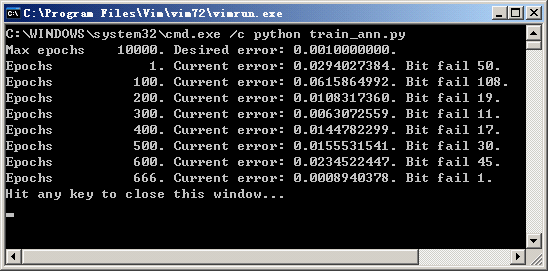
通过 666 次迭代之后,错误率已经低于 0.001,学习中止,并将结果保存起来。
测试结果
实验的测试是通过从保存好的 NN 数据文件中创建 NN 的形式来实验的,具体的代码如下:if __name__ == "__main__":
ann = NeuNet()
ann.create_from_file("number_char_recognize.net")
data = read_test_data()
for k, v in data.iteritems():
k = string_to_list(k)
v = string_to_list(v)
result = ann.run(k)
print euclidean_distance(v, result)
其实 ann.create_from_file 是从文件中读取存档,创建人工神经网络,然后使用 read_test_data 函数读取测试数据,并通过循环对每一个测试数据和相应的期望值转换为 NN 的输入格式,然后使用 ann.run 函数调用神经网络测试,对测试结果与期望值进行欧氏距离计算,对其中的两个测试用例,果如下:
可见两个向量的欧氏距离已经接近于 0,识别效果非常好。





