算法学习笔记（三）问题的转化与高精度运算

问题：设购票点没有任何的零钱，票价50美元，现有m人手持50美元，n人手持100美元，求这样m+n个人构成的队伍有多少种排队方法可以使得整个售票过程不中断。

分析：对于这个问题，经过简单的模拟可以发现，每个手持100的前面必须有一个手持50的，同样如果有k个手持100的连续出现，则前面至少连续k次50。

       这样一来，可以设手持50元的为+1，手持100元的为-1，设ai为为第i个人所对应的值，则问题转化为数组的部分和a1+a2+...+ak≥0，其中k≤m+n，为了求这样的数列的个数，需要使用组合数学的相关知识，这个问题可以使用现成的结论，第n个Catalan数，公式为：

      

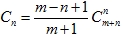
       在运算时，要特别注意m＜n的情况，在这种情况下，无法满足要求。

算法实现：由于购票人数一般很多，这就带来了高精度运算的问题，不再能使用传统的运算方式。高精度运算的一种方法是把数据都转化为字符串，再对字符串定义运算。

   ①将数据转化为字符串

   将数据转化为字符串的算法是十分有效的，尤其在单片机的编程当中，一般的算法是将整数从高位到低位顺次存入一个字符数组，这时字符数组所存的数据是反的，这时候需要再设定一个数组将其反过来，通过查阅资料，发现了一种比较号的算法，它的亮点是①充分利用i++的先运算后++特性简化代码，②省略对位数的判断，而采用while(n)判断所有位数是不是都已经取完，③在字符数组尾部赋0从而保证字符串在最后一个有效位后结束。代码如下：

void NumToString(int n, char* s)
{
    int i,j,temp[8]; //临时数组，先把数位存入其中，倒序
    if(n == 0)
    {
        s[0] = '0';
        s[1] = 0; //在有效位之后添加\0
        return;
    }
    i = 0;
    while(n) //判断有没有取完所有位
    {
        temp[i++] = n % 10; //先存入，后i++
        n /= 10;
    }
    i -= 1;
    j = 0;
    while(i >= 0)
        s[j++] = temp[i--] + '0'; //将倒序的数组正序存入s数组，s数组存有最终结果
    s[j] = 0;
}

    ②重新定义字符串的运算，以乘法为例，算法如下：

void mul(char* m, char* n, char* res)
{
    int i,j,len1,len2;
    len1 = strlen(m);
    len2 = strlen(n);
    int *r = new int[len1 + len2 + 1]; //乘积的长度，例如两位乘以两位，最多为5位，因此多加1
    for(i = 0; i <= len1 + len2; i++) r[i] = 0; //初始化乘积存储数组
    for(i = 0; i < len1; i++)
        for(j = 0; j < len2; j++)
            r[i + j + 1] += (m[i] - '0')*(n[j] - '0'); //依次从最高位、次高位直至最低位进行运算，注意，这里的最高位实际为次高位，因为
                                                       //真正的最高位只能通过进位获得，而不是通过乘运算
    for(i = len1 + len2 - 1; i >=1; i--) //从最低位开始处理进位
    {
        if(r[i] > 9) 
        {
            int temp = r[i] / 10; //储存进位数
            r[i] %= 10; //将进位后的数组存在这一位
            r[i-1] += temp; //进位运算，同时处理r[0]这一位（进位可能到达的最高位，没有则为0）
        }
    }
    for(i = 0; i<len1+len2;i++) cout << r[i] << " ";
    cout << endl;
    //经过这样的运算，将会得到数据字符串，其中最高位在r[0]内，最低位在r[len1+len2-1]内
    for(i = 0; i < len1+len2; i++) //判断是否乘积为0，为0则i会自加到len1+len2
        if(r[i] != 0) break;
    if(i == len1 + len2)
    {
        res[0] = '0';
        res[1] = 0;
        return;
    }
    //如果乘积不为0，会进行下面的运算，顺次将r[0]到r[len1+len2-1]存入res[0]到res[len1+len2-1]
    j = 0;
    while(i < len1 + len2)
    {
        res[j++] = r[i++] + '0';
    }
    res[j] = 0;
    delete[] r;
}