朴素贝叶斯算法
朴素贝叶斯算法
-
简介:朴素贝叶斯算法是一种基于概率统计的分类方法。在条件独立假设的基础上,使用贝叶斯定理构建算法,在文本处理中广泛使用
-
优点:在数据较少的情况下仍然有效,可以处理多分类问题
-
-
适用类型:标称型数据。标称型数据是指标称型目标变量的结果只在有限目标集中取值,如真与假或者只存在是与否(标称型目标变量主要用于分类)
-
贝叶斯公式
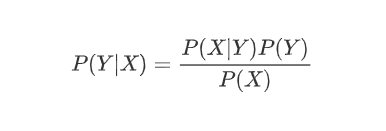
-
知识扩展
在条件概率中,已知事件B出现的条件下A出现的概率,称为条件概率,记作P(A|B)
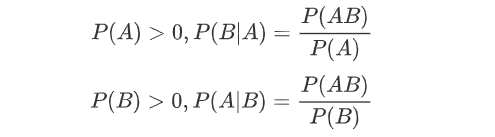
很明显,贝叶斯公式的推导由此而生
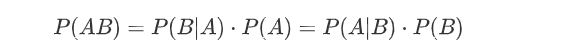
-
-
朴素贝叶斯公式:但是在条件独立的情况下,将X分割成X1,X2,X3,....,那么朴素贝叶斯公式就是朴素贝叶斯公式

-
词袋模型:详细解释朴素贝叶斯公式
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 X1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 X2 S M M S S S M M L L L M M L L Y -1 -1 1 1 -1 -1 -1 1 1 1 1 1 1 1 -1 -
问题:给定的x=(2, S)是属于哪种类别
-
计算先验概率
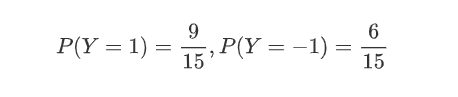
-
计算各种条件概率
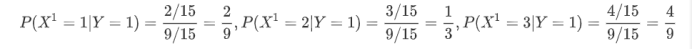
-
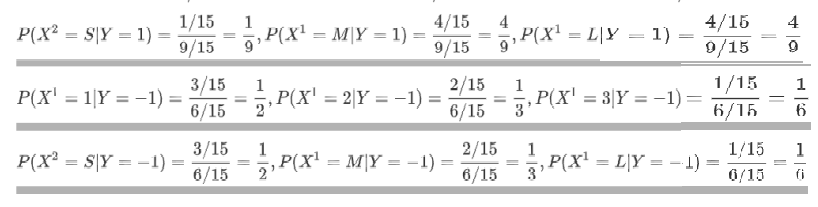
-
对于给定的x=(2, S),计算
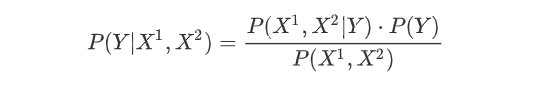
由于分母相同,暂不计算,当Y分别等于1和-1
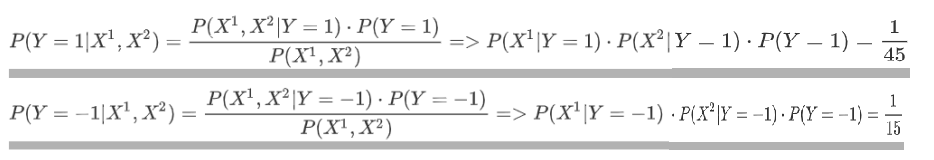
-
根据值的大小判定类别,x=(2, S)属于-1
-
-
朴素贝叶斯的三种模型
-
多项式模型:当特征是离散的时候,使用多项式模型。多项式模型在计算先验概率,P(yk)和条件概率P(xi|yk)时,会做一些平滑处理,该模型常用于文本分类,具体公式
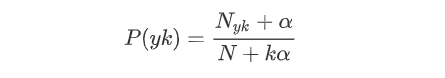
N是总体样本个数,k是总的类别个数,Nyk是类别为yk样本个数,α是平滑值
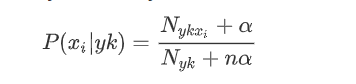
Nyk是类别为yk的样本个数,n是特征的维数,Nykxi是类别为yk的样本中,第i维特征的值是xi的样本个数,α是平滑值。当α=1时,称作Laplace平滑,0<α<1时,称作Lidstone平滑,当α=0时,不做平滑,但是如果不做平滑,当某一维特征值xi没在训练样本中出现过时,会导致P(xi|yk)=0,从而后验概率为0,加上平滑可以克服这个问题。
-
伯努利模型:在伯努利模型中,对于一个样本来说,其特征用的是全局的特征。而且每个特征值都是布尔类型。在文本分类中,就是一个特征在文本中是否出现过。如果特征值xi=1
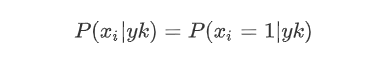
如果特征值xi=0
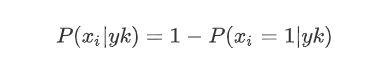
这就意味着 “ 没有某个特征 ” 也是一个特征
-
混合模型:
-
-
-
编码实现
import numpy as np class MyBayes: def __init__(self): # 文本数据集,数据可修改 self.trainData = [ # 每一个列表表示文本中的一行 ["my", "dog", "has", "flea", "problems", "help", "please"], ["maybe", "not", "take", "him", "to", "dog", "park", "stupid"], ["my", "dalmation", "is", "so", "cute", "I", "love", "him"], ["stop", "posting", "stupid", "worthless", "garbage"], ["mr", "licks", "ate", "my", "steak", "how", "to", "stop", "him"], ["quit", "buying", "worthless", "dog", "food", "stupid"], ] # 对应标签,数据可修改 self.labels = [0, 1, 0, 1, 0, 1] # 定义一个词条列表 self.vocabList = self.create_vocabulary_list() # 定义一个词条向量矩阵 self.vectorMatrix = self.words_to_vec() def create_vocabulary_list(self): """ 构建词条集,将trainData中出现过的所有单词构建一个集合 :return: vocabSet: 词条集合,包含dataSet出现过的单词 """ vocab = set([]) for document in self.trainData: # 返回前后集合的并集 vocab = vocab | set(document) return list(vocab) def words_to_vec(self): """ 文本转换向量矩阵 :return: 二维列表 """ vector_matrix = [self.word_to_vec(words) for words in self.trainData] return vector_matrix def word_to_vec(self, words): """ 文本中的一行转换向量矩阵 使用伯努利模型将数据进行数值化转换,构建一个与vocabList大小一致的数值列表 扫描inputSet,如果inputSet中的单词出现在vocabList中则数值列表对应的位设置为1,否则为0 :param words: 一句话中单词组成的单词列表 :return: vec数值化后0,1组成的列表 """ vec = [0]*len(self.vocabList) for word in words: if word in self.vocabList: vec[self.vocabList.index(word)] = 1 else: print("The word '{}' is not in my vocabulary!".format(word)) return vec def naive_bayes_cal(self): """ 朴素贝叶斯计算 计算所有类别概率 计算每个类别下每个词条出现的条件概率 为防止向下溢出(多个小于1的概率相乘四舍五入为0),结果采用对数(乘法变加法)计算 0表示正常性评论,1表示简单性评论 :return: p0Vec: 所有分类为0的文本中每个词条出现的条件概率 p1Vec: 所有分类为1的文本中每个词条出现的条件概率 pAbusive: 分类为1的文本的概率 """ # 文档总数,词条总数 doc_nums, word_nums = len(self.vectorMatrix), len(self.vectorMatrix[0]) # 简单性评论概率 p_abusive = sum(self.labels) / float(doc_nums) # 正常性、简单性评论词频统计 p0_num, p1_num = np.ones(word_nums), np.ones(word_nums) # 正常性、简单性评论中出现的总词条数,作为计算条件概率的分母 p0_sum, p1_sum = 2.0, 2.0 for i in range(doc_nums): if self.labels[i] == 0: p0_num += self.vectorMatrix[i] p0_sum += sum(self.vectorMatrix[i]) else: p1_num += self.vectorMatrix[i] p1_sum += sum(self.vectorMatrix[i]) p0_vec = np.log(p0_num / p0_sum) p1_vec = np.log(p1_num / p1_sum) return p0_vec, p1_vec, p_abusive def naive_bayes_classify_global(self): """ 分类测试,测试文本所有行 :return: """ d = {str(self.trainData[i]): self.naive_bayes_classify(self.vectorMatrix[i]) for i in range(len(self.labels))} for key, value in d.items(): print("{} res is {}".format(key, value)) def naive_bayes_classify(self, word): """ 分类测试 :param word: 测试文本中的一行 :return: 类别为0或者1 """ p0_vec, p1_vec, p_class1 = self.naive_bayes_cal() p0 = sum(word*p0_vec) + np.log(1-p_class1) p1 = sum(word*p1_vec) + np.log(p_class1) return 1 if p1 > p0 else 0 if __name__ == '__main__': my_bayes = MyBayes() # my_bayes.naive_bayes_classify_global() doc = ["how", "to", "stop", "him", "my", "steak", "dog"] docVec = my_bayes.word_to_vec(doc) res = my_bayes.naive_bayes_classify(docVec) print("{} is {}".format(doc, res))


