AVL树到底是什么？

 一. 什么是AVL树

在认识AVL树之前我们先认识一下什么是二叉搜索树:

1.二叉搜索树

二叉搜索树又称为二叉排序树,二叉搜索树满足所有的左孩子节点都小于其根节点的值,所有的右孩子节点都大于其根节点的值,二叉搜索树上的每一棵子树都是一棵二叉搜索树,因此二叉搜索树通过中序遍历可以获得一个有序的序列(由小到大);

 

 

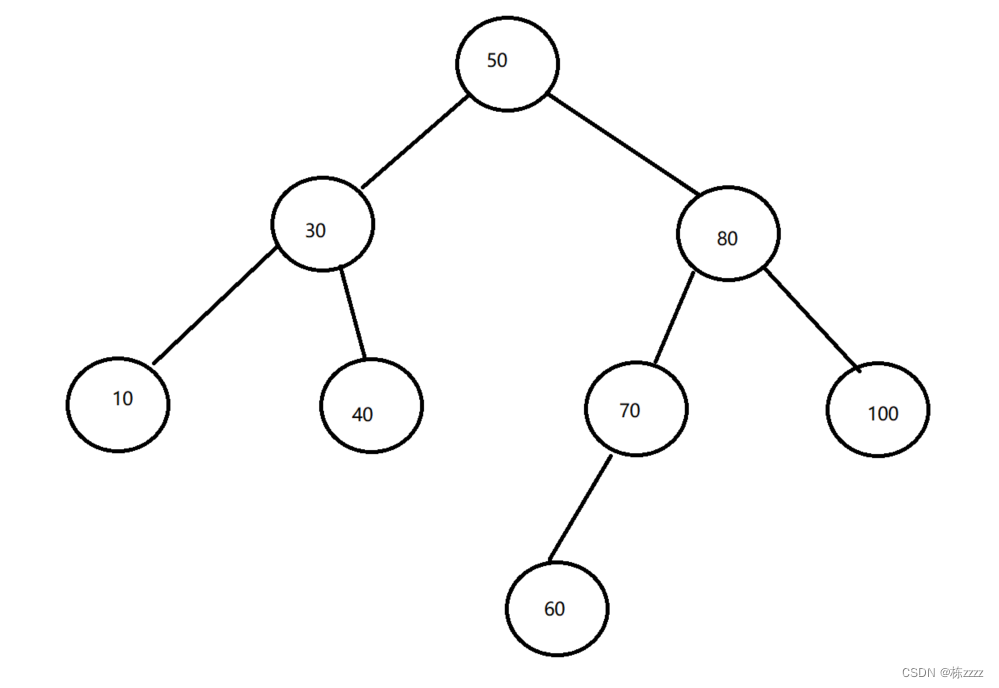
类似于这样的树就是一棵二叉搜索树;

2.为什么引入了AVL树

二叉搜索树看似很美好,但其却有一些缺陷.对于二叉搜索树而言,是和查找相关的，而不论是查找还是删除,都需要先进行查找,也就是对整棵树来进行遍历,而对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度函数,也就是结点越深，则比较次数越多.最优的情况下是：二叉搜索树为完全二叉树，其平均比较次数为：l o g 2 n log_2{n}log
2
​
n,但是如果二叉搜索树退化成了一棵单分支的树,其平均比较次数为：n/2,就是最差的情况了

这就相当于是一个顺序表的查找了,这样二叉搜索树的优势就完全消失了,因此就引入了AVL树!

3.什么是AVL树
AVL树又称自平衡二叉查找树,是高度平衡的二叉搜索树,就是在二叉搜索树的基础上进行了优化,既当向二叉搜索树中插入新结点后，保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),也就是降低树的高度,这样就可以减少平均搜索长度了,因此AVL树满足它的左右子树都是AVL树,左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1),这就是AVL树的优势所在,因此如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在 ，搜索时间复杂度O(l o g 2 n log_2{n}log

平衡因子 = 右子树的高度 - 左子树的高度

二. 自己构造AVL树

这里的构造还是和二叉搜索树的构造差不多的，只不过在这里插入元素的话就需要考虑平衡因子的事情了，因为一定要保证插入元素后此树还是一棵AVL树，就需要进行相关调整，这里就先不过多介绍了，下面再详细介绍，先来构造一棵简单的AVL树：

public class AVLTree {
    static class TreeNode{
        //内部类，表示AVL树的每个节点

        //val值
        public int val;
        //左孩子的引用
        public TreeNode left;
        //右孩子的引用
        public TreeNode right;
        //父亲节点的引用
        public TreeNode parent;
        //平衡因子(每个节点都有）
        public int bf;
        public TreeNode(int val){
            this.val = val;
        }
    }

    //根节点
    public TreeNode root;
    public boolean insert(int val){
       
    }
}

这样一棵简单的AVL树就构造好了，下面就来写一下AVL树的插入！

三. AVL树的插入和删除

1.插入

首先就是将节点插进来，和二叉搜索树一样，先只看位置在哪，不关注平衡因子

这个为要插入节点：

   TreeNode node = new TreeNode(val);
        if(root == null){
            //没有根节点，要插入的就是根节点
            root = node;
            return true;
        }
        //记录每个节点的父节点
        TreeNode parent = null;
        //要移动的代节点
        TreeNode cur = root;
        //根据val的值和root进行比较来确定应该插入节点的位置
        while (cur != null){
            if(cur.val > val){
                //大于证明此节点应在左子树
                parent = cur;
                cur = cur.left;
            }else if(cur.val < val){
                //大于证明此节点应在右子树
                parent = cur;
                cur = cur.right;
            }else {
                //不能有值一样的节点
                return false;
            }
        }
        //此时cur为空，需要找到对应的位置
        if(parent.val > val){
            parent.left = node;
        }else{
            parent.right = node;
        }

此时节点就已经插进来了，此时就需要看其每个节点的平衡因子了

        //而此时就需要对树进行平衡因子的调整了，保证树是高度平衡的
        //再反着回去写
        node.parent = parent;
        cur = node;
        //当父亲节点一直存在的时候，就表示没有调到根节点就需要继续调整
        while(parent != null){
            if(cur == parent.right){
                //在右边右树高度加一，因此bf+1
                parent.bf++;
            }else{
                //再左边，左树高度加一，因此bf-1
                parent.bf--;
            }
            //在这里就要进行判断了，如果此时的父亲节点如果平衡因子为0了，那么就不需要再往上走了，因为上面的都是平衡的
	        if(parent.bf == 0){
	            return true;
	        }else if(parent.bf == -1 || parent.bf == 1){
	            //此时父亲节点的平衡因子为1、-1
	             //此时表示当前树平衡了，但是不表示整棵树都平衡了，因此还需要继续往上走
	            cur = parent;
	            parent = cur.parent;
	        }else{
	            //此时父亲节点的平衡因子为2、-2
	            if(parent.bf == 2){
                //此时右树高 需要降低右树的高度
	                if(cur.bf == 1){
	                    //左单旋
	                    rotateLeft(parent);
	                }else{
	                    //右左双旋
	                    rotateRL(parent);
	                }
	            }else{
	                //此时左树高，需要降低左树的高度
	                if(cur.bf == 1){
	                    //左右双旋
	                    rotateLR(parent);
	                }else{
	                    //右单旋
	                    rotateRight(parent);
	                }
	            }
	            //调整完就平衡了
	            break;
	        }
        }