一 栈和队列介绍
1 栈
堆是在程序运行时,而不是在程序编译时,申请某个大小的内存空间。即动态分配内存,对其访问和对一般内存的访问没有区别。堆是指程序运行时申请的动态内存,而栈只是指一种使用堆的方法(即先进后出)。
栈(stack)——先进后出,删除与加入均在栈顶操作
栈也称为堆栈,是一种线性表。
堆栈的特性: 最先放入堆栈中的内容最后被拿出来,最后放入堆栈中的内容最先被拿出来, 被称为先进后出、后进先出(FILO—First-In/Last-Out)。
2 队列
队列和栈不同的是,队列是一种先进先出(FIFO—first in first out)的数据结构。

3 Deque
Deque的含义是“double ended queue”,即双端队列,它既可以当作栈使用,也可以当作队列使用。
下表列出了Deque与Queue相对应的接口:
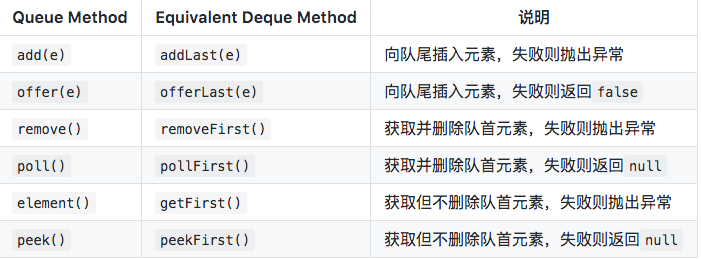
下表列出了Deque与Stack对应的接口:

4 ArrayDeque
从名字可以看出ArrayDeque底层通过数组实现,为了满足可以同时在数组两端插入或删除元素的需求,该数组还必须是循环的,即循环数组(circular array),也就是说数组的任何一点都可能被看作起点或者终点。
ArrayDeque是非线程安全的(not thread-safe),当多个线程同时使用的时候,需要程序员手动同步;另外,该容器不允许放入null元素。
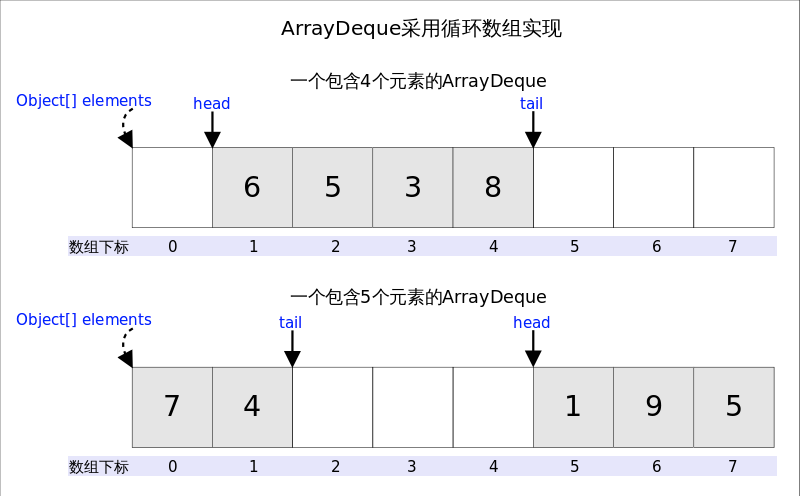
head指向首端第一个有效元素,tail指向尾端第一个可以插入元素的空位。因为是循环数组,所以head不一定总等于0,tail也不一定总是比head大。
addFirst()
针对首端插入实际需要考虑:1.空间是否够用,以及2.下标是否越界的问题。上图中,如果head为0之后接着调用addFirst(),虽然空余空间还够用,但head为-1,下标越界了。下列代码很好的解决了这两个问题。
public void addFirst(E e) { if (e == null) throw new NullPointerException(); //下标越界问题解决方案 elements[head = (head - 1) & (elements.length - 1)] = e; //容量问题解决方案 if (head == tail) doubleCapacity(); }
addLast()
addLast(E e)的作用是在Deque的尾端插入元素,也就是在tail的位置插入元素,由于tail总是指向下一个可以插入的空位,因此只需要elements[tail] = e;即可。插入完成后再检查空间,如果空间已经用光,则调用doubleCapacity()进行扩容。与first比较类似就不多分析了.

二 使用两个队列实现栈
1 描述
使用队列实现栈的下列操作:
push(x) -- 元素 x 入栈
pop() -- 移除栈顶元素
top() -- 获取栈顶元素
empty() -- 返回栈是否为空
注意:
你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
你所使用的语言也许不支持队列。 你可以使用 list 或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
你可以假设所有操作都是有效的(例如, 对一个空的栈不会调用 pop 或者 top 操作)。
2 思路
起初的时候,两个队列都是空的,那么当“栈”要压入一个元素,我们就默认将该元素压入到队列1中。接下来继续压入剩余的元素。
接下来考虑,如果我们想要弹出一个元素如何操作。栈中要求出栈的为栈顶元素,那么即为最后插入的元素,但是该元素在队列的尾部,必须要求前面的元素出队后才能访问,说到这里,你也就发现思路的:出队前面的元素,到另一个队列中,那么就可以在原队列中弹出唯一的元素了。
现在我们再考虑另一个情况,队列里面还有元素,“栈”又进来了新的元素,那么就将新元素,压入到存在元素的那一个队列中,剩余的操作,上面已经提到了,一样的操作,看图也许就清晰多了。

3 代码实现

public class MyStack { Queue<Integer> queueOne;//用来存放数据 Queue<Integer> queueTwo;//用来辅助 /** * 初始化队列 */ public MyStack() { queueOne = new LinkedList<>(); queueTwo = new LinkedList<>(); } /** * 数据入栈 */ public void push(int x) {//从队列1中加入元素 queueOne.add(x); } /** * 出栈,删除并返回栈顶元素 */ public int pop() { if (queueOne.isEmpty() && queueTwo.isEmpty()) { return -1; } if (queueTwo.isEmpty()) {//如果队列2为空 while (queueOne.size() > 1) {//把队列1中的元素依次出对列并加入到2中 int temp = queueOne.poll(); queueTwo.add(temp); } return queueOne.poll();//弹出队列1的最后一个元素 } else {//如果队列2不为空 if (!queueOne.isEmpty()) {//如果队列1不为空,重复上面的操作 while (queueOne.size() > 1) { int temp = queueOne.poll(); queueTwo.add(temp); } return queueOne.poll(); } else { while (queueTwo.size() > 1) { int temp = queueTwo.poll(); queueOne.add(temp); } return queueTwo.poll(); } } } /** * 返回栈是否为空 */ public boolean empty() { return queueOne.isEmpty() && queueTwo.isEmpty(); } }
三 使用两个栈实现一个队列
1 描述
用栈的入栈和出栈来实现队列的入队和出队:
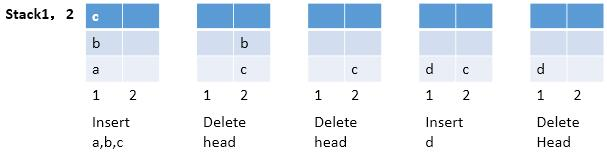
stack1是入栈的,stack2是出栈的。
入队列:直接压入stack1即可
出队列:如果stack2不为空,把stack2中的栈顶元素直接弹出;
否则,把stack1的所有元素全部弹出压入stack2中,再弹出stack2的栈顶元素
2 思路
起初的时候,两个栈都为空,那么只要有元素来,那么默认插入到第一个栈。这时如果要求删除一个元素,那么元素已经不在栈顶,在第一个栈中肯定无法直接删除了,此时我们发现第二个栈还没有派上用场,这里用到了,把第一个栈中的元素压入到第二个栈中,可以发现原来在第一个栈中栈底的元素已经出现在第二个栈的栈顶上,所以删除的功能就实现了。如果这个时候,“队列”里还有元素,我们还可以继续出队,而且,现在要出队的元素就在第二个栈的栈顶,所以直接出栈即可。
分析到现在,下面给出总结:如果栈2不为空,同时又需要出队,那么顺其自然直接弹出即可。如果栈2为空,那么从栈1中逐个弹出压入,那么完整的实现了先进先出的功能。
3 代码实现

public class Stack2Queue { /** * 用栈的入栈和出栈 * 来实现队列的入队和出队 * stack1是入栈的,stack2是出栈的。 * 入队列:直接压入stack1即可 * 出队列:如果stack2不为空,把stack2中的栈顶元素直接弹出; * 否则,把stack1的所有元素全部弹出压入stack2中,再弹出stack2的栈顶元素 */ Stack stack1 = new Stack(); Stack stack2 = new Stack(); public void add(Object o) { stack1.push(o); } public Object poll() { Object o = null; if (stack2.size() == 0) { //把stack1的数据放入stack2,留下最后一个数据 while (stack1.size() > 1) { stack2.push(stack1.pop()); } if (stack1.size() == 1) { //把stack1的留下的那个数据返回出去 o = stack1.pop(); } } else {//如果stack2不为空,则直接弹出栈顶 o = stack2.pop(); } return o; } public int length() { return stack1.size() + stack2.size(); } }



