hihocoder 1158 质数相关 dp

描述

两个数a和 b (a<b)被称为质数相关，是指a × p = b，这里p是一个质数。一个集合S被称为质数相关，是指S中存在两个质数相关的数，否则称S为质数无关。如{2, 8, 17}质数无关，但{2, 8, 16}, {3, 6}质数相关。现在给定一个集合S，问S的所有质数无关子集中，最大的子集的大小。

输入

第一行为一个数T，为数据组数。之后每组数据包含两行。

第一行为N，为集合S的大小。第二行为N个整数，表示集合内的数。

输出

对于每组数据输出一行，形如"Case #X: Y"。X为数据编号，从1开始，Y为最大的子集的大小。

数据范围

1 ≤ T ≤ 20

集合S内的数两两不同且范围在1到500000之间。

小数据

1 ≤ N ≤ 15

大数据

1 ≤ N ≤ 1000

样例输入

3
5
2 4 8 16 32
5
2 3 4 6 9
3
1 2 3

样例输出

Case #1: 3
Case #2: 3
Case #3: 2

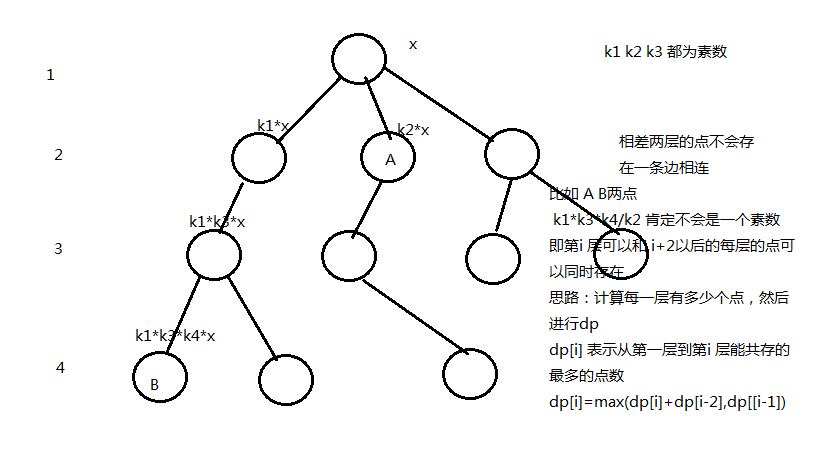
#include<string.h>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<malloc.h>
#include<time.h>
#include<cmath>
#include<algorithm>
#include<vector>
#include<queue>
#include<cstdlib>
#include<set>
#include<map>
using namespace std;
typedef  long long LL;
#define kmax 500000
LL prim[kmax+100],cnt,vit[kmax+100];
LL p[1010],n;
map<LL,LL>lk;
vector<LL>ko[kmax+100];
LL deep[1010],dp[1010];
void getprim(){
    cnt=0;
    memset(vit,0,sizeof(vit));
    for(LL i=2;i<=kmax;i++){
        if(!vit[i]){
            prim[++cnt]=i;
        }
         for(LL j=1;j<=cnt&&prim[j]*i<=kmax;j++){
              vit[prim[j]*i]=1;
              if(i%prim[j]==0) break;
            }
    }
}
void bfs(LL pos){
    int sum=0;
    queue<LL>tmp;
    while(!tmp.empty()) tmp.pop();
    tmp.push(p[pos]);
    while(!tmp.empty()){
        LL to=tmp.front(),pe=deep[lk[to]];tmp.pop();vit[to]=0;
        for(LL i=0;i<ko[to].size();i++){
            LL num=ko[to][i];
            if(vit[num]) {
                deep[lk[num]]=pe+1;
                tmp.push(num);
            }
        }
        sum++;
    }
}
LL getans(LL pos){
    if(ko[p[pos]].size()==0) return 1; // 这个数可以与任何一个数同时存在
    LL mmax=1;
    memset(deep,0,sizeof(deep));
    memset(dp,0,sizeof(dp));
    deep[pos]=1;
    bfs(pos);   // 求与 p[pos] 这个数有边的数 deep 值
    for(LL i=0;i<n;i++) if(deep[i]) dp[deep[i]]++,mmax=max(mmax,deep[i]);// 舒适化dp
    for(LL i=2;i<=mmax;i++) dp[i]=max(dp[i]+dp[i-2],dp[i-1]);
    return dp[mmax];
}
int main(){
    getprim();
    LL t,cas=0;cin>>t;
    while(t--){
        cin>>n;
        memset(vit,0,sizeof(vit));
        for(LL i=0;i<n;i++) cin>>p[i],ko[p[i]].clear(),vit[p[i]]=1;lk.clear();
        sort(p,p+n);
        for(LL i=0;i<n;i++) lk[p[i] ]=i;
        /* 给质数相关的数建边*/
        for(LL j=0;j<n;j++){
            for(LL k=1;k<=cnt;k++){
                if(1ll*p[j]*prim[k]>p[n-1]) break;
                if(vit[p[j]*prim[k]]){
                    ko[p[j] ].push_back(p[j]*prim[k] );
                    ko[p[j]*prim[k]].push_back(p[j]);
                }
            }
        }
        LL ans=0;
        for(LL i=0;i<n;i++)
        if(vit[p[i]]){
            ans+=getans(i);
        }
        printf("Case #%lld: %lld\n",++cas,ans);
    }
}