数学:二项式定理
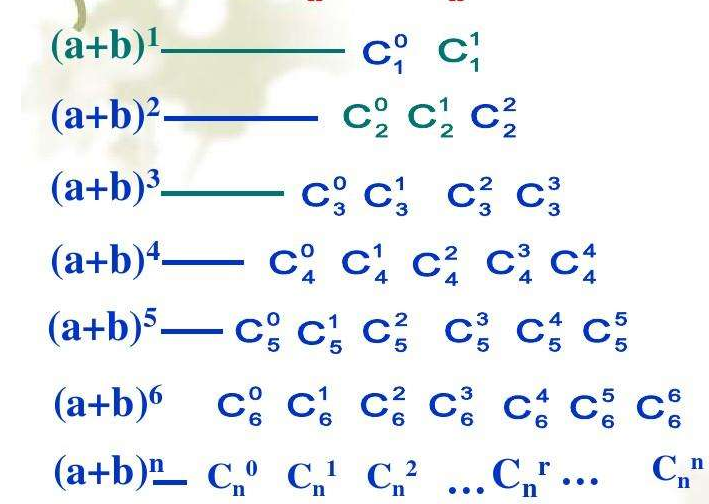
先贴一张网图来弥补一下知识点,回顾NOIP2011计算系数
既然我们要求的是展开式中某一项的系数,那么就直接求出其对应的组合数就好了,但是要注意x和y都是有系数a和b的
x,y换成ax,by,得到x^ny^m的系数是a^n*b^m*C(k,n)
这样就可以了
在计算幂的时候可以优化的,NOIP签到题当然就不用了
1 #include<cstdio> 2 const int maxn=1005; 3 const int mod=10007; 4 int a,b,k,n,m,ans; 5 int f[maxn][maxn]; 6 int main() 7 { 8 scanf("%d%d%d%d%d",&a,&b,&k,&n,&m); 9 a=a%mod;b=b%mod; 10 for(int i=1;i<=k;i++) {f[i][i]=f[i][0]=1;f[i][1]=i;} 11 for(int i=3;i<=k;i++) 12 for(int j=2;j<i;j++) 13 f[i][j]=(f[i-1][j]+f[i-1][j-1])%mod; 14 ans=f[k][m]%mod; 15 for(int i=1;i<=n;i++) ans=(ans*a)%mod; 16 for(int i=1;i<=m;i++) ans=(ans*b)%mod; 17 printf("%d",ans); 18 return 0; 19 }
组合数学博大精深,与程序设计联系紧密,其离散的性质可谓是考察的玄学。。
有空总结一下排列组合的全部内容,补一下高中欠下的坑



