Geatpy学习笔记1：官方案例
一、入门
1、求解器模式入门
案例 1
import geatpy as ea
import numpy as np
# 构建问题
r = 1 # 目标函数需要用到的额外数据
@ea.Problem.single
def evalVars(Vars): # 定义目标函数（含约束）
f = np.sum((Vars - r) ** 2) # 计算目标函数值
x1 = Vars[0]
x2 = Vars[1]
CV = np.array([(x1 - 0.5)**2 - 0.25,
(x2 - 1)**2 - 1]) # 计算违反约束程度
return f, CV
problem = ea.Problem(name='soea quick start demo',
M=1, # 目标维数
maxormins=[1], # 目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标
Dim=5, # 决策变量维数
varTypes=[0, 0, 1, 1, 1], # 决策变量的类型列表，0：实数；1：整数
lb=[-1, 1, 2, 1, 0], # 决策变量下界
ub=[1, 4, 5, 2, 1], # 决策变量上界
evalVars=evalVars)
# 构建算法
algorithm = ea.soea_SEGA_templet(problem,
ea.Population(Encoding='RI', NIND=20),
MAXGEN=50, # 最大进化代数。
logTras=1, # 表示每隔多少代记录一次日志信息，0表示不记录。
trappedValue=1e-6, # 单目标优化陷入停滞的判断阈值。
maxTrappedCount=10) # 进化停滞计数器最大上限值。
# 求解
res = ea.optimize(algorithm, seed=1, verbose=True, drawing=1, outputMsg=True, drawLog=False, saveFlag=True, dirName='result')
分析
- 从上述代码可见，我们可以先定义一个目标函数，然后创建问题，再是构建算法，最后调用optimize()函数求解。 在上面的例子中，我们在定义目标函数时，加了一个@ea.Problem.single的标记。它可以让目标函数evalVars()的传入参数是一个Numpy ndarray类型的一维数组，它的实际含义是种群的某个个体对应的决策变量。在evalVars()中，我们通过f=np.sum((Vars - r) ** 2)计算出这组决策变量对应的目标函数值。
- 然后通过CV = np.array([(x1 - 0.5)2 - 0.25, (x2 - 1)2 - 1])来计算违反约束程度值。这是因为该问题除了变量范围外，有2个不等式约束。如果(x1−0.5)2−0.25的值大于0，就说明违反了(x1−0.5)2 \le 0.25的约束，并且(x1−0.5)^2的值越大，违反约束的程度就越大。我们把计算得到的两个约束的违反约束程度值拼合在一起组成一个一维数组，就得到一个数组表示这组决策变量所有的违反约束程度值。
- 代码的第15行，这里调用了Geatpy的Problem问题类的构造函数，得到一个问题对象。 其中maxormins是一个记录着各个目标函数是最小化抑或是最大化的Numpy array行向量，其中元素为1表示对应的目标是最小化目标；为-1表示对应的是最大化目标。例如M=3，maxormins=array([1,-1,1])，此时表示有三个优化目标，其中第一、第三个是最小化目标，第二个是最大化目标。varTypes是一个记录着决策变量类型的行向量，其中的元素为0表示对应的决策变量是连续型变量；为1表示对应的是离散型变量。
- 接着，第24行，我们实例化了Geatpy内置实现的一个进化算法类的对象。其中第25行定义了该进化算法用什么样的种群去进化。Encoding='RI'表示改种群的染色体是'RI'编码，即“实数整数混合编码”，简称“实整数编码”。类似的还有'P'编码（排列编码，可以让对应的变量互不相同）、'BG'编码（二进制/格雷码编码）。然后NIND=20设定了种群有20个个体。
- 最后，在第31行，调用geatpy的optimize()函数进行求解。其中seed=1表示设置随机数种子。如果不想设置随机数种子，则把它设为None，或者不把它传入到optimize()函数中。dirName='result'表示把求解结果以文件的形式保存在当前工作目录下的result文件夹中。如果不传入dirName或者设dirName为None，则默认会以求解的起始时间的信息作为文件夹，把结果保存在里面。optimize()函数的其他传入参数以及31行获得的返回值res（类型为python字典）的内容可以用help(ea.optimize)或跳转进入源码查看。例如res['ObjV']表示算法搜索到的最佳目标函数值（它是个Numpy ndarray二维数组，每一行表示一组目标函数值。）；res['Vars']表示对应的决策变量值矩阵（Numpy ndarray二维数组，每一行表示一组决策变量值）。
help(ea.optimize)
optimize(algorithm, seed=None, prophet=None, verbose=None, drawing=None, outputMsg=True, drawLog=True, saveFlag=True, dirName=None, **kwargs)
描述: 该函数用于快速部署问题和算法，然后对问题进行求解。
输入参数:
algorithm : <class: class> - 算法类的引用。
seed : int - 随机数种子。
prophet : <class: Population> / Numpy ndarray - 先验知识。可以是种群对象，
也可以是一组或多组决策变量组成的矩阵（矩阵的每一行对应一组决策变量）。
verbose : bool - 控制是否在输入输出流中打印输出日志信息。
该参数将被传递给algorithm.verbose。
如果algorithm已设置了该参数的值，则调用optimize函数时，可以不传入该参数。
drawing : int - 算法类控制绘图方式的参数，
0表示不绘图；
1表示绘制最终结果图；
2表示实时绘制目标空间动态图；
3表示实时绘制决策空间动态图。
该参数将被传递给algorithm.drawing。
如果algorithm已设置了该参数的值，则调用optimize函数时，可以不传入该参数。
outputMsg : bool - 控制是否输出结果以及相关指标信息。
drawLog : bool - 用于控制是否根据日志绘制迭代变化图像。
saveFlag : bool - 控制是否保存结果。
dirName : str - 文件保存的路径。当缺省或为None时，默认保存在当前工作目录的'result of job xxxx-xx-xx xxh-xxm-xxs'文件夹下。
输出参数:
result : dict - 一个保存着结果的字典。内容为：
{'success': True or False, # 表示算法是否成功求解。
'stopMsg': xxx, # 存储着算法停止原因的字符串。
'optPop': xxx, # 存储着算法求解结果的种群对象。如果无可行解，则optPop.sizes=0。optPop.Phen为决策变量矩阵，optPop.ObjV为目标函数值矩阵。
'lastPop': xxx, # 算法进化结束后的最后一代种群对象。
'Vars': xxx, # 等于optPop.Phen，此处即最优解。若无可行解，则Vars=None。
'ObjV': xxx, # 等于optPop.ObjV，此处即最优解对应的目标函数值。若无可行解，ObjV=None。
'CV': xxx, # 等于optPop.CV，此处即最优解对应的违反约束程度矩阵。若无可行解，CV=None。
'startTime': xxx, # 程序执行开始时间。
'endTime': xxx, # 程序执行结束时间。
'executeTime': xxx, # 算法所用时间。
'nfev': xxx, # 算法评价次数
'gd': xxx, # (多目标优化且给定了理论最优解时才有) GD指标值。
'igd': xxx, # (多目标优化且给定了理论最优解时才有) IGD指标值。
'hv': xxx, # (多目标优化才有) HV指标值。
'spacing': xxx} # (多目标优化才有) Spacing指标值。
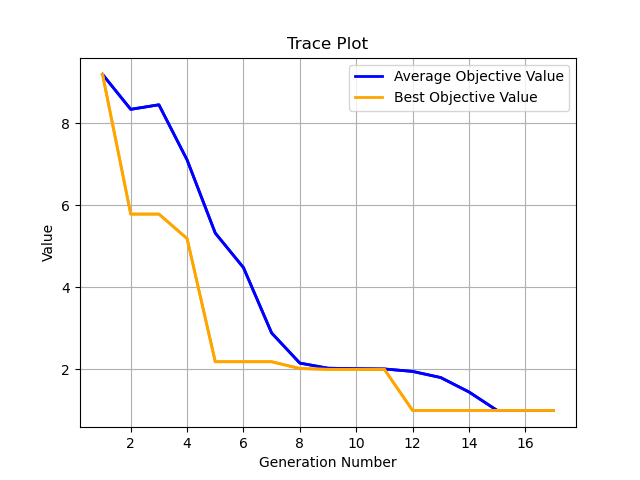
结果
====================================================================
gen| eval | f_opt | f_max | f_avg | f_min | f_std
----------------------------------------------------------------------------------
0 | 20 | 9.18566E+00 | 9.18566E+00 | 9.18566E+00 | 9.18566E+00 | 0.00000E+00
1 | 40 | 5.78235E+00 | 9.18566E+00 | 8.33483E+00 | 5.78235E+00 | 1.47368E+00
2 | 60 | 5.78235E+00 | 1.01857E+01 | 8.44530E+00 | 5.78235E+00 | 1.56014E+00
3 | 80 | 5.18566E+00 | 9.18566E+00 | 7.10178E+00 | 5.18566E+00 | 1.70646E+00
4 | 100 | 2.18566E+00 | 5.78235E+00 | 5.31974E+00 | 2.18566E+00 | 1.00074E+00
5 | 120 | 2.18566E+00 | 5.71252E+00 | 4.47875E+00 | 2.18566E+00 | 1.38039E+00
6 | 140 | 2.18566E+00 | 5.18566E+00 | 2.88560E+00 | 2.18566E+00 | 1.09847E+00
7 | 160 | 2.02037E+00 | 2.18566E+00 | 2.15260E+00 | 2.02037E+00 | 6.61145E-02
8 | 180 | 2.00000E+00 | 2.18565E+00 | 2.02762E+00 | 2.00000E+00 | 3.65244E-02
9 | 200 | 2.00000E+00 | 2.02037E+00 | 2.01625E+00 | 2.00000E+00 | 8.12936E-03
10| 220 | 2.00000E+00 | 2.02037E+00 | 2.00908E+00 | 2.00000E+00 | 9.96122E-03
11| 240 | 1.00000E+00 | 2.00000E+00 | 1.95000E+00 | 1.00000E+00 | 2.17945E-01
12| 260 | 1.00000E+00 | 2.00000E+00 | 1.80000E+00 | 1.00000E+00 | 4.00000E-01
13| 280 | 1.00000E+00 | 2.00000E+00 | 1.45000E+00 | 1.00000E+00 | 4.97494E-01
14| 300 | 1.00000E+00 | 1.00000E+00 | 1.00000E+00 | 1.00000E+00 | 0.00000E+00
15| 320 | 1.00000E+00 | 1.00000E+00 | 1.00000E+00 | 1.00000E+00 | 0.00000E+00
16| 340 | 1.00000E+00 | 1.00000E+00 | 1.00000E+00 | 1.00000E+00 | 0.00000E+00
Execution time: 0.012000560760498047 s
Evaluation number: 340
The best objective value is: 1.0
The best variables are:
1.0 1.0 2.0 1.0 1.0
案例 2
同样是求解案例1的问题，这里我们在定义目标函数时不加ea.Problem.single标记。这意味着evalVars()传入的是一个Numpy ndarray二维数组。下面直接看代码：
# 构建问题
r = 1 # 模拟该案例问题计算目标函数时需要用到的额外数据
def evalVars(Vars): # 定义目标函数（含约束）
ObjV = np.sum((Vars - r) ** 2, 1, keepdims=True) # 计算目标函数值
x1 = Vars[:, [0]] # 把Vars的第0列取出来
x2 = Vars[:, [1]] # 把Vars的第1列取出来
CV = np.hstack([(x1 - 0.5) ** 2 - 0.25,
(x2 - 1) ** 2 - 1]) # 计算违反约束程度
return ObjV, CV # 返回目标函数值矩阵和违反约束程度矩阵
problem = ea.Problem(name='soea quick start demo',
M=1, # 目标维数
maxormins=[1], # 目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标
Dim=5, # 决策变量维数
varTypes=[0, 0, 1, 1, 1], # 决策变量的类型列表，0：实数；1：整数
lb=[-1, 1, 2, 1, 0], # 决策变量下界
ub=[1, 4, 5, 2, 1], # 决策变量上界
evalVars=evalVars)
# 构建算法
algorithm = ea.soea_SEGA_templet(problem,
ea.Population(Encoding='RI', NIND=20),
MAXGEN=50, # 最大进化代数。
logTras=1, # 表示每隔多少代记录一次日志信息，0表示不记录。
trappedValue=1e-6, # 单目标优化陷入停滞的判断阈值。
maxTrappedCount=10) # 进化停滞计数器最大上限值。
# 求解
res = ea.optimize(algorithm, seed=1, verbose=True, drawing=1, outputMsg=True, drawLog=False, saveFlag=True, dirName='result')
可以发现，发生最大变化的是目标函数的定义上。不加ea.Problem.single标记后，传入目标函数evalVars()的参数Vars是一个Numpy ndarray二维数组。它是NIND行Dim列。NIND即种群的个体数，即种群规模；Dim即自定义的问题的决策变量个数。
因此我们可以用Numpy向量化的方法同时算出所有个体对应的目标函数值和违反约束程度值。结果分别保存为ObjV和CV。其中ObjV是一个NIND行1列的Numpy ndarray二维数组。CV是一个NIND行2列的Numpy ndarray二维数组。
2、面向对象模式入门
案例 3
用NSGA2算法求解下面的双目标优化问题：
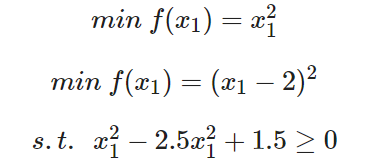
“面向对象”风格的写法：
class MyProblem(ea.Problem): # 继承Problem父类
def __init__(self):
name = 'MyProblem' # 初始化name（函数名称，可以随意设置）
M = 2 # 优化目标个数
maxormins = [1] * M # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
Dim = 1 # 初始化Dim（决策变量维数）
varTypes = [0] # 初始化varTypes（决策变量的类型，0：实数；1：整数）
lb = [-10] # 决策变量下界
ub = [10] # 决策变量上界
lbin = [1] # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
ubin = [1] # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
# 调用父类构造方法完成实例化
ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
def evalVars(self, Vars): # 目标函数
f1 = Vars ** 2
f2 = (Vars - 2) ** 2
ObjV = np.hstack([f1, f2]) # 计算目标函数值矩阵
CV = -Vars ** 2 + 2.5 * Vars - 1.5 # 构建违反约束程度矩阵
return ObjV, CV
# 实例化问题对象
problem = MyProblem()
# 构建算法
algorithm = ea.moea_NSGA2_templet(problem,
ea.Population(Encoding='RI', NIND=50),
MAXGEN=200, # 最大进化代数
logTras=0) # 表示每隔多少代记录一次日志信息，0表示不记录。
# 求解
res = ea.optimize(algorithm, seed=1, verbose=False, drawing=1, outputMsg=True, drawLog=False, saveFlag=False, dirName='result')
这里通过构建geatpy问题类Problem的子类来定义问题。第14行定义了目标函数evalVars，它重写了Problem类中的evalVars()。注意这个名字不能随便更改。Geatpy的Problem问题类提供两种目标函数的定义，分别是evalVars和aimFunc。前者（evalVars）是Geatpy2.7.0之后新增的写法，它传入决策变量矩阵Vars且需要返回对应的目标函数值矩阵ObjV和违反约束程度矩阵CV（若待求解的问题没有约束条件，则可以只返回目标函数矩阵）。后者（aimFunc）是传统的写法，它传入一个种群对象，且不需要返回值。
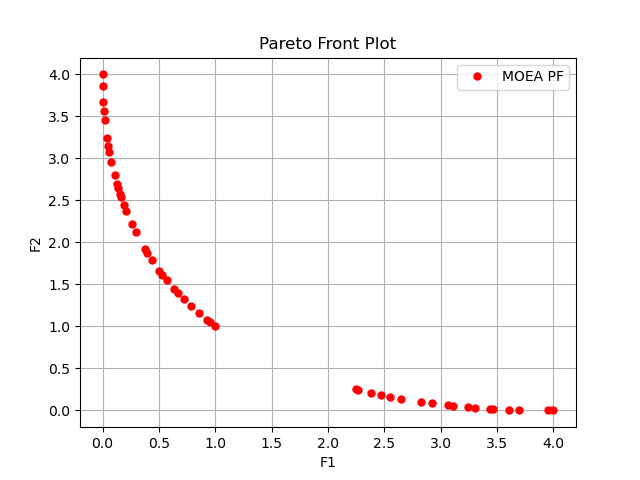
Execution time: 0.0790555477142334 s
Evaluation number: 10000
The number of non-dominated solutions is: 50
hv: 0.83020
spacing: 0.03503
二、 Geatpy架构说明
Geatpy2整体上看由工具箱内核函数（内核层）和面向对象进化算法框架（框架层）两部分组成。其中面向对象进化算法框架主要有四个大类：Problem问题类、Algorithm算法模板类、Population种群类和PsyPopulation多染色体种群类。UML图如下所示：
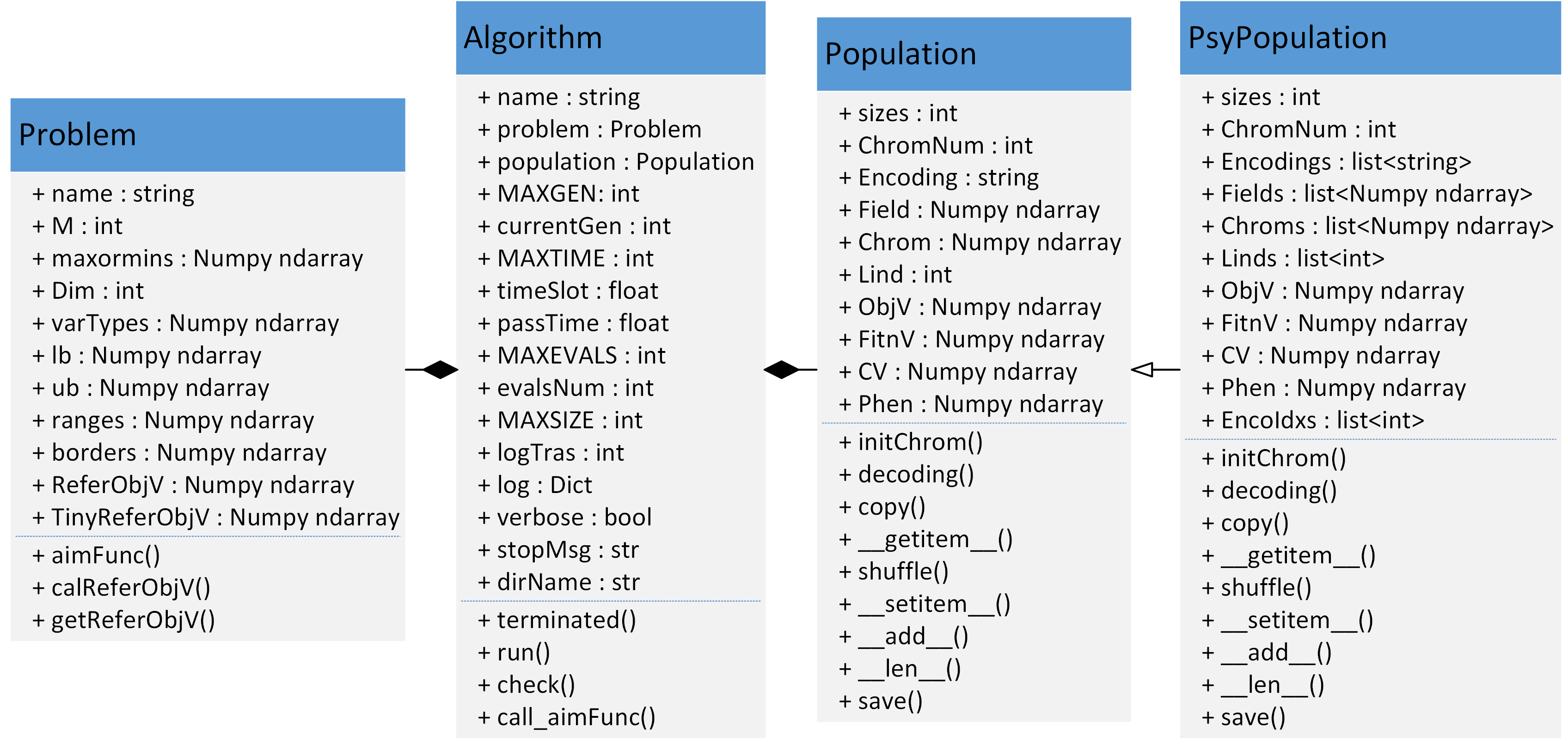
Problem类定义了与问题相关的一些信息，如问题名称name、优化目标的维数M、决策变量的个数Dim、决策变量的范围ranges、决策变量的边界borders等。maxormins是一个记录着各个目标函数是最小化抑或是最大化的Numpy array行向量，其中元素为1表示对应的目标是最小化目标；为-1表示对应的是最大化目标。例如M=3，maxormins=array([1,-1,1])，此时表示有三个优化目标，其中第一、第三个是最小化目标，第二个是最大化目标。varTypes是一个记录着决策变量类型的行向量，其中的元素为0表示对应的决策变量是连续型变量；为1表示对应的是离散型变量。待求解的目标函数定义在aimFunc()的函数中。calReferObjV()函数则用于计算或读取目标函数参考值（一般用理论上的目标函数的最优值作为参考值），该参考值可以用于后续的指标分析。在实际使用时，不是直接在Problem类的文件中修改相关代码来使用的，而是通过定义一个继承Problem的子类来完成对问题的定义的。这些在后面的章节中会详细讲述。getReferObjV()是Problem父类中已经实现了的一个函数，它先尝试读取特定文件夹中的目标函数值参考数据，如果读取不到，则调用calReferObjV()进行计算。对于Problem类中各属性的详细含义可查看Problem.py源码。
Population 类是一个表示种群的类。一个种群包含很多个个体，而每个个体都有一条染色体(若要用多染色体，则使用多个种群、并把每个种群对应个体关联起来即可)。除了染色体外，每个个体都有一个译码矩阵Field(或俗称区域描述器) 来标识染色体应该如何解码得到表现型，同时也有其对应的目标函数值以及适应度。种群类就是一个把所有个体的这些数据统一存储起来的一个类。比如里面的Chrom 是一个存储种群所有个体染色体的矩阵，它的每一行对应一个个体的染色体；ObjV 是一个目标函数值矩阵，每一行对应一个个体的所有目标函数值，每一列对应一个目标。对于Population 类中各属性的详细含义可查看Population.py 源码以及下一章“Geatpy 数据结构”。
PsyPopulation类是继承了Population的支持多染色体混合编码的种群类。一个种群包含很多个个体，而每个个体都有多条染色体。用Chroms列表存储所有的染色体矩阵(Chrom)；Encodings列表存储各染色体对应的编码方式(Encoding)；Fields列表存储各染色体对应的译码矩阵(Field)。EncoIdxs是一个list，其元素表示每条染色体对应编码哪一个变量。比如EncoIdxs = [[0], [1,2,3,4]]，表示一共有5个变量，其中第一个变量编码成第一条子染色体；后4个变量编码成第二条子染色体。
Algorithm 类是进化算法的核心类。它既存储着跟进化算法相关的一些参数，同时也在其继承类中实现具体的进化算法。比如Geatpy 中的moea_NSGA3_templet.py 是实现了多目标优化NSGA-III 算法的进化算法模板类，它是继承了Algorithm 类的具体算法的模板类。关于Algorithm 类中各属性的含义可以查看Algorithm.py 源码。这些算法模板通过调用Geatpy 工具箱提供的进化算法库函数实现对种群的进化操作，同时记录进化过程中的相关信息，其基本层次结构如下图：
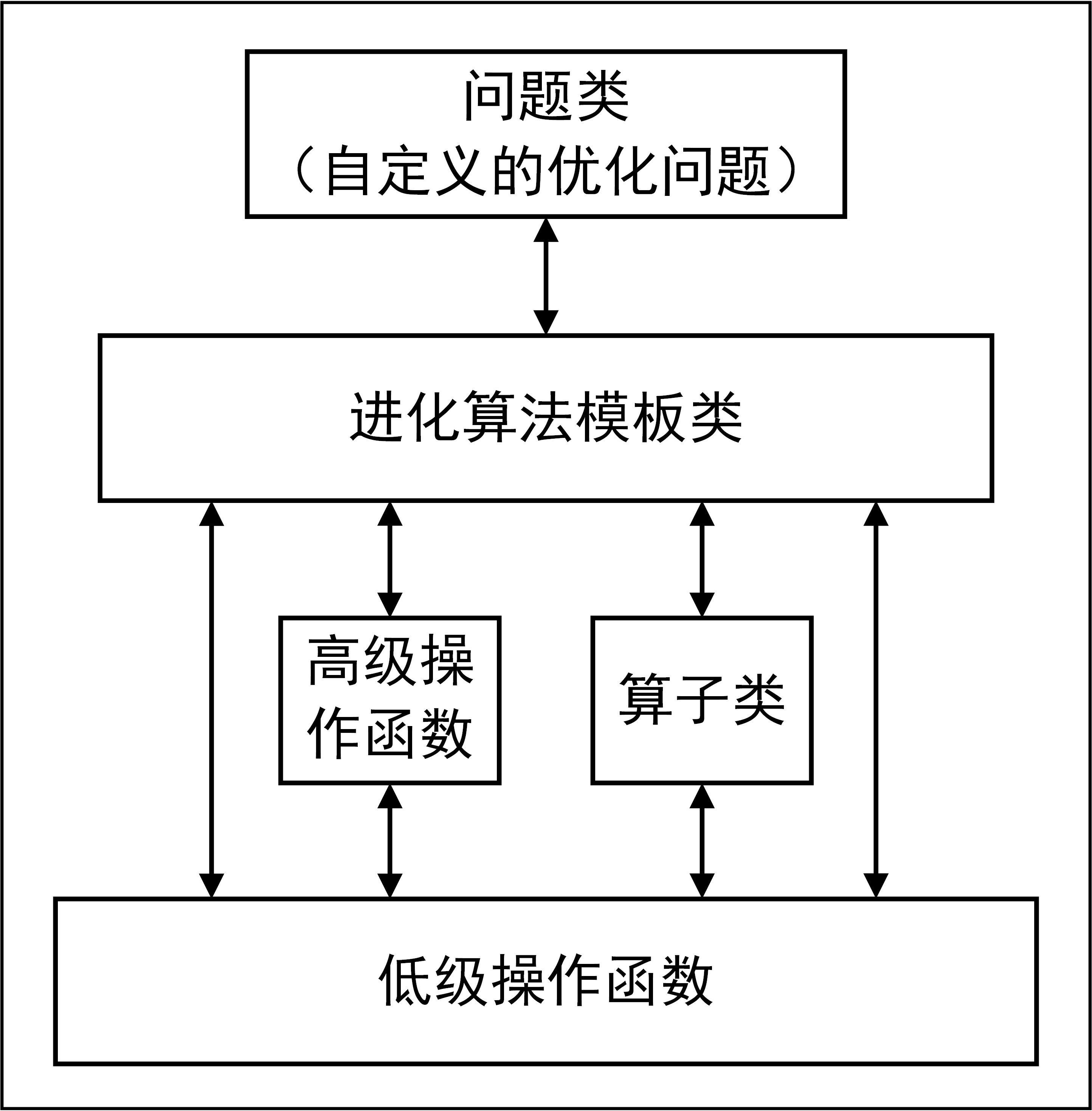
其中“算子类”是Geatpy2.2.2版本之后增加的特性，通过实例化算子类来调用低级操作函数，可以利用面向对象编程的优势使得对传入低级操作函数的一些参数的修改变得更加方便。目前内置的“算子类”有“重组算子类”和“变异算子类”。用户可以绕开对底层的低级操作函数的修改而直接通过新增“算子类”来实现新的算子例如自适应的重组、变异算子等。
例如：mutpolyn是多项式变异的低级变异算子。其对应的高级变异算子为：Mutpolyn。
