图->遍历
文字描述
从图中某一顶点出发遍历图中其余顶点,且使每一个顶点仅被访问一次,这一过程就叫图的遍历。
深度优先搜索:类似树的先根遍历;假设初始状态下,图中所有顶点都未曾被访问,则从某个顶点出发,访问此顶点,然后依次从v的未被访问的邻接点出发继续深度优先遍历图,直到图中所有和v有路径相通的顶点都被访问到;若此时图中尚有顶点未被访问,则另选一个未曾被访问的顶点作起始点。
广度优先搜索:类似数的层次遍历;以v为起始点,由近及远,依次访问和v有路径相通且路径长度为1,2,…的顶点。
示意图

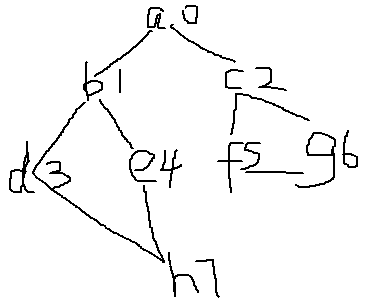
算法分析
深度优先搜索:遍历图的过程实质上是对每个顶点找其邻接点的过程。其耗费的时间取决于所采用的存储结构。当用二维数组表示邻接矩阵作图的存储结构时,查找每个顶点的邻接点所需时间为n*n, 其中n为图中顶点数。而当以邻接表作图的存储结构时,找邻接点所需时间为e,其中e为无向图中的边数或有向图中弧的数。由此,当以邻接表作存储结构时,深度优先搜索遍历图的时间复杂度为n+e。
广度优先搜索:其时间复杂度和深度优先遍历相同,两者不同之处在于对顶点的访问顺序不同。
代码实现

1 /* 2 1.以邻接表作为图的存储结构创建图。 3 2.用深度优先搜索的方法对图中结点进行遍历 4 3.用广度优先搜索的方法对图中结点进行遍历 5 */ 6 7 #include <stdio.h> 8 #include <stdlib.h> 9 #include <string.h> 10 11 #define INFINITY 100000 //最大值 12 #define MAX_VERTEX_NUM 20 //最大顶点数 13 #define None -1 14 typedef enum {DG, DN, UDG, UDN} GraphKind; //{有向图,有向网,无向图,无向网} 15 typedef char VertexType; 16 typedef struct{ 17 char note[10]; 18 }InfoType; 19 //与顶点相连的弧结点 20 typedef struct ArcNode{ 21 int adjvex; //该弧所指向的顶点的位置 22 struct ArcNode *nextarc; //指向下一条弧的指针 23 InfoType *info; //该弧相关信息的指针 24 }ArcNode; 25 //顶点结点 26 typedef struct VNode{ 27 VertexType data;//顶点信息 28 ArcNode *firstarc;//指向第一条依附该顶点的弧的指针 29 }VNode, AdjList[MAX_VERTEX_NUM]; 30 //图结点 31 typedef struct{ 32 AdjList vertices; 33 int vexnum;//图的顶点数 34 int arcnum;//图的弧数 35 int kind; //图的种类标志 36 }ALGraph; 37 38 /* 39 若G中存在顶点u,则返回该顶点在图中位置;否则返回-1。 40 */ 41 int LocateVex(ALGraph G, VertexType v) 42 { 43 int i = 0; 44 for(i=0; i<G.vexnum; i++){ 45 if(G.vertices[i].data == v){ 46 return i; 47 } 48 } 49 return -1; 50 } 51 52 /* 53 在链表L的头部前插入v 54 */ 55 int InsFirst(ArcNode *L, int v) 56 { 57 ArcNode *n = (ArcNode *)malloc(sizeof(struct ArcNode)); 58 n->adjvex = v; 59 n->nextarc = L->nextarc; 60 L->nextarc = n; 61 return 0; 62 } 63 64 /* 65 采用邻接表的存储结构,构造无向图 66 */ 67 int CreateUDG(ALGraph *G) 68 { 69 int i = 0, j = 0, k = 0, IncInfo = 0; 70 int v1 = 0, v2 = 0; 71 char tmp[10] = {0}; 72 73 printf("输入顶点数,弧数,其他信息标志位: "); 74 scanf("%d,%d,%d", &G->vexnum, &G->arcnum, &IncInfo); 75 76 for(i=0; i<G->vexnum; i++){ 77 printf("输入第%d个顶点: ", i+1); 78 memset(tmp, 0, sizeof(tmp)); 79 scanf("%s", tmp); 80 G->vertices[i].data = tmp[0]; 81 G->vertices[i].firstarc = malloc(sizeof(struct ArcNode)); 82 G->vertices[i].firstarc->adjvex = None; 83 G->vertices[i].firstarc->nextarc = NULL; 84 } 85 86 for(k=0; k<G->arcnum; k++){ 87 printf("输入第%d条弧(顶点1, 顶点2): ", k+1); 88 memset(tmp, 0, sizeof(tmp)); 89 scanf("%s", tmp); 90 sscanf(tmp, "%c,%c", &v1, &v2); 91 i = LocateVex(*G, v1); 92 j = LocateVex(*G, v2); 93 InsFirst(G->vertices[i].firstarc, j); 94 InsFirst(G->vertices[j].firstarc, i); 95 if(IncInfo){ 96 //other info on arc 97 } 98 } 99 return 0; 100 } 101 102 /* 103 采用邻接表的存储结构,构造图 104 */ 105 int CreateGraph(ALGraph *G) 106 { 107 printf("输入图类型: -有向图(0), -有向网(1), +无向图(2), -无向网(3): "); 108 scanf("%d", &G->kind); 109 switch(G->kind){ 110 case DG: 111 case DN: 112 case UDN: 113 printf("还不支持!\n"); 114 return -1; 115 case UDG: 116 return CreateUDG(G); 117 default: 118 return -1; 119 } 120 } 121 122 /* 123 输出图的信息 124 */ 125 void printG(ALGraph G) 126 { 127 if(G.kind == DG){ 128 printf("类型:有向图;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum); 129 }else if(G.kind == DN){ 130 printf("类型:有向网;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum); 131 }else if(G.kind == UDG){ 132 printf("类型:无向图;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum); 133 }else if(G.kind == UDN){ 134 printf("类型:无向网;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum); 135 } 136 int i = 0; 137 ArcNode *p = NULL; 138 for(i=0; i<G.vexnum; i++){ 139 printf("%c\t", G.vertices[i].data); 140 p = G.vertices[i].firstarc; 141 while(p){ 142 if(p->adjvex != None) 143 printf("%d\t", p->adjvex); 144 p = p->nextarc; 145 } 146 printf("\n"); 147 } 148 return; 149 } 150 151 152 ////////////////////////////////////////////////////////////////////// 153 ////////////////////////////////////////////////////////////////////// 154 ////////////////////////////////////////////////////////////////////// 155 ////////////////////////////////////////////////////////////////////// 156 //开始用深度优先搜索的方法对图中结点进行遍历 157 int Visited[MAX_VERTEX_NUM] = {0};//访问标志数组 158 void (*VisitFun)(ALGraph G, int v);//函数变量 159 160 //打印顶点中位置v的顶点信息 161 void printfun(ALGraph G, int v){ 162 printf("[%d]:%c\t", v, G.vertices[v].data); 163 } 164 165 //返回图G中与顶点位置为v的顶点相连的第一个结点在顶点中的位置 166 int FirstAdjVex(ALGraph G, int v) 167 { 168 return G.vertices[v].firstarc->nextarc->adjvex; 169 } 170 171 //返回图G中与顶点位置为v的顶点相连的结点w的下一个结点在顶点中的位置 172 int NextAdjVex(ALGraph G, int v, int w) 173 { 174 ArcNode *arc = G.vertices[v].firstarc; 175 while(arc && arc->adjvex != w){ 176 arc = arc->nextarc; 177 } 178 if(arc && arc->nextarc){ 179 return arc->nextarc->adjvex; 180 } 181 return -1; 182 } 183 184 //从第v个顶点出发递归地深度优先遍历图G 185 void DFS(ALGraph G, int v){ 186 //访问第v个顶点 187 Visited[v] = 1; 188 VisitFun(G, v); 189 int w = 0; 190 for(w=FirstAdjVex(G,v); w>=0; w=NextAdjVex(G,v,w)){ 191 //对v的尚未访问的邻接顶点w递归调用DFS 192 if(!Visited[w]){ 193 DFS(G,w); 194 } 195 } 196 } 197 198 //对图G作深度优先遍历 199 void DFSTraverse(ALGraph G, void (*Visit)(ALGraph G, int v)) 200 { 201 printf("深度优先搜索: "); 202 //使用全局变量VisitFun, 是DFS不必设函数指针参数 203 VisitFun = Visit; 204 int v = 0; 205 //访问标志数组初始化 206 for(v=0; v<G.vexnum; v++){ 207 Visited[v] = 0; 208 } 209 for(v=0; v<G.vexnum; v++){ 210 //对尚未访问的顶点调用DFS 211 if(!Visited[v]) 212 DFS(G, v); 213 } 214 } 215 216 217 ////////////////////////////////////////////////////////////////////// 218 ////////////////////////////////////////////////////////////////////// 219 ////////////////////////////////////////////////////////////////////// 220 ////////////////////////////////////////////////////////////////////// 221 //开始用广度优先搜索的方法对图中结点进行遍历 222 typedef struct QNode{ 223 int data; 224 struct QNode *next; 225 }QNode, *QuenePtr; 226 227 typedef struct{ 228 QuenePtr front; 229 QuenePtr rear; 230 }LinkQueue; 231 LinkQueue *InitQueue(void){ 232 LinkQueue *Q = (LinkQueue*)malloc(sizeof(LinkQueue)); 233 Q->front = Q->rear = (QuenePtr)malloc(sizeof(QNode)); 234 Q->front->next = Q->rear->next = NULL; 235 return Q; 236 } 237 int QueueEmpty(LinkQueue *Q){ 238 if(Q->front == Q->rear){ 239 return 0; 240 }else{ 241 return -1; 242 } 243 } 244 int EnQueue(LinkQueue *Q, int e){ 245 QuenePtr p = (QuenePtr)malloc(sizeof(QNode)); 246 p->data = e; 247 p->next = NULL; 248 Q->rear->next = p; 249 Q->rear = p; 250 return 0; 251 } 252 253 int DeQueue(LinkQueue *Q, int *e) 254 { 255 if(Q->rear == Q->front){ 256 return -1; 257 } 258 QuenePtr p = Q->front->next; 259 *e = p->data; 260 Q->front->next = p->next; 261 if(p == Q->rear){ 262 Q->rear = Q->front; 263 } 264 free(p); 265 return 0; 266 } 267 268 void PrintQ(LinkQueue *Q) 269 { 270 QuenePtr head = Q->front; 271 while(head){ 272 printf("%d\t", head->data); 273 head = head->next; 274 } 275 printf("\n"); 276 } 277 278 /*广度优先搜索 279 *按广度优先非递归遍历图G。使用辅助队列Q和访问标志数组Visited 280 */ 281 void BFSTraverse(ALGraph G, void (*Visit)(ALGraph G, int v)) 282 { 283 printf("广度优先搜索: "); 284 int v = 0; 285 int u = 0; 286 int w = 0; 287 //访问标志数组初始化 288 for(v=0; v<G.vexnum; v++){ 289 Visited[v] = 0; 290 } 291 //置空的辅助队列Q 292 LinkQueue *Q = InitQueue(); 293 for(v=0; v<G.vexnum; v++){ 294 if(!Visited[v]){ 295 //v尚未访问 296 Visited[v] = 1; 297 //访问v顶点 298 Visit(G, v); 299 //v入队列 300 EnQueue(Q, v); 301 302 while(QueueEmpty(Q)){ 303 //队头元素出队并置为u 304 DeQueue(Q, &u); 305 for(w=FirstAdjVex(G, u); w>=0; w=NextAdjVex(G, u, w)){ 306 if(!Visited[w]){ 307 //w为u的尚未访问的邻接顶点 308 Visited[w] = 1; 309 Visit(G, w); 310 EnQueue(Q, w); 311 } 312 } 313 } 314 } 315 } 316 } 317 318 int main(int argc, char *argv[]) 319 { 320 ALGraph G; 321 if(CreateGraph(&G) > -1){ 322 printG(G); 323 } 324 DFSTraverse(G, printfun);printf("\n"); 325 BFSTraverse(G, printfun);printf("\n"); 326 return 0; 327 }
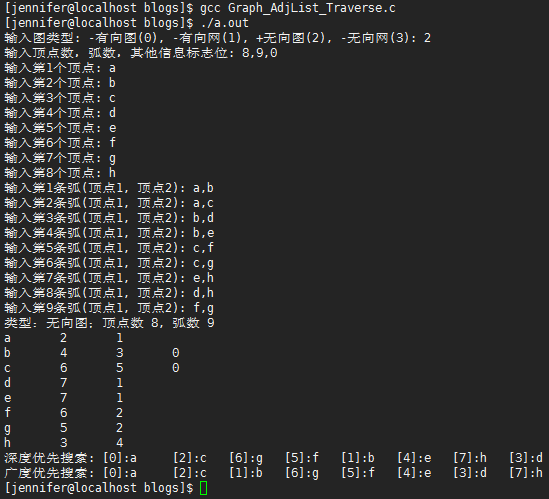
代码运行
posted on 2018-10-10 18:14 LiveWithACat 阅读(649) 评论(0) 收藏 举报


 浙公网安备 33010602011771号
浙公网安备 33010602011771号