图->存储结构->邻接表
文字描述
邻接表是图的一种链式存储结构。在邻接表中,对图中每个顶点建立一个单链表,第i个单链表的结点表示依附顶点vi的边(对有向图是指以顶点vi为尾的弧)。单链表中的每个结点由3个域组成,其中邻接点域adjvex指示与顶点vi邻接的点在图中的位置;链域nextarc指示下一条边或弧的结点;数据域info存储和边或弧相关的信息如权值等。每个链表上附设一个表头结点,在表头结点中,除了设有链域firstarc指向链表中第一个结点外,还设有存储顶点vi的名或其他有关信息的数据域data。
在无向图的邻接表中,顶点vi的度恰为第i个单链表中的结点数;而在有向图中,第i个链表中的结点数只是顶点vi的出度,为求入度,需便历整个邻接表;为了方便确定顶点的入度或以顶点vi为头的弧,可以建立一个有向图的逆邻接表,即对每个顶点vi建立一个了链接以vi为头的弧的表。

示意图
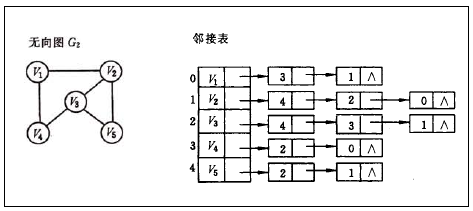

算法分析
在建立邻接表或逆邻接表时,若输入的顶点信息就是顶点的编号,则建立邻接表的时间复杂度为n+e;否则,需要通过查找才能得到顶点在图中位置,则时间复杂度为n*e.
在邻接表上容易找到任一顶点的第一个邻接点和下一个领接点,但要判定任意两个顶点(vi和vj)之间是否有边或弧相连,则需搜索第i个或第j个链表;因此,不及邻接矩阵方便。
代码实现

1 /* 2 以邻接表作为图的存储结构创建图。 3 */ 4 5 #include <stdio.h> 6 #include <stdlib.h> 7 #include <string.h> 8 9 #define INFINITY 100000 //最大值 10 #define MAX_VERTEX_NUM 20 //最大顶点数 11 #define None -1 12 typedef enum {DG, DN, UDG, UDN} GraphKind; //{有向图,有向网,无向图,无向网} 13 typedef char VertexType; 14 typedef struct{ 15 char note[10]; 16 }InfoType; 17 //表结点 18 typedef struct ArcNode{ 19 int adjvex; //该弧所指向的顶点的位置 20 struct ArcNode *nextarc; //指向下一条弧的指针 21 InfoType *info; //该弧相关信息的指针 22 }ArcNode; 23 //头结点 24 typedef struct VNode{ 25 VertexType data;//顶点信息 26 ArcNode *firstarc;//指向第一条依附该顶点的弧的指针 27 }VNode, AdjList[MAX_VERTEX_NUM]; 28 typedef struct{ 29 AdjList vertices; 30 int vexnum;//图的顶点数 31 int arcnum;//图的弧数 32 int kind; //图的种类标志 33 }ALGraph; 34 35 /* 36 若G中存在顶点u,则返回该顶点在图中位置;否则返回-1。 37 */ 38 int LocateVex(ALGraph G, VertexType v) 39 { 40 int i = 0; 41 for(i=0; i<G.vexnum; i++){ 42 if(G.vertices[i].data == v){ 43 return i; 44 } 45 } 46 return -1; 47 } 48 49 /* 50 在链表L的头部前插入v 51 */ 52 int InsFirst(ArcNode *L, int v) 53 { 54 ArcNode *n = (ArcNode *)malloc(sizeof(struct ArcNode)); 55 n->adjvex = v; 56 n->nextarc = L->nextarc; 57 L->nextarc = n; 58 return 0; 59 } 60 61 /* 62 采用邻接表的存储结构,构造无向图 63 */ 64 int CreateUDG(ALGraph *G) 65 { 66 int i = 0, j = 0, k = 0, IncInfo = 0; 67 int v1 = 0, v2 = 0; 68 char tmp[10] = {0}; 69 70 printf("输入顶点数,弧数,其他信息标志位: "); 71 scanf("%d,%d,%d", &G->vexnum, &G->arcnum, &IncInfo); 72 73 for(i=0; i<G->vexnum; i++){ 74 printf("输入第%d个顶点: ", i+1); 75 memset(tmp, 0, sizeof(tmp)); 76 scanf("%s", tmp); 77 G->vertices[i].data = tmp[0]; 78 G->vertices[i].firstarc = malloc(sizeof(struct ArcNode)); 79 G->vertices[i].firstarc->adjvex = None; 80 G->vertices[i].firstarc->nextarc = NULL; 81 } 82 83 for(k=0; k<G->arcnum; k++){ 84 printf("输入第%d条弧(顶点1, 顶点2): ", k+1); 85 memset(tmp, 0, sizeof(tmp)); 86 scanf("%s", tmp); 87 sscanf(tmp, "%c,%c", &v1, &v2); 88 i = LocateVex(*G, v1); 89 j = LocateVex(*G, v2); 90 InsFirst(G->vertices[i].firstarc, j); 91 InsFirst(G->vertices[j].firstarc, i); 92 if(IncInfo){ 93 //other info on arc 94 } 95 } 96 return 0; 97 } 98 99 /* 100 采用邻接表的存储结构,构造图 101 */ 102 int CreateGraph(ALGraph *G) 103 { 104 printf("输入图类型: -有向图(0), -有向网(1), +无向图(2), -无向网(3): "); 105 scanf("%d", &G->kind); 106 switch(G->kind){ 107 case DG: 108 case DN: 109 case UDN: 110 printf("还不支持!\n"); 111 return -1; 112 case UDG: 113 return CreateUDG(G); 114 default: 115 return -1; 116 } 117 } 118 119 /* 120 输出图的信息 121 */ 122 void printG(ALGraph G) 123 { 124 if(G.kind == DG){ 125 printf("类型:有向图;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum); 126 }else if(G.kind == DN){ 127 printf("类型:有向网;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum); 128 }else if(G.kind == UDG){ 129 printf("类型:无向图;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum); 130 }else if(G.kind == UDN){ 131 printf("类型:无向网;顶点数 %d, 弧数 %d\n", G.vexnum, G.arcnum); 132 } 133 int i = 0; 134 ArcNode *p = NULL; 135 for(i=0; i<G.vexnum; i++){ 136 printf("%c\t", G.vertices[i].data); 137 p = G.vertices[i].firstarc; 138 while(p){ 139 if(p->adjvex != None) 140 printf("%d\t", p->adjvex); 141 p = p->nextarc; 142 } 143 printf("\n"); 144 } 145 return; 146 } 147 148 int main(int argc, char *argv[]) 149 { 150 ALGraph G; 151 if(CreateGraph(&G) > -1){ 152 printG(G); 153 } 154 return 0; 155 }
代码运行

posted on 2018-10-02 18:15 LiveWithACat 阅读(1363) 评论(0) 收藏 举报


 浙公网安备 33010602011771号
浙公网安备 33010602011771号