查找->动态查找表->B-树(无代码)

 文字描述

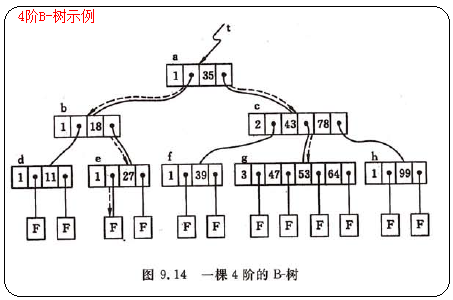
B-树定义

　　一颗m阶的B-树,或者是空树,或者是满足下列特性的m叉树:

　　(1) 树中每个结点至多m颗子树

　　(2) 若根结点不是叶子结点,则根结点至少有两颗子树

　　(3) 除根结点外的所有非终端结点至少有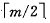棵子树

　　(4) 所有非终端结点中包含下列信息数据(n, A0, K₁, A₁, K₂, A₂,…,K_n,A_n)

　　其中K_i(i=1,…,n)为关键字，且K_i < K_i+1(i=1,…,n-1)；A_i(i=0,…,n)为指向子树根结点的指针，且A_i-1所指子树中所有结点的关键字均小于K_i(i=1,…,n)，A_n所指子树中所有结点的关键字均大于K_n，n([m/2]-1 <= n <= m-1)为关键字的个数(或n+1个子树个数)。

　　(5) 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点，实际上这些结点不存在，指向这些结点的指针为空)。

 

B-树查找算法

　　查找分两步：

　　(1)   在B-树找到结点

　　(2)   在结点上找到关键字

　　B-树主要用作文件的索引且B-树通常存储在磁盘上，则第(1)步是在磁盘上进行的，而第(2)步是在内存上进行的。即在磁盘上找到结点后，先将结点中信息读入内存，然后，再利用顺序查找或二分查找查询等于K的关键码。由此可见，在B-树上进行查找的过程是一个顺序查找结点和在结点的关键字中进行查找交叉进行的过程。

 

B-树插入算法   

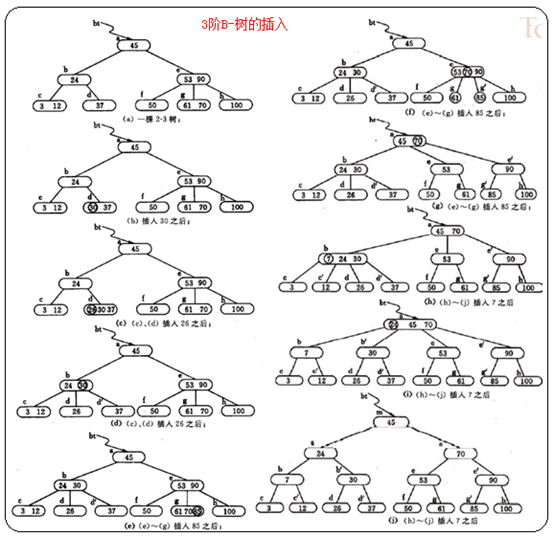
　　B-树的生成也是从空树起，逐个插入关键字而得。但由于B-树结点中的关键字个数必须大于等于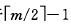，因此，每插入一个关键字不是在树中添加一个叶子结点，而是首先在最底层的某个非终端结点中添加一个关键字，若该结点中的关键字个数不超过m-1，则插入完成，否则要产生结点的“分裂”。一般情况下，结点可按照如下实现“分裂”:

　　假设*p结点中已有m-1个关键字，当插入一个关键字后，

　　结点中含有信息为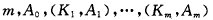： , K_i < K_i+1 (1<= i <m), 此时可将*p结点分裂成为*p和*p‘两个结点，其中

　　*p为：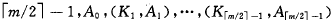

　　*p’结点中含有信息为：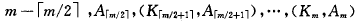

　　而关键字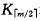和指针*p’一起插入到*p的双亲结点中。

 

B-树删除算法

　　首先应找到该关键字所在结点，并从中删除之。若该结点为最下层的非终端结点，且其中的关键字树目不少于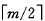，则删除完成，否则要进行“合并”。假若所删关键字为非终端结点中的K_i, 则可以将指针A_i所指子树中的最小关键字Y替代K_i，然后在相应的结点中删去Y。因此，只需讨论删除最下层非终端结点中的关键字的情形:

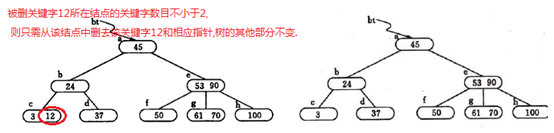
　　(1)   被删关键字所在结点中的关键字数目不小于，则只需从该结点中删去该关键字Ki和相应指针Ai，树的其他部分不变。

 

 　　(2)被删关键字所在结点中的关键字数目等于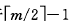,,而与该结点相邻的兄弟结点中的关键字树目大于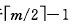,则需将其兄弟结点中的最值(左兄弟就是最大值，右兄弟就是最小值)的关键字上移至双亲结点中，而将双亲结点中小于(或大于)且紧靠上移关键字的关键字下移至被删关键字所在结点中。

 

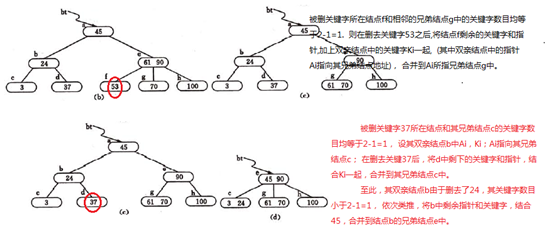
　　(3)被删关键字所在结点和其相邻的兄弟的关键字数目均等于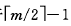。假设该结点有右兄弟，且其右兄弟结点地址由双亲结点中的指针A_i所指，则在删去关键字之后，它所在结点中剩余的关键字和指针，加上双亲结点中的关键字K_i一起，合并到A_i所指兄弟结点中。如果因此使双亲结点中的关键字数目小于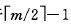，则依次类推作相应处理。

 

 

 示意图

 

 

 

算法分析(B-树查找算法分析)

　　在B-树上查找一个关键字，分两步(1)在B-树中找结点；(2)在结点中找关键字；前一步查找是在磁盘上进行的，后一步查找是在内存上进行的。显然，在磁盘上进行一次查找比在内存中进行一次查找耗费时间更多，因此，在磁盘上进行查找的次数、即待查关键字所在结点在B-树上的层次数，是决定B-树查找效率的首要因素。那么最坏情况下，含N个关键字的m阶B-树的最大深度是多少？

 　　先讨论深度为l+1的m阶B-树所具有的最少结点数。按B-树的定义，第一层至少有1个结点；第二层至少有2个结点；由于除根之外的每个非终端结点至少有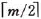棵子树，则第三层至少有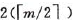个结点；,,,；依次类推，第l+1层至少有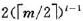个结点。而l+1层为叶子结点。若m阶B-树中具有N个关键字，则叶子结点即查找不成功的结点为N+1，由此有：

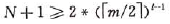 ，  即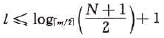

　　所以，在含有N个关键字的m阶B-树上进行查找时，从根结点到关键字所在结点的路径上涉及的结点数不超过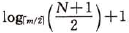

 

代码实现

略