查找->动态查找表->二叉排序树

 文字描述

　　二叉排序树的定义

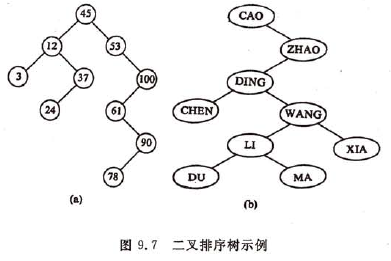
　　又称二叉查找树，英文名为Binary Sort Tree, 简称BST。它是这样一棵树：或者是一棵空树；或者是具有下列性质的二叉树：(1)若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；(2)若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；(3)它的左、右子树也分别是二叉排序树。

　　二叉排序树的查找

　　其查找过程和次优二叉树类似。即当二叉排序树不为空时，首先将给定值和根结点的关键字比较，若相等，则查找成功，否则将依据给定值和根结点的关键字之间的大小关系，分别在左子树或右子树上继续进行查找。

　　二叉排序树的插入

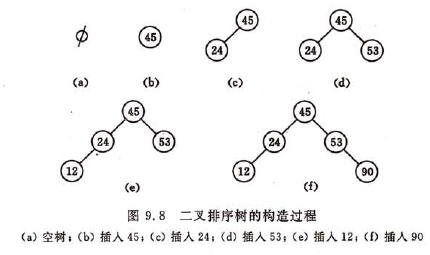
　　和次优查找树相对，次优查找树是一种静态查找表。而二叉排序树是一种动态树表，其特点是，树的结构通常不是一次生成的，而是在查找过程中，当树中不存在关键字等于给定值的结点时再进行插入。新插入的结点一定是一个新添加的叶子结点，并且是查找不成功时查找路径上访问的最后一个结点的左孩子或右孩子结点。

　　二叉排序树的删除

　　在二叉排序树上删除一个结点相当于删除有序序列中的一个纪录，只要在删除某个结点之后依旧保持二叉排序树的特性即可。假设被删除结点*p(指向结点的指针为p)，其双亲结点*f(结点类型为f)，且不失一般性，可设*p是*f的左孩子。下面分3种情况进行讨论：

　　(1)若*p结点为叶子结点，即PL和PR均为空树。由于删除叶子结点*p不破坏整棵树的结构，则只需修改其双亲结点的指针即可。

　　(2)若*p结点只有左子树PL或只有右子树PR，此书只要令PL或PR直接成为其双亲结点*f的左子树即可。

　　(3)若*p结点的左子树和右子树均不为空。从下图知，在删除*p之前，中序遍历该二叉树的序列为{…C_LC…Q_LQS_LSPP_RF…}, 在删除*p之后，为保持其他元素之间的相对位置不变，可以有两种方法：[3.1]令*p的左子树为*f的左子树，而*p的右子树为*s的右子树。如下图(c)所示。[3.2]另*p的直接前驱(或直接后继)替代*p，然后再从二叉排序树中删去它的直接前驱(或直接后继)。如下图(d)所示，当以直接前驱*s替代*p时，由于*s只有左子树S_L，则在删除*s之后，只要令S_L为*s的双亲*q的右子树即可。

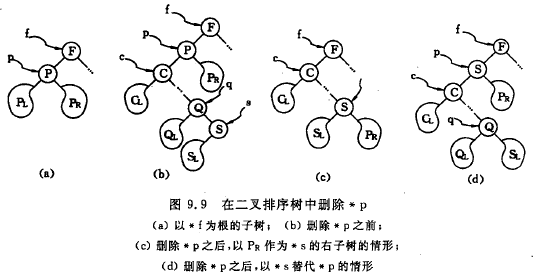
示意图

 

算法分析

　　和折半查找类似，与给定值比较的关键字个数不超过树的深度。然而，折半查找长度为n的表的判定树是惟一的，而含有n个结点的二叉排序树却不惟一。因此，含有n个结点的二叉排序树的平均查找长度和树的形态有关。

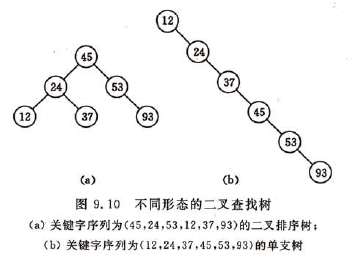
　　当先后插入的关键字有序时，构成的二叉排序树蜕变成单支树。树深度为n，其平均查找长度为(n+1)/2，和顺序查找相同，这是最差情况。

　　最好的情况是二叉排序树的形态和折半查找的判定树相同，其平均查找长度和log₂n成正比。

　　假设含有n(n>=1)个关键字的序列中，查找概率相等的情况下，其平均查找长度如下图，由此可见，在随机情况下，二叉排序树的平均查找长度和logn是等数量级的。

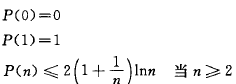
代码实现

//./a.out 45 12 53 3 37 100 24 61 90 78

//测试
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define DEBUG

#define MAX_SIZE 50
#define TRUE  1
#define FALSE 0

#define EQ(a, b) ((a)==(b))
#define LT(a, b) ((a)< (b))
#define LQ(a, b) ((a)<=(b))

/*定义关键字key为int型*/
typedef int KeyType;
/*数据元素类型*/
typedef struct{
    KeyType key;
}ElemType;
/*二叉链表结构*/
typedef struct{
    ElemType data;
    struct BiTNode *lchild;
    struct BiTNode *rchild;
}BiTNode, *BiTree;

/*二叉排序树查找算法
 *
 *在根指针T所指二叉排序树中递归地查找其关键字等于key。
 *若查找成功，则指针p指向该数据元素结点，指针f2指向p的父亲结点，并返回TRUE
 *若查找失败，则指针p指向查找路径上访问的最后一个结点，并返回FALSE。
 *
 *注意：
 *指针f是传入参数，指向T的双亲，其初始调用值为NULL
 *指针f2是传出参数，若查找成功，则指向p的父亲结点
 */
int SearchBST(BiTree T, KeyType key, BiTree f, BiTree *p, BiTree *f2){
    if(!T){
        //查找不成功
        *p = f;
        return FALSE;
    }else if(EQ(key, T->data.key)){
        //查找成功
        *p = T;
        //f2指向结点p的父亲结点
        if(f2){
            *f2 = f;
        }
        return TRUE;
    }else if(LT(key, T->data.key)){
        //在左子树上继续查找
        return SearchBST((BiTree)T->lchild, key, T, p, f2);
    }else{
        //在右子树上继续查找
        return SearchBST((BiTree)T->rchild, key, T, p, f2);
    }
}

/*二叉排序树插入算法
 *
 *当二叉排序树T中不存在关键字等于e.key的数据元素时，插入e并返回TRUE，否则返回FALSE。
 */
int InsertBST(BiTree *T, ElemType e){
    //提示：这儿必须用malloc给p分配堆，否则调用的SearchBST函数里无法给*p赋值。
    BiTree *p = (BiTree*)malloc(sizeof(BiTree*));
    if(!SearchBST(*T, e.key, NULL, p, NULL)){
        //查找不成功，所以不存在关键字等于e.key的数据元素，需要插入
        BiTree s = (BiTree)malloc(sizeof(BiTNode));
        s->data = e;
        s->lchild = s->rchild = NULL;
        if(!(*p)){
            //被插结点*s为新的根结点
            *T = s;
        }else if(LT(e.key, (*p)->data.key)){
            //被插结点*s为左孩子
            (*p)->lchild = s;
        }else{
            //被插结点*s为右孩子
            (*p)->rchild = s;
        }
        free(p);
        return FALSE;
    }else{
        //查找成功，说明树中已有关键字相同的结点，不需要再插入。
        free(p);
        return TRUE;
    }
}

/*二叉排序树删除算法
 *
 *若二叉排序树T中存在关键字等于key的数据元素，则删除该数据元素结点，并返回TRUE。
 *否则返回FALSE
 */
int DeleteBST(BiTree *T, KeyType key){
    int ret = FALSE;
    
    BiTree *p = (BiTree*)malloc(sizeof(BiTree*));
    BiTree *father = (BiTree*)malloc(sizeof(BiTree*));
    
    if(SearchBST(*T, key, NULL, p, father)){
        //找到关键字等于key的数据元素，需要删除
        
        if(!(*p)->lchild){
            //左子树空，则只需重接它的右子树
            
            if(*father){
                //被删结点不是根结点，因为其父亲结点father非空
                if((*p) == (BiTree)(*father)->lchild){
                    //被删结点是其父亲结点的左子树
                    (*father)->lchild = (*p)->rchild;
                }else{
                    //被删结点是其父亲结点的右子树
                    (*father)->rchild = (*p)->rchild;
                }
            }else{
                //被删结点是根结点，因为其父亲结点father空
                *T = (BiTree)((*p)->rchild);
            }
            free(*p);
            *p = NULL;
        }else if(!(*p)->rchild){
            //右子树空，则只需重接它的左子树
            
            if(*father){
                //被删结点不是根结点，因为其父亲结点father非空
                if((*p) == (BiTree)(*father)->lchild){
                    //被删结点是其父亲结点的左子树
                    (*father)->lchild = (*p)->lchild;
                }else{
                    //被删结点是其父亲结点的右子树
                    (*father)->rchild = (*p)->lchild;
                }
            }else{
                //被删结点不是根结点，因为其父亲结点father空
                *T = (BiTree)((*p)->lchild);
            }
            free(*p);
            *p = NULL;
        }else{    
            //左右子树都不为空
            BiTNode *q, *s;
            q = (BiTNode*)*p;
            //转左
            s = (BiTNode*)(*p)->lchild;
            //然后向右走到尽头
            while(s->rchild){
                q = s;
                s = (BiTNode*)s->rchild;
            }
            //s指向被删除结点的"前驱"
            (*p)->data = s->data;
            if(q!=(BiTNode*)(*p)){
                //重接*q的右子树
                q->rchild = s->lchild;
            }else{
                //重接*q的左子树
                q->lchild = s->lchild;
            }
            free(s);
        }

        ret = TRUE;
    }else{
        //不存在关键字等于key的数据元素，不需要删除，返回FALSE。
        ret = FALSE;
    }
    free(p);
    free(father);
    return ret;
}

/*先序遍历二叉树算法声明*/
int PreOrderTraverse(BiTree T);    
/*中序遍历二叉树算法声明*/
int InOrderTraverse(BiTree T);    
/*后序遍历二叉树算法声明*/
int PostOrderTraverse(BiTree T);

/*分别用先、中、后序遍历算法顺序打印二叉排序树*/
void print(BiTree T)
{
    printf("先序遍历二叉排序树:\n");
    PreOrderTraverse(T);
    printf("\n");

    printf("中序遍历二叉排序树:\n");
    InOrderTraverse(T);
    printf("\n");

    printf("后序遍历二叉排序树:\n");
    PostOrderTraverse(T);
    printf("\n");
}

int main(int argc, char *argv[])
{
    if(argc < 2)
        return FALSE;
    int i = 0;
    BiTree T = NULL;
    ElemType e;
    //动态创建二叉排序树
    for(i=1; i<argc; i++){
        e.key = atoi(argv[i]);
        //如果元素e不存在，就插入到二叉排序树T中
        InsertBST(&T, e);
    }
#ifdef DEBUG
    print(T);
#endif

    KeyType k = 0;
    while(1){
        printf("\n输入要删除的key(负值表示结束):");
        scanf("%d", &k);
        if(k<0)
            break;
        if(DeleteBST(&T, k)){
            printf("删除key(%d)成功!!!!!!\n", k);
#ifdef DEBUG
            print(T);
#endif
        }else{
            printf("删除key(%d)失败!!!!!!\n", k);
        }
    }
    return 0;
}

/*先序遍历二叉树算法实现*/
int PreOrderTraverse(BiTree T){
    if(T){
        printf("%d  ", ((BiTNode*)T)->data.key);
        PreOrderTraverse((BiTree)T->lchild);
        PreOrderTraverse((BiTree)T->rchild);
    }
    return 0;
}

/*中序遍历二叉树算法实现*/
int InOrderTraverse(BiTree T){
    if(T){
        InOrderTraverse((BiTree)T->lchild);
        printf("%d  ", ((BiTNode*)T)->data.key);
        InOrderTraverse((BiTree)T->rchild);
    }
    return 0;
}

/*后序遍历二叉树算法实现*/
int PostOrderTraverse(BiTree T){
    if(T){
        PostOrderTraverse((BiTree)T->lchild);
        PostOrderTraverse((BiTree)T->rchild);
        printf("%d  ", ((BiTNode*)T)->data.key);
    }
    return 0;
}

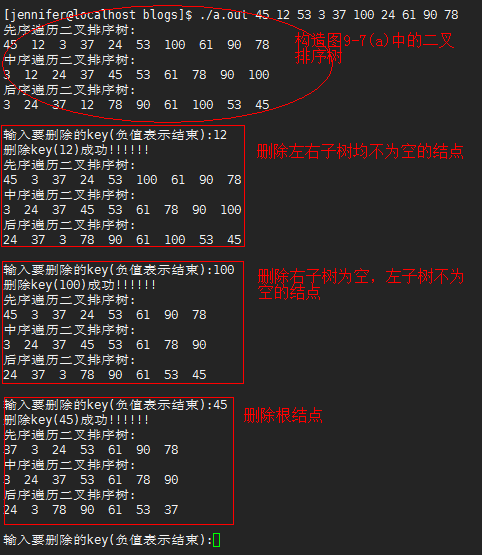
运行