查找->静态查找表->次优查找(静态树表)

文字描算

　　之前分析顺序查找和折半查找的算法性能都是在“等概率”的前提下进行的，但是如果有序表中各记录的查找概率不等呢？换句话说，概率不等的情况下，描述查找过程的判定树为何类二叉树，其查找性能最佳？

　　如果只考虑查找成功的情况，则使查找性能达最佳的判定树是其带权内路径长度之和PH值取最小的二叉树。

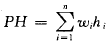
　　其中n为二叉树上结点的个数(即有序表的长度)；hi为第i个结点在二叉树上的层次数；结点的权w_i=cpi(i=1,2,…,n)，其中pi为结点的查找概率，c为某个常量。称PH值取最小的二叉树为静态最优查找树。由于构造静态最优查找树代价较高，在此介绍一种构造近似最优查找树的有效算法。该算法的过程描述如下：

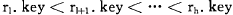　　已知一个按关键字有序的记录序列,其中, 与每个记录相应的权值为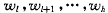

 

　　首先在记录序列中取第i(l<=i && i<=h)个记录构造根结点，使得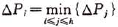取最小值，然后分别对子序列和构造两棵次优查找树，并分别设为根结点的左子树和右子树。 

 

示意图

 

 

算法分析

　　从次优查找树的结构特定可知，其查找过程类似于折半查找。查找过程和二叉排序树算法类型，待二叉排序树会讲。由于查找过程是走了一条从根到待查记录所在节点(或叶子结点)的一条路径，进行过比较的关键字个数不超过树的深度，因此，次优查找树的平均查找长度和logn成正比。可见，在记录的查找概率不等时，可用次优查找树表示静态查找表，故又称为静态树表。

       另外，大量实验表明，次优查找树和最优查找树的查找性能之差仅仅为1%-2%，很少查过3%，而且构造次优查找树的算法的时间复杂度为nlogn。

代码实现

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define DEBUG
#define EQ(a, b) ((a)==(b))
#define LT(a, b) ((a)< (b))
#define LQ(a, b) ((a)<=(b))
#define MAX_SIZE 50

typedef char KeyType;
//数据元素类型
typedef struct{
    //关键字
    KeyType key;
    //权值
    int weight;
}ElemType;
//静态查找表
typedef struct{
    //数据元素存储空间基址,0号单元留空
    ElemType *elem;
    //表长度
    int length;
}SSTable;
//二叉链表, 次优查找树采用二叉链表的存储结构
typedef struct{
    ElemType data;
    struct BiTNode *lchild;
    struct BiTNode *rchild;
}BiTNode, *BiTree;

//由有序表R[low,...,high]及累计权值表sw(其中sw[0]==0)递归构造次优查找树T
BiTNode* SecondOptimal(ElemType R[], int sw[], int low, int high)
{
    int i = low, j = 0;
    int min = abs(sw[high]-sw[low]);
    int dw = sw[high]+sw[low-1];
    //选择最小的<>Pi值
    for(j=low+1; j<=high; ++j){
        if(abs(dw-sw[j]-sw[j-1])<min){
            i = j;
            min = abs(dw-sw[j]-sw[j-1]);
        }
    }
#ifdef DEBUG
    printf("i=%d, low=%d, high=%d\n", i, low, high);
#endif
    //生成结点
    BiTNode* T = (BiTNode*)malloc(sizeof(BiTNode));
    T->data = R[i];
    T->lchild = T->rchild = NULL;
    if(i==low){
        //左子树空
        T->lchild = NULL;
    }else{
        //构造左子树
        T->lchild = SecondOptimal(R, sw, low, i-1);
    }
    if(i==high){
        //右子树空
        T->rchild = NULL;
    }else{
        //构造右子树
        T->rchild = SecondOptimal(R, sw, i+1, high);
    }
    return T;
}

//按照由有序表ST中各数据元素的weight域求累计权值表sw
void FindSW(int sw[], SSTable ST)
{
    int i = 1;
    sw[0] = 0;
    for(i=1; i<=ST.length; i++){
        sw[i] = sw[i-1]+ST.elem[i].weight;
    }
#ifdef DEBUG
    printf("SW  : ");
    for(i=1; i<=ST.length; i++){
        printf("[%d]=%-3d  ", i, sw[i]);
    }
    printf("\n");
#endif
    return ;
}

//由有序表ST构造一棵次优查找树. ST的数据元素含有权域weight
BiTree CreateSOSTree(SSTable ST)
{
    if(ST.length == 0)
        return NULL;
    else{
        int sw[MAX_SIZE+1] = {0};
        //按照由有序表ST中各数据元素的weight域求累计权值表sw
        FindSW(sw, ST);
        //由有序表ST.elem[low,...,high]及累计权值表sw(其中sw[0]==0)递归构造次优查找树并返回
        return (BiTree)SecondOptimal(ST.elem, sw, 1, ST.length);
    }
}

//顺序打印有序表ST中的数据元素。
void print(SSTable SS){
    printf("data: ");
    int i = 0;
    for(i=1; i<=SS.length; i++){
        printf("[%d]=%c,%d  ", i, SS.elem[i].key, SS.elem[i].weight);
    }
    printf("\n");
}

int PreOrderTraverse(BiTree T);    //先序遍历
int InOrderTraverse(BiTree T);    //中序遍历
int PostOrderTraverse(BiTree T);//后序遍历

int main(int argc, char *argv[])
{
    
    KeyType key;
    int weight;
    int i = 1;
    char tmp[10] = {0};
#ifdef DEBUG
    ElemType arr[MAX_SIZE+1] = {{'0',0},{'A',1}, {'B',1}, {'C',2}, {'D',5}, {'E',3},{'F',4},{'G',4},{'H',3},{'I',5},};
    i = 10;
#else
    ElemType arr[MAX_SIZE+1];
    while(1){
        printf("输入 关键字,权值('0,0'是结束):");
        memset(tmp, 0, sizeof(tmp));
        scanf("%s", tmp);
        sscanf(tmp, "%c,%d", &key, &weight);
        if(key == '0' && weight ==0){
            break;
        }else{
            arr[i].key = key;
            arr[i].weight = weight;
            i+=1;
        }
    }
#endif
    SSTable SS;
    SS.elem = arr;
    SS.length = i-1;
#ifdef DEBUG
    print(SS);
#endif
    BiTree T = CreateSOSTree(SS);
    printf("先序遍历:");
    PreOrderTraverse(T);
    printf("\n");
    
    printf("中序遍历:");
    InOrderTraverse(T);
    printf("\n");
    
    printf("后序遍历:");
    PostOrderTraverse(T);
    printf("\n");
    return 0;
}

int PreOrderTraverse(BiTree T){
    if(T){
        printf("%c,%d  ", ((BiTNode*)T)->data.key, ((BiTNode*)T)->data.weight);
        PreOrderTraverse((BiTree)T->lchild);
        PreOrderTraverse((BiTree)T->rchild);
    }
    return 0;
}

int InOrderTraverse(BiTree T){
    if(T){
        InOrderTraverse((BiTree)T->lchild);
        printf("%c,%d  ", ((BiTNode*)T)->data.key, ((BiTNode*)T)->data.weight);
        InOrderTraverse((BiTree)T->rchild);
    }
    return 0;
}

int PostOrderTraverse(BiTree T){
    if(T){
        PostOrderTraverse((BiTree)T->lchild);
        PostOrderTraverse((BiTree)T->rchild);
        printf("%c,%d  ", ((BiTNode*)T)->data.key, ((BiTNode*)T)->data.weight);
    }
    return 0;
}

 

运行