树和二叉树->线索二叉树

文字描述

　　从二叉树的遍历可知，遍历二叉树的输出结果可看成一个线性队列，使得每个结点(除第一个和最后一个外)在这个线形队列中有且仅有一个前驱和一个后继。但是当采用二叉链表作为二叉树的存储结构时，只能得到结点的左孩子结点和右孩子结点，要想知道结点的前驱或后继，需要再遍历一次才知道。另外，叶子结点的左右孩子结点是空链域，在有n个结点的二叉链表中必定存在n+1个空链域，原因见[附录1证明]。由此，便可以考虑利用这些叶子结点的空链域来存放结点的前驱和后继结点。

　　线索二叉树的存储结构中增加两个标志域LTag和RTag，标志左/右链域是孩子结点还是前驱或后继。这种存储结构叫做线索存储，之前前驱和后继的结点指针叫线索，加上线索的二叉树叫线索二叉树。关于线索二叉树主要有两个问题需要解决：

　　第一个问题如何建立线索二叉树？

　　第二个问题如何遍历线索二叉树？

　　第一个问题：如何建立线索二叉树？

　　线索化的实质就是将二叉链表的空指针改为前驱或后继的线索。而前驱或后继的信息只有在遍历时才能得到，因此线索化的过程即为在遍历过程中修改空指针的过程。为了记下遍历过程中访问结点的先后关系，附设一个pre始终指向刚刚访问过的结点，若指针p指向当前访问的结点，则pre就是p的前去，p就是pre的后继。

　　第二个问题：如何遍历线索二叉树？

　　在线索树上遍历，只要先找到序列中的第一个结点，然后依次找结点后继直至后继为空时为止。树中所有叶子结点的链域就是线索，左链指示了该结点的前驱，右链域指示了该结点的后继，而如何在线索树中找非叶子结点的前驱或后继呢？

　　对于先序线索树根据先序遍历的规律知，非终端结点的后继：如果其左孩子存在,则后继就是其左孩子结点. 否则后继就是其右孩子结点.

　　对于中序线索树根据中序遍历的规律知，。非终端结点的后继应该是遍历其右子树时访问的第一个结点，即右子树中最左下的结点；

　　对于后序线索树在后序线索树中找结点后继复杂些，分3种情况: (1)若结点x是二叉树的根，其后继就是为空；(2)若结点x是其双亲结点的右孩子或者是其双亲的左孩子且其双亲没有右子树，则其后继即为双亲结点 (3)若结点x是其双亲的左孩子，且双亲有右子树，则其后继为双亲的右子树上按后序遍历列出的第一个结点。可见，在后序线索树上找后继时需知道结点双亲，即需带标志域的三叉链表作存储结构。

示意图

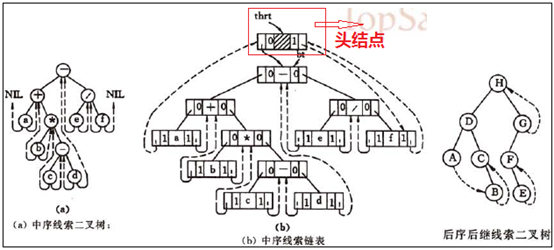
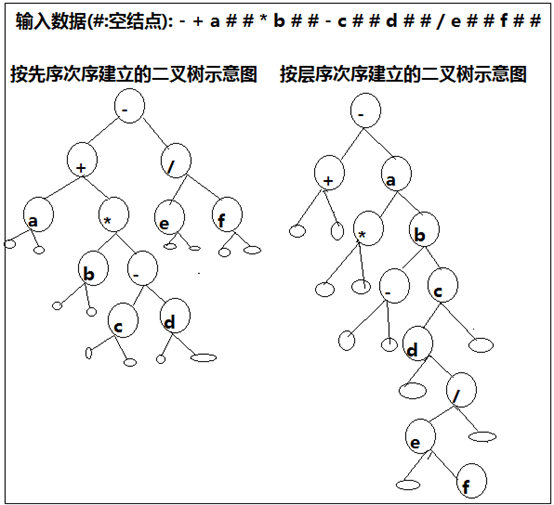
算法分析

　　线索二叉树上遍历二叉树，时间复杂度仍然为n，但是常数因子要比非线索二叉树的遍历算法小，且不需要另外设栈或队列。因此，若二叉树需要经常遍历或查找结点在遍历所得线性序列中的前驱和后继，则应采用线索链表做存储结构。

代码实现

  1 /*
  2  *
  3  * 编译本文件后，可输入如下参数:
  4  *
  5  * ./a.out - + a \# \# \* b \# \# - c \# \# d \# \# / e \# \# f \# \# 
  6  *
  7  */
  8 
  9 #include <stdio.h>
 10 #include <stdlib.h>
 11 
 12 
 13 #define DEBUG
 14 #define EQ(a, b) ((a)==(b))
 15 /*树中结点的最大个数*/
 16 #define MAX_TREE_SIZE 100
 17 
 18 typedef char KeyType;
 19 typedef int InfoType;
 20 
 21 /*树中的结点类型*/
 22 typedef struct{
 23     KeyType key;
 24     InfoType otherinfo;
 25 }TElemType;
 26 
 27 /*Link==0指针，Thread==1线索*/
 28 typedef enum PointerTag{Link=0, Thread}PointerTag; 
 29 
 30 /*
 31  * 二叉树的二叉线索存储表示
 32  *
 33  * 链表中的结点包含五个数据：数据域data，左指针域lchild，右指针域rchild, 左标志, 右标志
 34  */
 35 typedef struct BiTNode{
 36     TElemType data;
 37     struct BiTNode *lchild, *rchild;
 38     PointerTag LTag, RTag;
 39 }BiThrNode, *BiThrTree;
 40 
 41 /* 
 42  * 创建二叉链表
 43  *
 44  * 按先根次序输入二叉树中结点的值，'#'表示空结点
 45  * 构造二叉链表表示的二叉树T
 46  */
 47 int I = 0;
 48 BiThrTree CreateBiTree(TElemType input[]){
 49     TElemType data = input[I++];
 50     BiThrTree T = NULL;
 51     if(data.key == '#'){
 52         T = NULL;
 53         return T;
 54     }else{
 55         if(!(T=(BiThrNode *)malloc(sizeof(BiThrNode)))){
 56             printf("Error: overflow!\n");
 57             exit(1);
 58         }
 59         T->data = data;
 60         T->lchild = CreateBiTree(input);
 61         T->rchild = CreateBiTree(input);
 62         return T;
 63     }
 64 }
 65 
 66 /*遍历二叉树时用到的函数指针参数*/
 67 int vist(TElemType e){
 68     printf("%c ", e.key);
 69     return 0;
 70 }
 71 
 72 /*
 73  * pre总指向刚刚访问过的结点，
 74  * 若p指向刚刚访问过的结点，则pre指向它的前驱；p指向pre的后继。
 75  */
 76 BiThrTree pre;
 77 
 78 
 79 
 80 
 81 
 82 
 83 
 84 
 85 
 86 
 87 //////////////////////////////////////////////////////////////////////////////////
 88 //先序线索二叉树的遍历与建立-start////////////////////////////////////////////////
 89  
 90 int PreOrderTraverse_Thr(BiThrTree Thrt, int (*fun)(TElemType e)){
 91     BiThrTree p = Thrt->lchild;
 92     while(p!=Thrt){
 93         fun(p->data);
 94         while(p->LTag == Link){
 95             p = p->lchild;
 96             fun(p->data);
 97         }
 98         p = p->rchild;
 99     }
100     return 0;
101 }
102 
103 /*先序线索二叉树的建立*/
104 void PreThreading(BiThrTree p){
105     if(p){
106         if(!p->lchild){
107             p->LTag = Thread;
108             p->lchild = pre;
109         }
110         if(!pre->rchild){
111             pre->RTag = Thread;
112             pre->rchild = p;
113         }
114         pre = p;
115         if(p->LTag == Link)
116             PreThreading(p->lchild);
117         if(p->RTag == Link)
118             PreThreading(p->rchild);
119     }
120     return ;
121 }
122 
123 /*先序线索二叉树的建立*/
124 BiThrTree PreOrderThreading(BiThrTree T){
125     //建立头指针
126     BiThrTree Thrt = NULL;
127     if(!(Thrt=(BiThrTree)malloc(sizeof(BiThrNode)))){
128         printf("malloc fail!\n");
129         return NULL;
130     }
131     Thrt->LTag = Link;
132     //右指针回值
133     Thrt->RTag = Thread;
134     Thrt->rchild = Thrt;
135     if(!T){
136         //若二叉树空，则右指针回指
137         Thrt->lchild = Thrt;
138     }else{
139         Thrt->lchild = T;
140         pre = Thrt;
141         //中序线索化
142         PreThreading(T);
143         //最后一个结点线索化
144         pre->RTag = Thread;
145         pre->rchild = Thrt;
146         Thrt->rchild = pre;
147     }
148     return Thrt;
149 }
150 
151 //先序线索二叉树的遍历与建立-end///////////////////////////////////////////////
152 ///////////////////////////////////////////////////////////////////////////////
153 
154 
155 
156 
157 
158 
159 
160 
161 
162 
163 //////////////////////////////////////////////////////////////////////////////////
164 //中序线索二叉树的遍历与建立-start////////////////////////////////////////////////
165  void InThreading(BiThrTree p){
166     if(p){
167         //左子树线索化
168         InThreading(p->lchild);
169         //pre指向p的前驱
170         if(!p->lchild){
171             p->LTag = Thread;
172             p->lchild = pre;
173         }
174         //p指向pre的后继
175         if(!pre->rchild){
176             pre->RTag = Thread;
177             pre->rchild = p;
178         }
179         //保持pre指向p的前驱
180         pre = p;
181         //右子树线索化
182         InThreading(p->rchild);
183     }
184     return ;
185 }
186 
187 /*
188  * 中序线索二叉树的建立
189  *
190  * 中序遍历二叉树T,并将其中序线索化，返回值指向线索化的头结点
191  * 头结点的lchild域的指针指向二叉树的根结点，其rchild域的指针指向中序遍历时访问的最后一个结点；
192  * 另外，令二叉树中序序列中的第一个结点的lchild域指针和最后一个结点rchild域的指针均指向头结点。
193  */
194 BiThrTree InOrderThreading(BiThrTree T){
195     //建立头指针
196     BiThrTree Thrt = NULL;
197     if(!(Thrt=(BiThrTree)malloc(sizeof(BiThrNode)))){
198         printf("malloc fail!\n");
199         return NULL;
200     }
201     Thrt->LTag = Link;
202     //右指针回值
203     Thrt->RTag = Thread;
204     Thrt->rchild = Thrt;
205     if(!T){
206         //若二叉树空，则右指针回指
207         Thrt->lchild = Thrt;
208     }else{
209         Thrt->lchild = T;
210         //pre总指向刚刚访问过的结点，若p指向刚刚访问过的结点，则pre指向它的前驱；p指向pre的后继。
211         pre = Thrt;
212         //中序遍历进行中序线索化
213         InThreading(T);
214         //最后一个结点线索化
215         pre->RTag = Thread;
216         pre->rchild = Thrt;
217         Thrt->rchild = pre;
218     }
219     return Thrt;
220 }
221 
222 /*
223  * 中序线索二叉树的遍历
224  */
225 int InOrderTraverse_Thr(BiThrTree Thrt, int (*fun)(TElemType e)){
226     BiThrTree p = Thrt->lchild;
227     while(p!=Thrt){
228         while(p->LTag==Link) p = p->lchild;
229         fun(p->data);
230         while(p->RTag==Thread && p->rchild != Thrt){
231             p = p->rchild;
232             fun(p->data);
233         }
234         p = p->rchild;
235     }
236     return 0;
237 }
238 //中序线索二叉树的遍历与建立-end//////////////////////////////////////////////////
239 //////////////////////////////////////////////////////////////////////////////////
240 
241 
242 
243 
244 
245 
246 
247 
248 
249 
250 
251 //////////////////////////////////////////////////////////////////////////////////
252 //后序线索二叉树的遍历与建立-start///////////////////////////////////////////////
253 /*三叉链表结构*/
254 typedef struct BiPTNode{
255     TElemType data;
256     struct BiPTNode *lchild, *rchild, *parent;
257     PointerTag LTag, RTag;
258 }BiPThrNode, *BiPThrTree;
259 
260 ////////////////////////////////////////
261 //与队列相关的结构体和函数声明-start////
262 typedef struct QNode{
263     BiPThrTree data;
264     struct QNode *next;
265 }QNode, *QuenePtr;
266 
267 typedef struct{
268     QuenePtr front;
269     QuenePtr rear;
270 }LinkQueue;
271 
272 LinkQueue* InitQueue(void);
273 int QueueEmpty(LinkQueue *Q);
274 int GetHead(LinkQueue *Q, BiPThrTree *e);
275 int EnQueue(LinkQueue *Q, BiPThrTree *e);
276 int DeQueue(LinkQueue *Q, BiPThrTree *e);
277 //与队列相关的结构体和函数声明-end////////
278 //////////////////////////////////////////
279 
280 /*
281  * 三叉链表的建立
282  * 
283  * 按照层序遍历的顺序依次输入结点input， 然后建立带双亲结点的三叉链表。
284  *
285  */
286 BiPThrTree CreatePBiTree(TElemType input[]){
287     I = 0;
288     TElemType data;
289     BiPThrTree PT = NULL, parent, lchild=NULL, rchild=NULL;
290     if((data=input[I++]).key == '#'){
291         return PT;
292     }else{
293         if(!(PT=(BiPThrNode *)malloc(sizeof(BiPThrNode)))){
294             exit(1);
295         }
296         PT->data = data;
297         PT->parent = NULL;
298         LinkQueue *Q = InitQueue();
299         EnQueue(Q, &PT);
300         while(QueueEmpty(Q)){
301             DeQueue(Q, &parent);
302             if((data=input[I++]).key == '#'){
303                 lchild = NULL;
304             }else{
305                 lchild = (BiPThrNode *)malloc(sizeof(BiPThrNode));
306                 lchild->data = data;
307                 lchild->parent = parent;
308                 EnQueue(Q, &lchild);
309             }
310             (parent)->lchild = lchild;
311 
312             if((data=input[I++]).key == '#'){
313                 rchild = NULL;
314             }else{
315                 rchild = (BiPThrNode *)malloc(sizeof(BiPThrNode));
316                 rchild->data = data;
317                 rchild->parent = parent;
318                 EnQueue(Q, &rchild);
319             }
320             (parent)->rchild = rchild;
321         }
322     }
323     return PT;
324 }
325 
326 /*
327  * pre_p总指向刚刚访问过的结点，
328  * 若p指向刚刚访问过的结点，则pre_p指向它的前驱；p指向pre_p的后继。
329  */
330 BiPThrTree pre_p;
331 
332 void PostThreading(BiPThrTree p){
333     if(p){
334         PostThreading(p->lchild);
335         PostThreading(p->rchild);
336         if(!p->lchild){
337             p->LTag = Thread;
338             p->lchild = pre_p;
339         }
340         if(!pre_p->rchild){
341             pre_p->RTag = Thread;
342             pre_p->rchild = p;
343         }
344         pre_p = p;
345     }
346     return ;
347 }
348 
349 /*后序线索二叉树的建立*/
350 BiPThrTree PostOrderThreading(BiPThrTree T){
351     BiPThrTree Thrt = NULL;
352     if(!(Thrt=(BiPThrTree)malloc(sizeof(BiPThrNode)))){
353         return NULL;
354     }
355     Thrt->LTag = Link;
356     Thrt->RTag = Thread;
357     Thrt->rchild = Thrt;
358     if(!T){
359         Thrt->lchild = Thrt;
360     }else{
361         Thrt->lchild = T;
362         pre_p = Thrt;
363         PostThreading(T);
364         pre_p->RTag = Thread;
365         pre_p->rchild = Thrt;
366         Thrt->rchild = pre_p;
367     }
368 }
369 
370 /*后序线索二叉树的遍历*/
371 void PostOrderTraverse_Thr(BiPThrTree Thrt, int (*fun)(TElemType e))
372 {
373     BiPThrTree p = Thrt->lchild;
374     while(p->LTag == Link){
375         p = p->lchild;
376     }
377     while(p!=Thrt){
378         fun(p->data);
379         while(p->RTag==Thread && p->rchild != Thrt){
380             p = p->rchild;
381             fun(p->data);
382         }
383         if(p->parent){
384             p = p->parent;
385         }else{
386             break;
387 
388         }
389     }
390 }
391 //后序线索二叉树的遍历与建立-end//////////////////////////////////////////////////
392 //////////////////////////////////////////////////////////////////////////////////
393 
394 
395 
396 
397 int main(int argc, char *argv[])
398 {
399     if(argc < 2) 
400         return -1;
401 
402     TElemType input[MAX_TREE_SIZE];
403     int i = 0, j = 0;
404     for(i=0; i<MAX_TREE_SIZE; i++){
405         input[i].key = '#';
406     }
407 
408     //按先根次序输入二叉树中结点的值，'#'表示空树
409     for(i=1; i<argc; i++){
410         if(i>MAX_TREE_SIZE)
411             break;
412         input[i-1].key = argv[i][0];
413         input[i-1].otherinfo = i-1;
414     }
415 #ifdef DEBUG
416     printf("输入数据以建立二叉树(#表示空空结点):\n");
417     for(j=0; j< i-1; j++){
418         printf("%c ", input[j].key);
419     }
420     printf("\n");
421 #endif
422     printf("先序线索二叉树的建立与遍历:(按照先序次序建立二叉树)\n");
423     I=0;
424     BiThrTree PreT = CreateBiTree(input);
425     BiThrTree PreThrt = PreOrderThreading(PreT);
426     PreOrderTraverse_Thr(PreThrt, vist);
427     
428     printf("\n中序线索二叉树的建立与遍历:(按照先序次序建立二叉树)\n");
429     I = 0;
430     BiThrTree InT = CreateBiTree(input);
431     BiThrTree InThrt = InOrderThreading(InT);
432     InOrderTraverse_Thr(InThrt, vist);
433 
434     printf("\n后序线索二叉树的建立与遍历:(按照层序次序建立二叉树)\n");
435     I=0;
436     BiPThrTree PostT = CreatePBiTree(input);
437     BiPThrTree PostThrt = PostOrderThreading(PostT);
438     PostOrderTraverse_Thr(PostThrt, vist);
439     printf("\n");
440     return 0;
441 }
442 
443 
444 
445 
446 
447 //////////////////////////////////////////////////////////////////////////////////
448 //与队列相关的函数的实现-start///////////////////////////////////////////////////
449 LinkQueue* InitQueue(void)
450 {
451     LinkQueue *Q = (LinkQueue*)malloc(sizeof(LinkQueue));
452     Q->front = Q->rear = (QuenePtr)malloc(sizeof(QNode));
453     if(!Q->front){
454         printf("malloc fail!\n");
455         return NULL;
456     }
457     return Q;
458 }
459 
460 int QueueEmpty(LinkQueue *Q)
461 {
462     if(Q->front == Q->rear){
463         return 0;
464     }else{
465         return -1;
466     }
467 }
468 
469 int GetHead(LinkQueue *Q, BiPThrTree *e)
470 {
471     if(Q->front == Q->rear){
472         return -1;
473     }
474     *e = Q->front->next->data;
475     return 0;
476 }
477 
478 int EnQueue(LinkQueue *Q, BiPThrTree *e)
479 {
480     QuenePtr p = (QuenePtr)malloc(sizeof(QNode));
481     if(!p){
482         printf("malloc fail!\n");
483         return -1;
484     }
485     p->data = *e;
486     p->next = NULL;
487     Q->rear->next = p;
488     Q->rear = p;
489     return 0;
490 }
491 
492 int DeQueue(LinkQueue *Q, BiPThrTree *e)
493 {
494     if(Q->front == Q->rear){
495         return -1;
496     }
497     QuenePtr p = Q->front->next;
498     *e = p->data;
499     Q->front->next = p->next;
500     if(p == Q->rear){
501         Q->rear = Q->front;
502     }
503     free(p);
504     return 0;
505 }
506 //与队列相关的函数的实现-end//////////////////////////////////////////////////////
507 //////////////////////////////////////////////////////////////////////////////////

线索二叉树的建立与遍历

运行

附录1

　　证明n个结点的二叉链表中必有n+1个空链域：

　　n个结点的二叉链表中共有n*2个链域，除根结点外的每个结点都有一个父亲结点，所以2*n个链域中有n-1个有内容的链域。所以共有2*n-(n-1) = n+1个空链域。

posted on 2018-08-09 18:08 LiveWithACat 阅读(332) 评论(0) 编辑收藏举报

刷新页面返回顶部

心若幽兰

树和二叉树->线索二叉树

导航

公告