图->有向无环图->求关键路径

文字描述

　　与AOV-网相对应的是AOE-网(Activity on Edge)即边表示活动的网。AOE-网是一个带权的有向无环图。其中，顶点表示事件Event，弧表示活动，权表示活动持续的时间。通常，AOE-网可用来估算工程的完成时间。

　　对AOE-网来说，研究的问题有两个：(1)完成整项工程至少需要多少时间？(2)哪些活动是影响工程进度的关键?　　

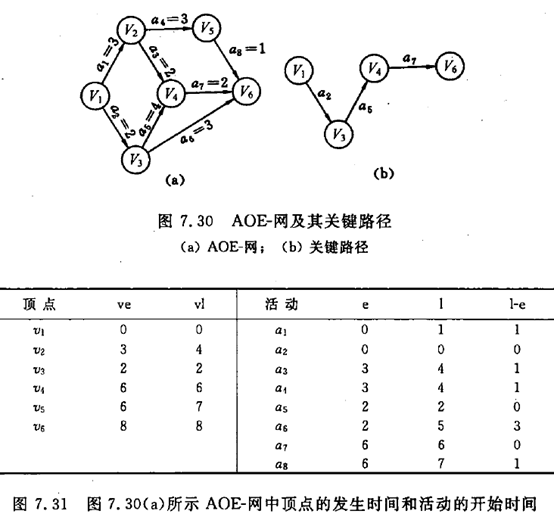
　　由于在AOE-网中有些活动可以并行地进行，所以完成工程的最短时间是从开始点到完成点的最长路径的长度(指路径上各活动持续时间之和，不是路径上弧的数目)。路径长度最长的路径叫做关键路径。

　　假设开始点是v1，从v1到vi的最长路径叫事件vi的最早发生时间。这个时间决定了所有以vi为尾的弧所表示的活动的最早开始时间。用e(i)表示活动ai的最早开始时间。用l(i)表示ai的最迟开始时间，这是在不推迟整个工程完成的前提下，活动ai最迟必须开始进行的时间。两者之差l(i)-e(i)表示活动ai的时间余量。我们把l(i)==e(i)的活动叫做关键活动。

　　显然，关键路径上的所有活动都是关键活动，因此提前完成非关键活动并不能加快工程的进度。

　　那么如何求得各个活动的最早开始时间e(i)和最晚开始时间l(i)呢？首先应求得事件的最早发生时间ve(j)和最迟发生时间vl(j)。如果活动ai由弧<j,k>表示，其持续时间记为dut(<j,k>)，则有如下关系：

　　e(i) = ve(j)

　　l(i) = vl(k) – dut(<j,k>)

　　求ve(j)和vl(j)需分两步进行：

　　　　(1)   从ve(0)=0开始向前递推

　　　　

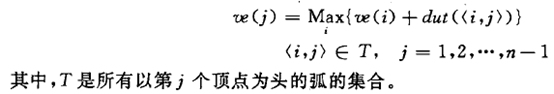
　　　　(2)   从vl(n-1)=ve(n-1)起向后递推

　　　　

　　　　这两个递推公式可以利用之前的拓扑排序算法求得。

 

示意图

 

算法分析

　　算法复杂度同拓扑排序算法，为O(n+e)。

 

代码实现

//
// Created by lady on 18-12-29.
//

#include <stdlib.h>
#include <stdio.h>
#define MAX_VERTEX_NUM 20 //最大顶点数
#define MAX_EDGE_NUM 50 //最大弧数
typedef enum {DG,DN, UDG, UDN} GraphKind; //{有向图，有向网，无向图，无向网}
typedef struct ArcNode{
    int adjvex;    //该弧所指向的顶点的位置
    struct ArcNode *nextarc;    //指向下一条弧的指针
    int info;    //该弧相关信息的指针
}ArcNode;
typedef struct VNode{
    char data[10];//顶点信息
    ArcNode *firstarcIN;//第一条以该顶点为弧头的弧结点，其他顶点->该结点
    ArcNode *firstarcOUT;//第一条以该顶点为弧尾的弧结点，该结点->其他顶点
}VNode, AdjList[MAX_VERTEX_NUM];
typedef struct{
    AdjList vertices;
    int vexnum;//图的顶点数
    int arcnum;//图的弧数
    int kind; //图的种类标志
}ALGraph;

//根据顶点信息，返回该顶点在图中的位置坐标。
int LocateVex(ALGraph *G, char data[])
{
    int i = 0;
    for(i=0; i<G->vexnum; i++){
        if(!strncmp(G->vertices[i].data, data, strlen(G->vertices[i].data))){
            return i;
        }
    }
    return -1;
}

//利用头插法，在弧结点链表头部，插入位置v的弧结点
int InsFirst(ArcNode *L, int v, int weight)
{
    if((L==NULL) || (v<0)){
        return -1;
    }
    ArcNode *n = (ArcNode *)malloc(sizeof(struct ArcNode));
    n->adjvex = v;
    n->nextarc = L->nextarc;
    n->info = weight;
    L->nextarc = n;
    return 0;
}

//采用邻接表存储方法，创建有向网，即带权的有向图
int CreateDN(ALGraph *G)
{
    printf("开始创建一个有向图,请输入顶点数，弧数:");
    int i = 0, j = 0, k = 0;
    char v1[10] = {0}, v2[10]={0}, info[10] = {0};
    char tmp[20] = {0};
    G->kind = DN;
    scanf("%d,%d", &G->vexnum, &G->arcnum);
    for(i=0; i<G->vexnum; i++){
        printf("输入第%d个顶点: ", i+1);
        memset(G->vertices[i].data, 0, sizeof(G->vertices[i].data));
        scanf("%s", G->vertices[i].data);
        G->vertices[i].firstarcOUT = (struct ArcNode *)malloc(sizeof(struct ArcNode));
        G->vertices[i].firstarcOUT->adjvex = -1;
        G->vertices[i].firstarcOUT->nextarc = NULL;
        G->vertices[i].firstarcIN = (struct ArcNode *)malloc(sizeof(struct ArcNode));
        G->vertices[i].firstarcIN->adjvex = -1;
        G->vertices[i].firstarcIN->nextarc = NULL;
    }
    for(k=0; k<G->arcnum; k++)
    {
        printf("输入第%d条弧(顶点1, 顶点2, 权值): ", k+1);
        memset(tmp, 0, sizeof(tmp));
        scanf("%s", tmp);
//      sscanf(tmp, "%[^','],%s[^\\n]", v1, v2);
        sscanf(tmp, "%[^','],%[^','],%s[^\\n]", v1, v2, info);
        i = LocateVex(G, v1);
        j = LocateVex(G, v2);
        if(i<0 || j<0){
            printf("<%s,%s> is a invalid arch!\n", v1, v2);
            return -1;
        }
        InsFirst(G->vertices[i].firstarcOUT, j, atoi((const char *)info));
        InsFirst(G->vertices[j].firstarcIN, i, atoi((const char *)info));
    }
    return 0;
}


void printG(ALGraph *G)
{
    printf("\n");
    if(G->kind == DG){
        printf("类型：有向图；顶点数 %d, 弧数 %d\n", G->vexnum, G->arcnum);
    }else if(G->kind == DN){
        printf("类型：有向网；顶点数 %d, 弧数 %d\n", G->vexnum, G->arcnum);
    }else if(G->kind == UDG){
        printf("类型：无向图；顶点数 %d, 弧数 %d\n", G->vexnum, G->arcnum);
    }else if(G->kind == UDN){
        printf("类型：无向网；顶点数 %d, 弧数 %d\n", G->vexnum, G->arcnum);
    }
    int i = 0;
    ArcNode *p = NULL;
    printf("邻接表:\n");
    for(i=0; i<G->vexnum; i++){
        printf("(%d,%s)\t", i,G->vertices[i].data);
        p = G->vertices[i].firstarcOUT;
        while(p){
            if(p->adjvex >= 0)
                printf("(%d,%s) %d\t", p->adjvex, G->vertices[p->adjvex].data, p->info);
            p = p->nextarc;
        }
        printf("\n");
    }
    printf("逆邻接表:\n");
    for(i=0; i<G->vexnum; i++){
        printf("(%d,%s)\t", i,G->vertices[i].data);
        p = G->vertices[i].firstarcIN;
        while(p){
            if(p->adjvex >= 0)
                printf("(%d,%s) %d\t", p->adjvex, G->vertices[p->adjvex].data, p->info);
            p = p->nextarc;
        }
        printf("\n");
    }
    return;
}


#define STACK_INIT_SIZE 20  //栈的初始分配量大小
#define STACK_INCREMENT 5   //栈容量不足时需新增的容量大小
typedef struct {
    int *base;  //指向栈底指针
    int *top;   //指向栈顶指针
    int stacksize;  //栈的当前容量大小
}SqStack;
int InitStack(SqStack *s);  //初始化一个栈
int StackEmpty(SqStack *s); //判断栈是否为空
int Push(SqStack *S, int *e);  //入栈函数
int Pop(SqStack *S, int *e);    //出栈函数

//算法各个顶点的入度，并将结果存放在indegree数组中
int FindInDegree(ALGraph *G, int indegree[])
{
    printf("\n对各个顶点求入度...\n");
    int i = 0;
    ArcNode *p = NULL;
    for(i=0; i<G->vexnum; i++) {
        p = G->vertices[i].firstarcIN;
        while (p) {
            if (p->adjvex >= 0) {
                indegree[i] += 1;
            }
            p = p->nextarc;
        }
    }
    for(i=0; i<G->vexnum; i++){
        printf("(%d,%s)的入度为%d\n", i, G->vertices[i].data, indegree[i]);
    }
    return 0;
}
int ve[MAX_EDGE_NUM] = {0};
int vl[MAX_EDGE_NUM] = {0};

int ToplogicalSort(ALGraph *G, SqStack *T)
{
    int i = 0;
    int j = 0;
    int k = 0;
    int count = 0;
    int indegree[MAX_VERTEX_NUM] = {0};
    ArcNode *p = NULL;
    SqStack S;
    //求各个顶点的入度
    FindInDegree(G, indegree);
    //初始化栈S，保存零入度顶点栈
    InitStack(&S);
    //将入度为0的顶点入栈S.
    for(i=0; i<G->vexnum; i++){
        if(!indegree[i]) {
            Push(&S, &i);
        }
    }
    //初始化栈T，为拓扑序列顶点栈
    InitStack(T);
    //初始化
    for(i=0; i<G->vexnum; i++){
        ve[i] = 0;
    }
    printf("\n进行拓扑排序:");
    while(StackEmpty(&S)){
        Pop(&S, &j);
        //j号顶点入T栈并计数
        Push(T, &j);
        ++count;
        printf("(%d,%s)\t", j, G->vertices[j].data);
        //对j号顶点的每个邻接点的入度减1
        for(p=G->vertices[j].firstarcOUT; p; p=p->nextarc){
            k = p->adjvex;
            if(k<0){
                continue;
            }
            //若入度为0,则入栈S
            if(!(--indegree[k])){
                Push(&S, &k);
            }
            if(ve[j]+p->info > ve[k])
                ve[k] = ve[j]+p->info;
        }
    }
    printf("\n");
    if(count<G->vexnum){
        //该有向网有环
        return -1;
    }else{
        return 0;
    }
}

//G为有向图， 输出G的各项关键活动
int CriticalPath(ALGraph *G)
{
    SqStack T;
    if(ToplogicalSort(G, &T)<0){
        return -1;
    }
    int i = 0;
    int j = 0;
    int k = 0;
    int dut = 0;
    ArcNode *p = NULL;
    //初始化顶点时间的最迟发生时间
    for(i=0; i<G->vexnum; i++){
        vl[i] = ve[i];
    }
    //按照拓扑逆序求各顶点的vl值
    while(StackEmpty(&T)){
        Pop(&T, &j);

        for(p=G->vertices[j].firstarcOUT; p; p=p->nextarc){
            k = p->adjvex;
            if(k<0)
                continue;
            dut = p->info; //dut(<j,k>)
            if(vl[k]-dut < vl[j])
                vl[j] = vl[k] - dut;
        }


        for(p=G->vertices[j].firstarcIN; p; p=p->nextarc) {
            k = p->adjvex;
            if (k < 0)
                continue;
            dut = p->info; //dut<k,j>

            if (vl[j] - dut > vl[k]) {
                vl[k] = vl[j] - dut;
            }
        }
    }
    printf("\n输出各个顶点的最早发生时间ve和最晚发生时间vl\n");
    for(i=0; i<G->vexnum; i++){
        printf("ve(%d,%s)=%d\t", i, G->vertices[i].data, ve[i]);
        printf("vl(%d,%s)=%d\n", i, G->vertices[i].data, vl[i]);
    }
    int ee = 0;
    int el = 0;
    char tag = 0;
    printf("\n输出各活动的最早发生时间ee和最晚发生时间el, *表示该活动为关键路径\n");
    for(j=0; j<G->vexnum; j++){
        for(p=G->vertices[j].firstarcOUT; p; p=p->nextarc){
            k = p->adjvex;
            if(k<0){
                continue;
            }
            dut = p->info;
            ee = ve[j];
            el = vl[k]-dut;
            tag = (ee==el)?'*':' ';
            //输出关键活动
            printf("(%d,%s)->(%d,%s), weight:%d, ee=%d, el=%d, tag=%c\n", j, G->vertices[j].data, k, G->vertices[k].data, dut, ee, el, tag);
        }
    }
    return 0;
}

int main(int argc, char *argv[])
{
    ALGraph G;
    //创建有向图
    if(CreateDN(&G)<0){
        printf("创建有向图时出错!\n");
        return -1;
    }
    //打印图
    printG(&G);
    //求关键路径
    CriticalPath(&G);
    return 0;
}


int InitStack(SqStack *S){
    S->base = (int *) malloc(STACK_INIT_SIZE * sizeof(int));
    if(!S->base){
        return -1;
    }
    S->top = S->base;
    S->stacksize = STACK_INIT_SIZE;
    return 0;
}

int StackEmpty(SqStack *s){
    if(s->base == s->top){
        return 0;
    }else{
        return -1;
    }
}

int Push(SqStack *s, int *e){
    if((s->top-s->base) >= s->stacksize){
        s->base = (int*)realloc(s->base, (s->stacksize+STACK_INCREMENT)*(sizeof(int)));
        if(!s->base){
            return -1;
        }
        s->top = s->base + s->stacksize;
        s->stacksize += STACK_INCREMENT;
    }
    if(e == NULL){
        return -1;
    }else{
        *s->top = *e;
    }
    s->top += 1;
    return 0;
}

int Pop(SqStack *s, int *e)
{
    if(s->top == s->base) {
        return -1;
    }else{
        s->top -=1;
        *e = *s->top;
        return 0;
    }
}

 

代码运行

/home/lady/CLionProjects/untitled/cmake-build-debug/untitled
开始创建一个有向图,请输入顶点数，弧数:9,11
输入第1个顶点: V1
输入第2个顶点: V2
输入第3个顶点: V3
输入第4个顶点: V4
输入第5个顶点: V5
输入第6个顶点: V6
输入第7个顶点: V7
输入第8个顶点: V8
输入第9个顶点: V9
输入第1条弧(顶点1, 顶点2, 权值): V1,V2,6
输入第2条弧(顶点1, 顶点2, 权值): V1,V3,4
输入第3条弧(顶点1, 顶点2, 权值): V1,V4,5
输入第4条弧(顶点1, 顶点2, 权值): V2,V5,1
输入第5条弧(顶点1, 顶点2, 权值): V3,V5,1
输入第6条弧(顶点1, 顶点2, 权值): V4,V6,2
输入第7条弧(顶点1, 顶点2, 权值): V5,V7,9
输入第8条弧(顶点1, 顶点2, 权值): V5,V8,7
输入第9条弧(顶点1, 顶点2, 权值): V6,V8,4
输入第10条弧(顶点1, 顶点2, 权值): V7,V9,2
输入第11条弧(顶点1, 顶点2, 权值): V8,V9,4

类型：有向网；顶点数 9, 弧数 11
邻接表:
(0,V1)    (3,V4) 5    (2,V3) 4    (1,V2) 6    
(1,V2)    (4,V5) 1    
(2,V3)    (4,V5) 1    
(3,V4)    (5,V6) 2    
(4,V5)    (7,V8) 7    (6,V7) 9    
(5,V6)    (7,V8) 4    
(6,V7)    (8,V9) 2    
(7,V8)    (8,V9) 4    
(8,V9)    
逆邻接表:
(0,V1)    
(1,V2)    (0,V1) 6    
(2,V3)    (0,V1) 4    
(3,V4)    (0,V1) 5    
(4,V5)    (2,V3) 1    (1,V2) 1    
(5,V6)    (3,V4) 2    
(6,V7)    (4,V5) 9    
(7,V8)    (5,V6) 4    (4,V5) 7    
(8,V9)    (7,V8) 4    (6,V7) 2    

对各个顶点求入度...
(0,V1)的入度为0
(1,V2)的入度为1
(2,V3)的入度为1
(3,V4)的入度为1
(4,V5)的入度为2
(5,V6)的入度为1
(6,V7)的入度为1
(7,V8)的入度为2
(8,V9)的入度为2

进行拓扑排序:(0,V1)    (1,V2)    (2,V3)    (4,V5)    (6,V7)    (3,V4)    (5,V6)    (7,V8)    (8,V9)    

输出各个顶点的最早发生时间ve和最晚发生时间vl
ve(0,V1)=0    vl(0,V1)=0
ve(1,V2)=6    vl(1,V2)=6
ve(2,V3)=4    vl(2,V3)=6
ve(3,V4)=5    vl(3,V4)=8
ve(4,V5)=7    vl(4,V5)=7
ve(5,V6)=7    vl(5,V6)=10
ve(6,V7)=16    vl(6,V7)=16
ve(7,V8)=14    vl(7,V8)=14
ve(8,V9)=18    vl(8,V9)=18

输出各活动的最早发生时间ee和最晚发生时间el, *表示该活动为关键路径
(0,V1)->(3,V4), weight:5, ee=0, el=3, tag= 
(0,V1)->(2,V3), weight:4, ee=0, el=2, tag= 
(0,V1)->(1,V2), weight:6, ee=0, el=0, tag=*
(1,V2)->(4,V5), weight:1, ee=6, el=6, tag=*
(2,V3)->(4,V5), weight:1, ee=4, el=6, tag= 
(3,V4)->(5,V6), weight:2, ee=5, el=8, tag= 
(4,V5)->(7,V8), weight:7, ee=7, el=7, tag=*
(4,V5)->(6,V7), weight:9, ee=7, el=7, tag=*
(5,V6)->(7,V8), weight:4, ee=7, el=10, tag= 
(6,V7)->(8,V9), weight:2, ee=16, el=16, tag=*
(7,V8)->(8,V9), weight:4, ee=14, el=14, tag=*

Process finished with exit code 0

 

/home/lady/CLionProjects/untitled/cmake-build-debug/untitled
开始创建一个有向图,请输入顶点数，弧数:6,8
输入第1个顶点: V1
输入第2个顶点: V2
输入第3个顶点: V3
输入第4个顶点: V4
输入第5个顶点: V5
输入第6个顶点: V6
输入第1条弧(顶点1, 顶点2, 权值): V1,V2,3
输入第2条弧(顶点1, 顶点2, 权值): V1,V3,2
输入第3条弧(顶点1, 顶点2, 权值): V2,V4,2
输入第4条弧(顶点1, 顶点2, 权值): V2,V5,3
输入第5条弧(顶点1, 顶点2, 权值): V3,V4,4
输入第6条弧(顶点1, 顶点2, 权值): V3,V6,3
输入第7条弧(顶点1, 顶点2, 权值): V4,V6,2
输入第8条弧(顶点1, 顶点2, 权值): V5,V6,1

类型：有向网；顶点数 6, 弧数 8
邻接表:
(0,V1)    (2,V3) 2    (1,V2) 3    
(1,V2)    (4,V5) 3    (3,V4) 2    
(2,V3)    (5,V6) 3    (3,V4) 4    
(3,V4)    (5,V6) 2    
(4,V5)    (5,V6) 1    
(5,V6)    
逆邻接表:
(0,V1)    
(1,V2)    (0,V1) 3    
(2,V3)    (0,V1) 2    
(3,V4)    (2,V3) 4    (1,V2) 2    
(4,V5)    (1,V2) 3    
(5,V6)    (4,V5) 1    (3,V4) 2    (2,V3) 3    

对各个顶点求入度...
(0,V1)的入度为0
(1,V2)的入度为1
(2,V3)的入度为1
(3,V4)的入度为2
(4,V5)的入度为1
(5,V6)的入度为3

进行拓扑排序:(0,V1)    (1,V2)    (4,V5)    (2,V3)    (3,V4)    (5,V6)    

输出各个顶点的最早发生时间ve和最晚发生时间vl
ve(0,V1)=0    vl(0,V1)=0
ve(1,V2)=3    vl(1,V2)=4
ve(2,V3)=2    vl(2,V3)=2
ve(3,V4)=6    vl(3,V4)=6
ve(4,V5)=6    vl(4,V5)=7
ve(5,V6)=8    vl(5,V6)=8

输出各活动的最早发生时间ee和最晚发生时间el, *表示该活动为关键路径
(0,V1)->(2,V3), weight:2, ee=0, el=0, tag=*
(0,V1)->(1,V2), weight:3, ee=0, el=1, tag= 
(1,V2)->(4,V5), weight:3, ee=3, el=4, tag= 
(1,V2)->(3,V4), weight:2, ee=3, el=4, tag= 
(2,V3)->(5,V6), weight:3, ee=2, el=5, tag= 
(2,V3)->(3,V4), weight:4, ee=2, el=2, tag=*
(3,V4)->(5,V6), weight:2, ee=6, el=6, tag=*
(4,V5)->(5,V6), weight:1, ee=6, el=7, tag= 

Process finished with exit code 0